目录
一、理论基础
二、MATLAB仿真程序
三、仿真结果
一、理论基础
地图和机器人的模型如下:
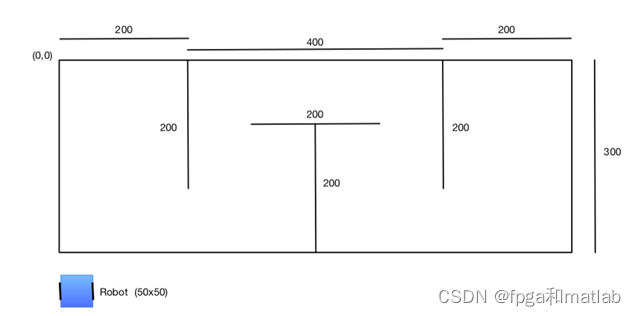
1.使用一个2*2的网格大小(gridsize)和5度的角分辨率(angular resolution),创建机器人的构型空间(Configurationspace)。请简单说明,并输出构型空间的视图。
机器人的初始状态:坐标(0,45),90度
2.使用谈心搜索算法计算从(50,50)到(750, 250)的最短路径。请在图中标明并且输出最短路径的长度。
3.使用中轴变换计算最安全的路径(最安全的路径是指离墙最远的路径)。请在图中标明并且输出最短路径的长度。
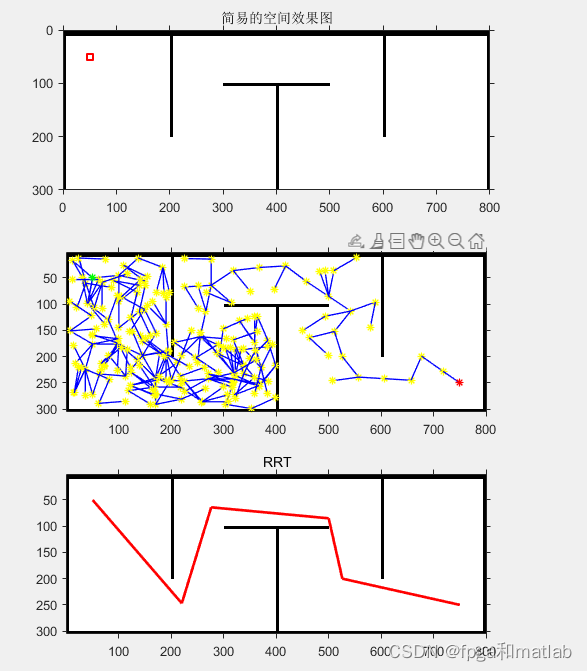
4.使用PRM(probabilistic roadmaps)算法计算从(50,50)到(750, 250)的最短路径。分别使用50、100、500个样本点。请在图中标明并输出这些路径的长度。
使用一个2*2的网格大小(grid size)和5度的角分辨率(angular resolution),创建机器人的构型空间(Configuration space)。请简单说明,并输出构型空间的视图。
机器人的初始状态:坐标(0,45),90度
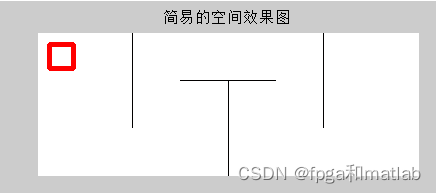
这里,如果按1*1的方格,算法将及其复杂,数据量极大,我们这里将网格进行分割。300*800的空间,分割为10*10一个方格。
PRM算法是通过对空间进行大量采样来构建路线图,用于后续的特定查询。路线图是无向连接图,车辆或机器人可以路线图上由任意一点移动到其他点。点与点连接线最简单的就是直线。路线图构建好之后可以采用经典的A*算法来搜索路径。PRM算法构建路线图过程如下所示。

二、MATLAB仿真程序
clc;clear;close all;warning off;addpath 'func\'%转弯分辨率ang = 5/180*pi;W = 800;H = 300;K = 10;Scale = max(W,H)/K;[MAPs,Start,Ends,cc,MAPpoint] = func_wall(Scale,K);%显示方格场景图func_Map2fig(MAPs,Start,Ends,H/K,W,H,K);S1 = Start;S2 = 0;S3 = inf;S4 = [];S5 = [];Paths = ['R','L','D','U'];%开始贪心算法搜索,while ~max(ismember(S1,Ends))&&~isempty(S1) [temp,kj] = min(S2+S3); %搜索路径值用来判断往哪走 [path1,path2,path3] = func_search(S1(kj),S2(kj),MAPs,Ends); S4 = [S4;S1(kj)]; S5 = [S5;S2(kj)]; %判决 if kj>1&&kj<length(S1) S1=[S1(1:kj-1);S1(kj+1:end)]; S2=[S2(1:kj-1);S2(kj+1:end)]; S3=[S3(1:kj-1);S3(kj+1:end)]; else S1=[S1(kj+1:end)]; S2=[S2(kj+1:end)]; S3=[S3(kj+1:end)]; end for jj=1:length(path3) if ~isinf(path1(jj)) if ~max([S1;S4]==path3(jj)) MAPpoint{path3(jj)}=Paths(jj); S1 = [S1; path3(jj)]; S2 = [S2; path1(jj)]; S3 = [S3; path2(jj)]; elseif max(S1==path3(jj)) i=find(S1==path3(jj)); if S2(i)>path1(jj) S2(i)=path1(jj); S3(i)=path2(jj); MAPpoint{S1(i)}=Paths(jj); end else i=find(S4==path3(jj)); if S5(i)>path1(jj) S5(i)=path1(jj); MAPpoint{S4(i)}=Paths(jj); end end end end if isempty(S1) break; endendPathss=func_check(Ends,MAPpoint); figure(1);plot(Pathss(:,1)+0.5,Pathss(:,2)+0.5-(W-H)/K,'color',[0 1 0],'LineWidth',2);title('贪婪算法');X=Pathss(:,1)+0.5;Y=Pathss(:,2)+0.5-(W-H)/K;%输出长度d=0;for i = 1:length(X)-1 d = d+K*sqrt((X(i)-X(i+1))^2 + (Y(i)-Y(i+1))^2);endd
三、仿真结果
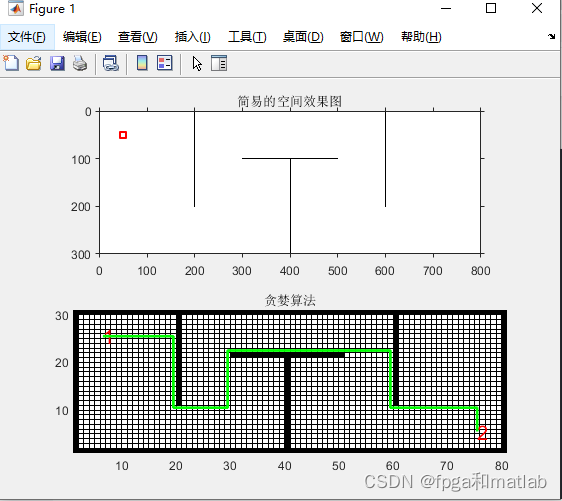
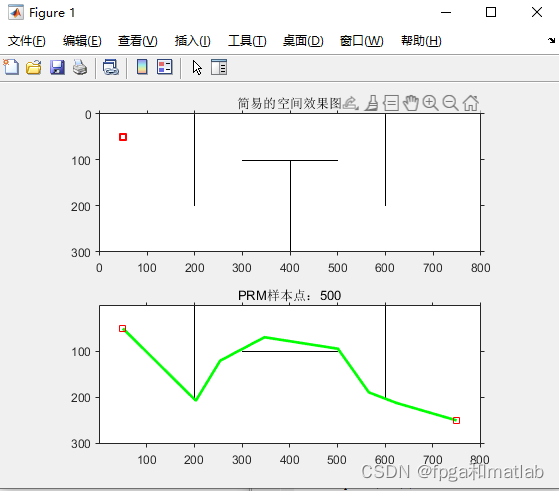
A16-73