题目回顾与写在前面
首先,我们队在历经了千辛万苦之后,光荣得获得了 省三......队伍构成 物理*2 + 计算机*1队伍分工 计算机-->受力分析 物理-->数值计算总评:图一乐,狠乐!物理系,计算机系嘛,不怎么看建模的啦! 如果只是考虑力学问题的话,我们分析得肯定还不太到位,但是这个题肯定很好分析所以,这个题主要在数值计算上 |
 |
 |
思路
 |
基本假设
1.海水是无粘及无旋的。
2.浮子在线性周期微幅波作用下会受到波浪激励力(矩)、附加惯性力(矩)、兴波阻尼力(矩)和静水恢复力(矩)。
3.忽略中轴、底座、隔层及 PTO的质量和各种摩擦。
4.初始浮子和振子平衡于静水中。
问题一的求解

|
|
| 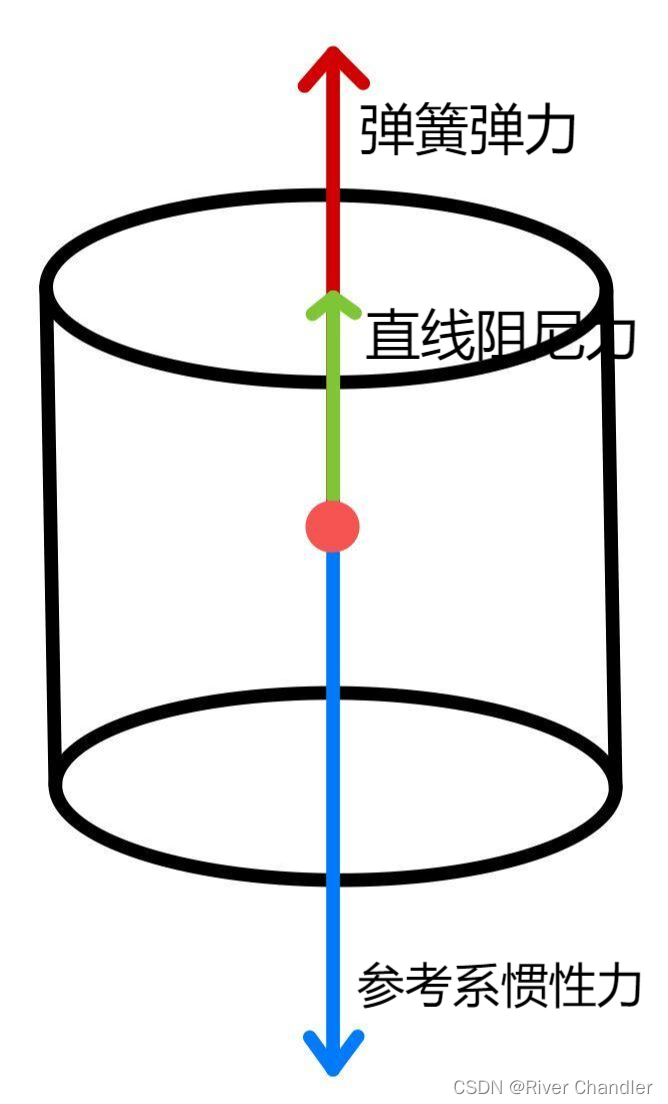 |
| 问题一浮子振子整体的受力分析 | 问题一振子在浮子参考系下的受力分析 |
数值求解
4级显式Runge-Kutta方法
|
|
求解过程的代码:
import numpy as npimport matplotlib.pyplot as pltfrom matplotlib.animation import FuncAnimationimport matplotlibmatplotlib.rcParams["font.sans-serif"] = ["SimHei"]matplotlib.rcParams["axes.unicode_minus"] = Falsedef runge_kutta4(df, a, b, h, y0): num = len(y0) x = np.arange(a, b+h, h) w = np.zeros( (x.size, num) ) w[0, :] = y0 for i in range(x.size - 1): s0 = df(x[i], w[i, :],i*h) s1 = df(x[i] + h/2., w[i, :] + h * s0 / 2.,i*h) s2 = df(x[i] + h/2., w[i, :] + h * s1 / 2.,i*h) s3 = df(x[i+1], w[i, :] + h * s2,i*h) w[i+1,:] = w[i,:] + h * (s0 + 2*(s1+s2) + s3) / 6. return x, wdef df(x, variables,i): th1, th2, om1, om2 = variables A = np.zeros((2, 2)) b = np.zeros(2) A[0, 0] = 2433+6201.535 A[0, 1] = 2433 A[1, 0] = 2433 A[1, 1] = 2433 b[0] = 6250*np.cos(1.4005*i)-10045*4*np.arctan(1)*th1*(th1<=0.999989731)-10045*4*np.arctan(1)*0.999989731*(th1>0.999989731)-656.3616*om1 b[1] = -80000*th2-10000*om2 dom1, dom2 = np.linalg.solve(A,b) return np.array([om1,om2,dom1,dom2])a, b = 0.0,180.0h = 0.01th10 = 0.1th20 = 0.1om10 = 0.1om20 = 0.1y0 = np.array([th10, th20, om10, om20])# 计算求解t, w = runge_kutta4(df, a, b, h, y0)th1 = w[:, 0]th2 = w[:, 1]om1 = w[:, 2]om2 = w[:, 3]plt.plot([h*i for i in range(len(th1))],th1,label="x1")plt.plot([h*i for i in range(len(th2))],th2,label="x2")#plt.plot([i*h for i in range(len(om1))],om1,label="x1'")#plt.plot([i*h for i in range(len(om2))],om2,label="x2'")plt.xlabel("时间/s")plt.ylabel("位移/m",rotation=True)#plt.ylabel("速度/m*s^-1",rotation=True)plt.legend()plt.title("x1 x2 随时间的变化量;求解步长 -m1"+str(h))plt.savefig("x1 x2 随时间的变化量 求解步长 -m1"+str(h)+".jpg")plt.show()#plt.title("x1' x2' 随时间的变化量;求解步长 "+str(h))#plt.savefig("x1' x2' 随时间的变化量 求解步长 "+str(h)+".jpg")#plt.show()import xlsxwriter as xls#th1 = np.array(th1[::20])#th2 = np.array(th2[::20])#om1 = np.array(om1[::20])#om2 = np.array(om2[::20])th1 = np.array(th1)th2 = np.array(th2)om1 = np.array(om1)om2 = np.array(om2)workbook = xls.Workbook("1-1-000-m1.xlsx")worksheet = workbook.add_worksheet("Sheet1")headings = ["x1","x2","v1","v2"]worksheet.write_row("A1",headings)worksheet.write_column("A2",th1)worksheet.write_column("B2",om1)worksheet.write_column("C2",th1+th2)worksheet.write_column("D2",om1+om2)workbook.close()问题二

变步长搜索法

矩形法数值积分
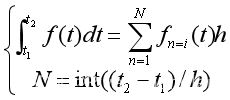
问题二解法
| 60秒-80秒 | 80秒-100秒 | 100秒-120秒 |
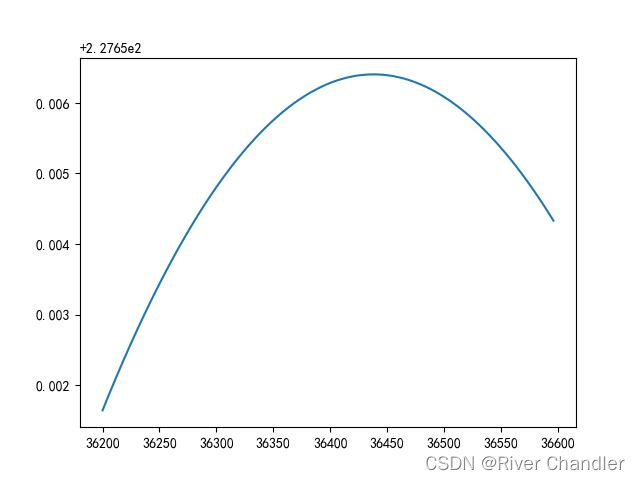
|  |  |
 |  |  |
| 最大平均功率/瓦特 | |||||
| 290.141018 | 282.3656312 | 285.2766 | 289.2045 | 291.1627 | 291.2182 |
| Beta值 | |||||
| 38130 | 37850 | 37940 | 37970 | 37970 | 37970 |
| Alpha值 | |||||
| 0.098 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
问题三

数值解(类似一,二的解法)
| 物理量 \ 时间 | 10s | 20s | 40s | 60s | 100s |
| 浮子垂荡位移 | -0.685529938 | -0.604544566 | 0.195435534 | -0.156064651 | 0.142943636 |
| 浮子垂荡速度 | 0.5487404 | -0.698097309 | 0.922311628 | -0.867269801 | -0.917710776 |
| 浮子纵摇角位移 | 0.0293679 | 0.001331413 | -0.000590353 | -0.002998229 | -0.015015832 |
| 浮子纵摇角速度 | -0.115251745 | 0.020961283 | -0.03312735 | 0.042788285 | 0.051748796 |
| 振子垂荡位移 | -0.764772476 | -0.657517866 | 0.199876278 | -0.159952226 | 0.168056577 |
| 振子垂荡速度 | 0.565213931 | -0.788403868 | 1.017008287 | -0.952503212 | -0.997533033 |
| 振子纵摇角位移 | 0.030535835 | 0.001439153 | -0.000618481 | -0.003153401 | -0.015074399 |
| 振子纵摇角速度 | -0.117325818 | 0.019228743 | -0.031151057 | 0.046614327 | 0.056193417 |
问题四
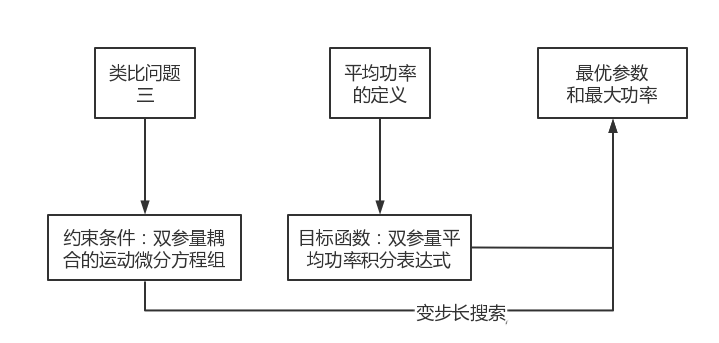
我们的优化模型:


