文章目录

前言神经网络公式推导参数定义前向传播（forward）反向传播（backward）隐藏层和输出层的权重更新输入层和隐藏层的权重更新 代码实现python手写实现pytorch实现 总结参考

前言

因为要课上讲这东西，因此总结总结，发个博客

神经网络公式推导

参数定义

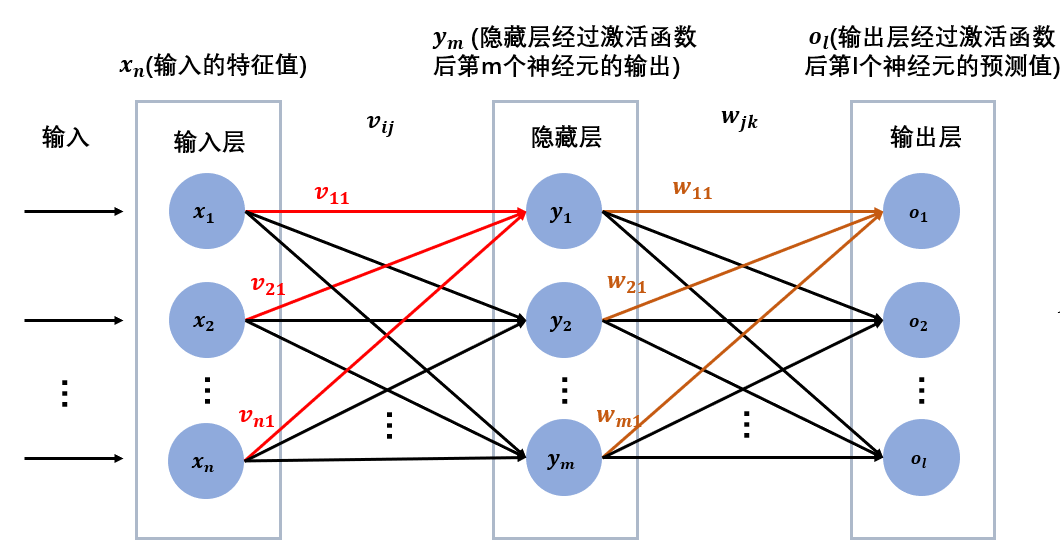
模型图

假设我们有这么一个神经网络，由输入层、一层隐藏层、输出层构成。
（这里为了方便，不考虑偏置bias）
输入特征为xn
输入层与隐藏层连接的权重为vij
隐藏层的输出（经过激活函数）为ym
隐藏层与输出层连接的权重为wjk
输出层的预测值（经过激活函数）为ol
隐藏层和输出层后面都接sigmoid激活函数。
Simoid激活函数如下：

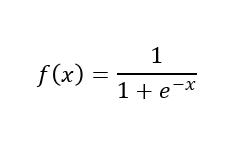
前向传播（forward）

首先，我们可以试着表示一下y1
如模型图所示可以表示为：

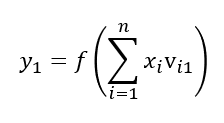
那么我要表示yj呢？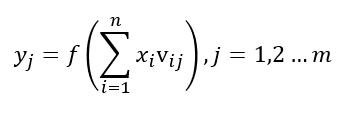

其中j=1时，就是y1的表示，j=m时，就是ym的表示。

同理我们可以得到：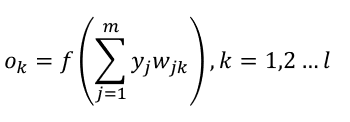

ok表示输出层第k个神经元的预测值，这就是我们需要的输出。
至此，正向传播完毕。

反向传播（backward）

光正向传播，我们只能得到模型的预测值，不能更新模型的参数，也就是说，正向传播的时候，模型是不会被更新的。

因为我们得到了模型输出的预测值，并且我们手上有对应的真实值，我们就能够将误差反向传播，更新模型参数。

具体操作怎么操作呢？

首先，我们需要定义误差，即预测值和真实值差了多少，以此来决定模型参数更新的方向和力度。

这里我们采用简单的差的平方的损失函数：

注意，这里只是更新输出层第k个神经元所反馈的误差。

隐藏层和输出层的权重更新

首先根据已知如下：

输出层预测值ok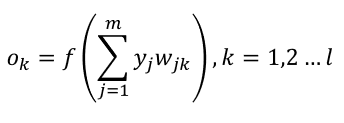

激活函数Sigmoid

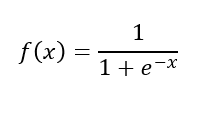
那我们可以试着展开一下Ek

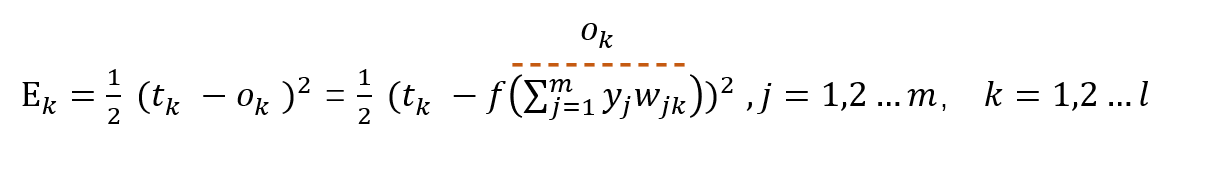
因为我们现在需要更新的是wjk，因此展开到wjk我们就能有一个比较形象的认识了。

根据梯度下降法可得，我们现在只需要求出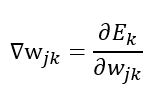

即可通过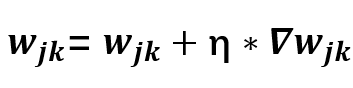

来更新我们隐藏层和输出层的权重了。
那么如何计算呢？
直接求导可能有点混乱，利用复合函数求导的方法，我们可以根据链式法则将表达式展开如下：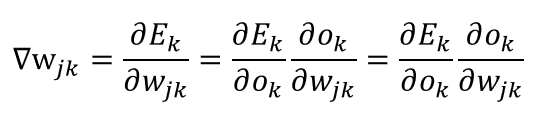

接下来我们分别求出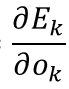

以及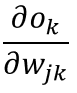

就可以了。

我们先给出激活函数的导数推导过程：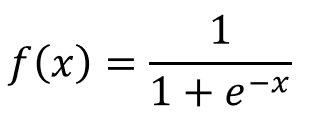


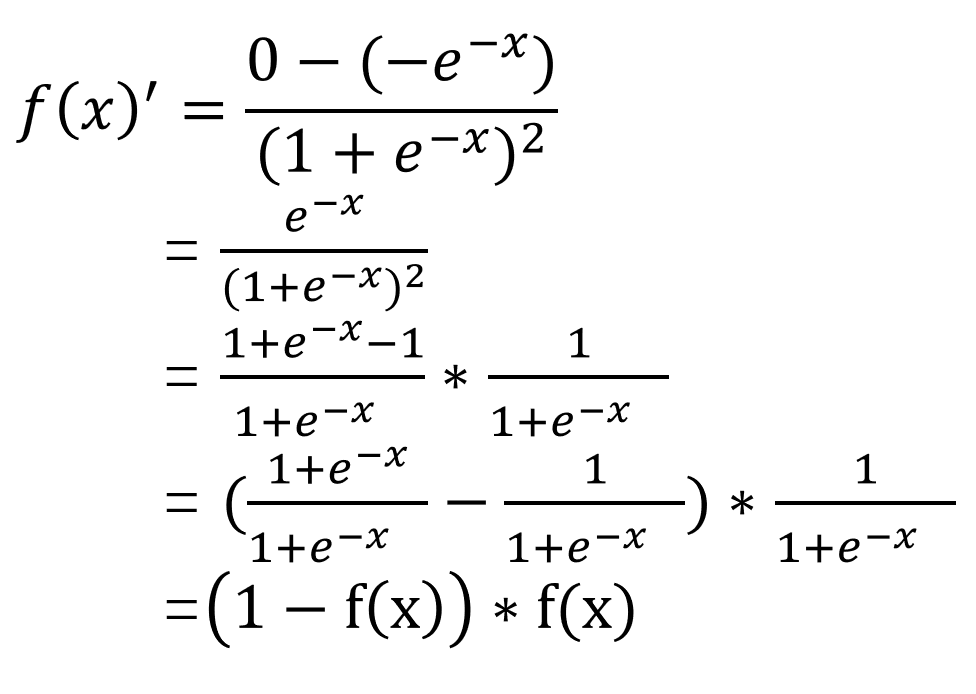
就是使用复合函数除的求导法则进行求导。我们可以发现sigmoid函数求导之后还是挺好看的。

接下来就是计算两个导数即可。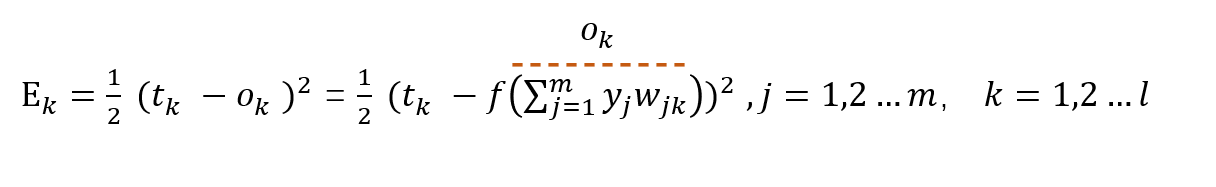

首先：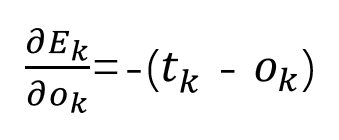

一眼就能看出来了吧。

这个可能会有点困难，但是仔细看看，发现还是很简单的。
首先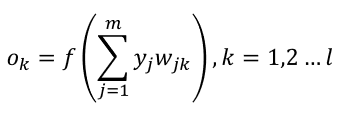

然后我们知道 [f(g(x))]’ = g(x)’ * f(g(x))’
例如 y = log(x^2)
那么 y’ = (x^2)’ * [log(x^2)]’ = 2*x * 1 / x^2 = 2x / x^2
由于这里f(x)是Sigmoid激活函数
f(x)’ = (1-f(x)) * f(x) （上面已经推到过了）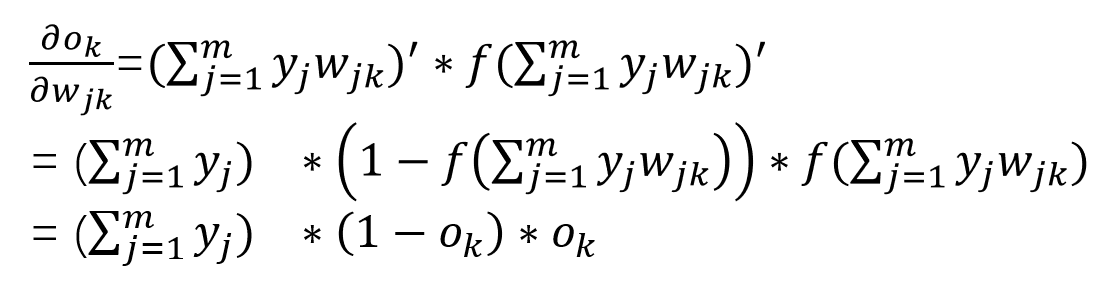

那么这个结果计算起来就比较简单了。

既然如此，将结果拼起来就是我们要求的结果了：

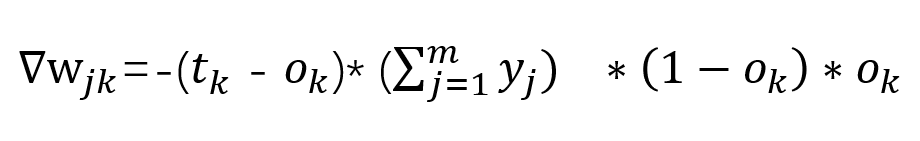
其中：

全是已知的，不就可以更新参数了嘛

因此，加个学习率这层权重更新推导就大功告成了。

输入层和隐藏层的权重更新

如果上面的推导看懂了，下面的推导就非常简单了，无非就是多展开一级，多求一次导数而已。

首先（前面已经推到过了）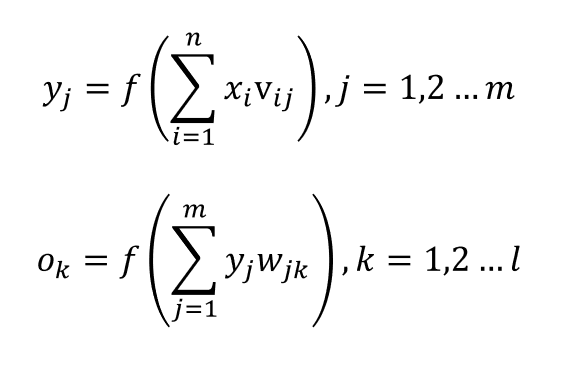

那么我们可以将误差再展开一级：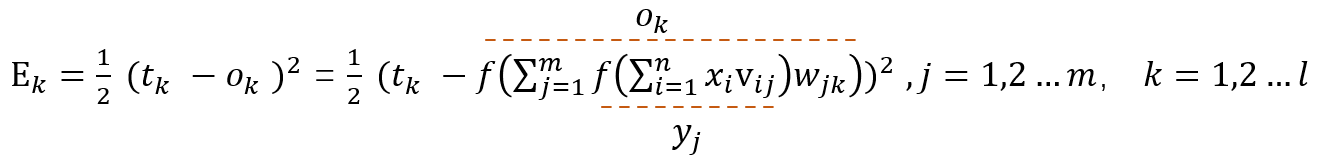

那么下面这个就非常值观了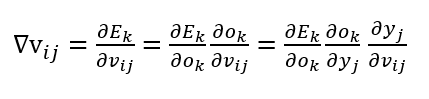

同样的，我们也分别求出三次的导数，最后拼起来就行了。

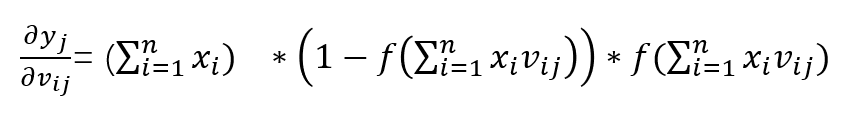
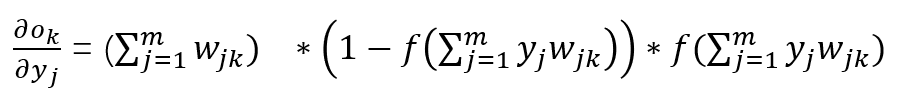
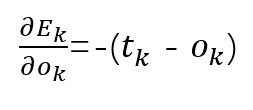
至此分别求出来了，拼起来就是我们要的结果了：

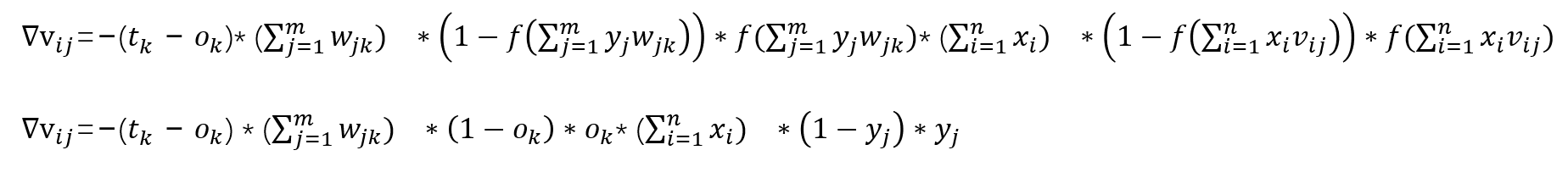
通过观察，里面全是已知的变量
那么更新公式也就有了：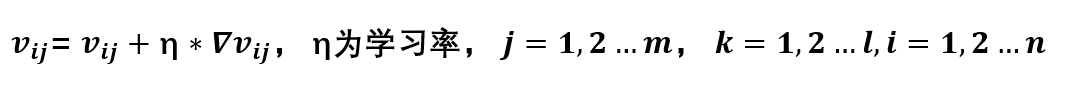

至此我们公式推导就完成了。

代码实现

首先需要数据集，这里使用手写数据集。
训练集 http://www.pjreddie.com/media/files/mnist_train.csv
测试集 http://www.pjreddie.com/media/files/mnist_test.csv

python手写实现

其中比较关键的就是那两个参数的更新公式。

隐藏层和输出层的权重更新：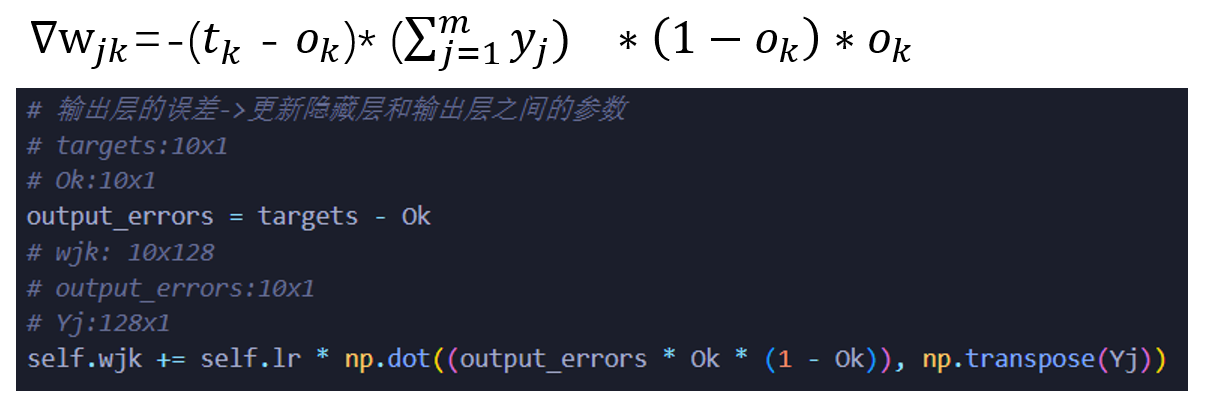

输入层和隐藏层的权重更新

完整代码如下：

import numpy as npimport scipy.specialimport matplotlib.pyplotclass Network:    def __init__(self, input_size, hidden_size, output_size, learning_rate):        self.input_size = input_size        self.hidden_size = hidden_size        self.output_size= output_size        self.lr = learning_rate                # 初始化参数        # 输入层和隐藏层之间的参数        self.Vij = np.random.normal(0.0, pow(self.hidden_size, -0.5), (self.hidden_size, self.input_size))        # 隐藏层和输出层之间的参数        self.wjk = np.random.normal(0.0, pow(self.output_size, -0.5), (self.output_size, self.hidden_size))                # sigmoid激活函数        self.activation_function = lambda x: 1 / (1 + np.exp(-x))                    def train(self, inputs_list, targets_list):        # 数据        inputs = np.array(inputs_list, ndmin=2).T        # 标签        targets = np.array(targets_list, ndmin=2).T                # 隐藏层的输入        hidden_inputs = np.dot(self.Vij, inputs)        # 隐藏层的输出        Yj = self.activation_function(hidden_inputs)                # 输出层的输入        final_inputs = np.dot(self.wjk, Yj)        # 输出层的输出        Ok = self.activation_function(final_inputs)                # 输出层的误差->更新隐藏层和输出层之间的参数        # targets:10x1          # Ok:10x1        output_errors = targets - Ok         # wjk: 10x128         # output_errors:10x1        # Yj:128x1        self.wjk += self.lr * np.dot((output_errors * Ok * (1 - Ok)), np.transpose(Yj))                # 隐藏层的误差->输入层和隐藏层之间的参数        # wjk: 10x128         # output_errors:10x1        hidden_errors = np.dot(self.wjk.T, output_errors * (1 - Ok) * Ok) # wjk: 10x128 output_errors:10x1        # Vij:128x784        # hidden_errors: 128x1        # Yj:128x1        # inputs:784x1        self.Vij += self.lr * np.dot((hidden_errors * Yj * (1 - Yj)), np.transpose(inputs))                 # 简单计算均方误差        errors = (np.power(output_errors, 2).sum() + np.power(hidden_errors, 2).sum())        return errors    def predict(self, inputs_list):        inputs = np.array(inputs_list, ndmin=2).T        hidden_inputs = np.dot(self.Vij, inputs)        Yj = self.activation_function(hidden_inputs)                final_inputs = np.dot(self.wjk, Yj)        Ok = self.activation_function(final_inputs)                return Ok    def get_acc(self, data):                sum = len(data)        true_n = 0        for d in data:            all_values = d.split(',')            inputs = (np.asfarray(all_values[1:])/255.0 * 0.99) + 0.01            pred = np.argmax(self.predict(inputs))            if int(pred) == int(all_values[0]):                true_n += 1        return true_n / sum            input_size = 784hidden_size = 128output_size = 10learning_rate = 0.001epoch = 2model = Network(input_size=input_size, hidden_size=hidden_size, output_size=output_size, learning_rate=learning_rate)training_data_file = open("mnist_train.csv", "r")training_data_list = training_data_file.readlines()training_data_file.closetesting_data_file = open("mnist_test.csv", "r")testing_data_list = testing_data_file.readlines()testing_data_file.closefor i in range(epoch):    errors = []    for record in training_data_list:        all_values = record.split(',')        # 输入数据        inputs = (np.asfarray(all_values[1:])/255.0 * 0.99) + 0.01        # 标签数据        targets = np.zeros(output_size) + 0.01        targets[int(all_values[0])] = 0.99        # 训练        train_errors = model.train(inputs, targets)        errors.append(train_errors)    print("epoch", i)    print("训练集平均损失为", np.mean(errors))train_acc = model.get_acc(training_data_list)test_acc = model.get_acc(testing_data_list)print("训练集准确率", train_acc)print("测试集准确率", test_acc)

输出：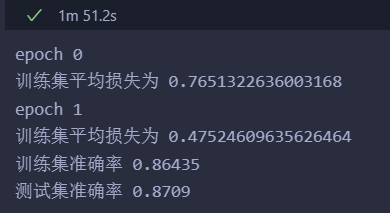

pytorch实现

import pandas as pdimport numpy as npimport torch as thimport torch.nn as nnimport torch.utils.data.dataloader as dataloaderfrom torch.utils.data import TensorDatasetfrom tqdm import tqdmfrom sklearn.metrics import accuracy_scoredef get_dataloader(batch_size, file_name):    filedata = pd.read_csv(file_name, header=None)    label = filedata.values[:, 0]    data = filedata.values[:, 1:]    data = th.from_numpy(data).to(th.float32)    label = th.from_numpy(label).to(th.long)  # 标签这里用不到，但是不影响吧    dataset = TensorDataset(data, label)    data_loader = dataloader.DataLoader(dataset=dataset, shuffle=True, batch_size=batch_size)      return data_loaderbatch_size = 256input_size = 784hidden_size = 128output_size = 10learning_rate = 0.001epoch = 2test_loader = get_dataloader(batch_size=batch_size, file_name = "mnist_test.csv")train_loader = get_dataloader(batch_size=batch_size, file_name = "mnist_train.csv")class network(nn.Module):    def __init__(self, input_size, hidden_size, output_size):        super().__init__()        self.input_size = input_size        self.hidden_size = hidden_size        self.output_size = output_size        self.w1 = nn.Linear(input_size, hidden_size, bias=False)        self.w2 = nn.Linear(hidden_size, output_size, bias=False)        self.sigmoid = nn.Sigmoid()            def forward(self, x):        i2h = self.w1(x)        i2h = self.sigmoid(i2h)        h2o = self.w2(i2h)        h2o = self.sigmoid(h2o)        return h2odef evaluate_model(model, iterator, criterion):    all_pred = []    all_y = []    losses = []    for i, batch in tqdm(enumerate(iterator)):        if th.cuda.is_available():            input = batch[0].cuda()            label = batch[1].type(th.cuda.LongTensor)        else:            input = batch[0]            label = batch[1]                y_pred = model(input)        loss = criterion(y_pred, label)        losses.append(loss.cpu().detach().numpy())        predicted = th.max(y_pred.cpu().data, 1)[1]        all_pred.extend(predicted.numpy())        all_y.extend(label.cpu().detach().numpy())    score = accuracy_score(all_y, np.array(all_pred).flatten())    return score, np.mean(losses)model = network(input_size=input_size, hidden_size=hidden_size, output_size=output_size)optimizer = th.optim.Adam(model.parameters(), lr=learning_rate) # Adam优化器loss_func = nn.CrossEntropyLoss() # 损失函数train_scores = []test_scores = []train_losses = []test_losses = []for epoch in range(epoch):    model.train() # 模型训练    for step, (x, label) in enumerate(train_loader):        pred = model(x)        loss = loss_func(pred, label)      # 损失函数        optimizer.zero_grad()               # 清空梯度        loss.backward()                     # 反向传播        optimizer.step()                    # 优化器    model.eval() # 固定参数    train_score, train_loss = evaluate_model(model, train_loader, loss_func)    test_score, test_loss = evaluate_model(model, test_loader, loss_func)    train_losses.append(train_loss)    test_losses.append(test_loss)    train_scores.append(train_score)    test_scores.append(test_score)    print('#' * 20)    print('train_acc:{:.4f}'.format(train_score))    print('test_acc:{:.4f}'.format(test_score))    import matplotlib.pyplot as plt# 训练完画图x = [i for i in range(len(train_scores))]fig = plt.figure()plt.plot(x, train_scores, color ="r", label="train_score")plt.plot(x, test_scores, color="g", label="test_score")plt.legend()plt.show()# 训练完画图x = [i for i in range(len(train_scores))]fig = plt.figure()plt.plot(x, train_losses, color ="r", label="train_loss")plt.plot(x, test_losses, color="g", label="test_loss")plt.legend()plt.show()

输出

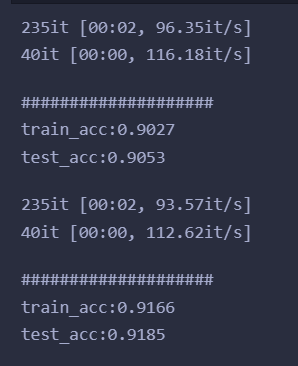
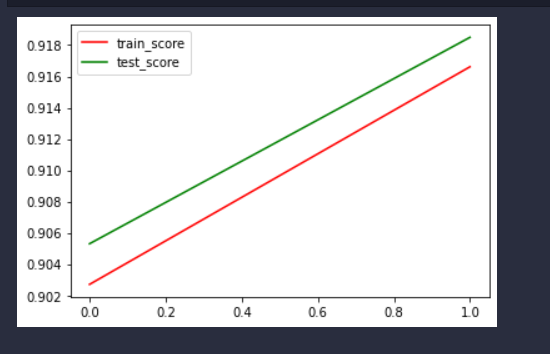
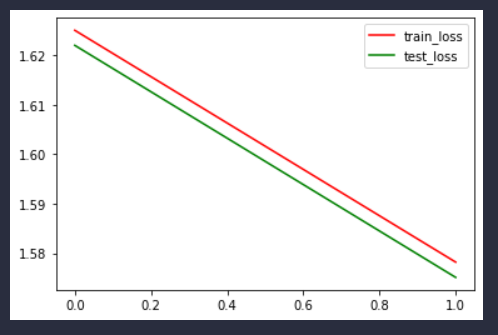
总结

感觉从推导到代码实现也是一个反复的过程，从推导发现代码写错了，写不出代码了就要去看看推导的过程，这个过程让我对反向传播有了较全面的理解。

我们发现，手写代码运行时间要一分多钟而pytorch其实只要10s不到，毕竟框架，底层优化很多，用起来肯定用框架。

以及二者准确率有一些差距，可能是因为pytorch里使用了交叉熵损失函数，比较适合分类任务；手写的并没有分batch，而是所有数据直接更新参数，但是pytorch里分了batch，分batch能够使得模型训练速度加快（并行允许），也使得模型参数更新的比较平稳。

参考

神经网络反向传播算法及代码实现