二叉树中查找后继节点问题
作者:Grey
原文地址:
博客园:二叉树中查找后继节点问题
CSDN:二叉树中查找后继节点问题
题目描述
给定一个二叉查找树,以及一个节点,求该节点在中序遍历的后继,如果没有则返回 null
题目链接见:LintCode 448 · Inorder Successor in BST
思路一,利用中序遍历递归解法,使用 List 收集中序遍历的节点,然后遍历一遍 List,找到给定节点的下一个节点即可,中序遍历的递归方法代码很简单,参考二叉树的先,中,后序遍历(递归,非递归)。
完整代码如下
public class Solution { public static TreeNode inorderSuccessor(TreeNode root, TreeNode p) { List<TreeNode> ans = new ArrayList<>(); if (root == null) { return null; } in2(root, ans); boolean find = false; for (TreeNode c : ans) { if (c == p) { find = true; } else if (find) { return c; } } return null; } private static void in2(TreeNode root, List<TreeNode> ans) { if (root == null) { return; } in2(root.left, ans); ans.add(root); in2(root.right, ans); }}时间复杂度 O(N),空间复杂度 O(N)。
同样,中序遍历可以使用迭代方法来写,思路和递归方法一样,标记遍历到的节点 p,然后设置已遍历的标志位,如果标志位设置过,则下一个遍历到的元素就是后继节点。
完整代码如下,核心就是把中序遍历的递归解改成迭代
public class Solution { public TreeNode inorderSuccessor(TreeNode root, TreeNode p) { if (root == null) { return null; } boolean flag = false; Stack<TreeNode> stack = new Stack<>(); TreeNode cur = root; while (!stack.isEmpty() || cur != null) { if (cur != null) { stack.push(cur); cur = cur.left; } else { cur = stack.pop(); if (cur == p) { // 遍历到当前位置,记录一下 flag = true; } else if (flag) { // 下一次遍历的位置,就是后继节点 return cur; } cur = cur.right; } } return null; }}思路二,使用 Morris 遍历实现中序遍历,这样可以让空间复杂度达到 O(1),时间复杂度依旧 O(N)。Morris 遍历的内容参考:Morris 遍历实现二叉树的遍历。完整代码如下
public class Solution { public TreeNode inorderSuccessor(TreeNode head, TreeNode p) { if (head == null) { return null; } TreeNode ans = null; TreeNode cur = head; TreeNode mostRight; boolean find = false; while (cur != null) { mostRight = cur.left; if (mostRight != null) { while (mostRight.right != null && mostRight.right != cur) { mostRight = mostRight.right; } if (mostRight.right == null) { mostRight.right = cur; cur = cur.left; continue; } else { mostRight.right = null; } } if (find) { ans = cur; find = false; } if (cur == p) { find = true; } cur = cur.right; } return ans; }}思路三,
利用二叉搜索树的特性,如果目标节点的右孩子不为空,则目标节点右树最左节点就是目标节点的后继节点,示例如下
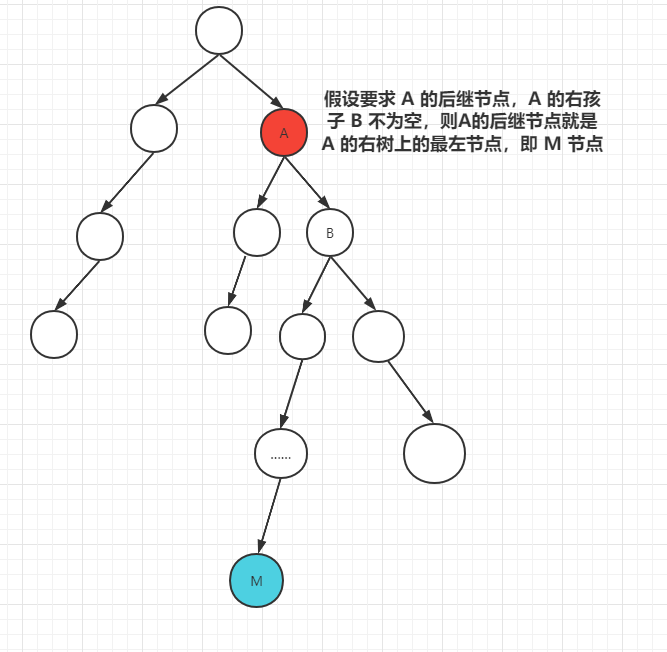
如果目标节点右孩子为空,则只需要找第一个大于目标节点值的节点即可,根据二叉搜索树的性质,每个节点的右孩子都比当前节点值大,每个节点的左孩子都比当前节点值小。
在遍历过程中,
如果当前节点的值大于目标节点的值,则先记录下当前节点(有可能是备选答案,但是不确定有没有更接近目标值的选择),然后遍历的节点往左边移动,
如果当前节点的值小于目标节点的值,一定不是后继,遍历的节点往右边移动。
如果当前节点的值等于目标节点的值,说明一定找到了后继(因为这个过程中可以确定当前节点没有右孩子,所以,到这一步,肯定是通过后继过来的,或者后继为 null),直接 break 即可。
空间复杂度O(1),时间复杂度O(h),其中 h 为二叉树的高度。
完整代码如下
public class Solution { public static TreeNode inorderSuccessor(TreeNode root, TreeNode p) { if (p == null) { return null; } if (p.right != null) { return rightLeftMost(p.right); } TreeNode successor = null; while (root != null) { if (root.val > p.val) { successor = root; root = root.left; } else if (root.val < p.val) { root = root.right; } else { break; } } return successor; } private static TreeNode rightLeftMost(TreeNode p) { while (p.left != null) { p = p.left; } return p; }}更多
算法和数据结构笔记