目录
编辑
前言
正文
基本步骤
案例:换酒问题
题目
示例 1
示例 2
分析
代码
总结
前言
Greedy algorithm,又称贪婪算法,其所求即在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的算法。
本文将快速带你入门贪心算法。
例如在旅行推销员问题中,如果旅行员每次都选择最近的城市,那这就是一种贪心算法。
贪心算法在有最优子结构的问题中尤为有效。最优子结构的意思是局部最优解能决定全局最优解。简单地说,问题能够分解成子问题来解决,子问题的最优解能递推到最终问题的最优解。
贪心算法与动态规划的不同在于它对每个子问题的解决方案都做出选择,不能回退。动态规划则会保存以前的运算结果,并根据以前的结果对当前进行选择,有回退功能。
在应用中贪心法可以解决一些最优化问题,如:求图中的最小生成树、求哈夫曼编码……
对于其它问题,贪心法一般不能得到我们所要求的答案。一旦一个问题可以通过贪心法来解决,那么贪心法一般就是解决这个问题的最好办法。
由于贪心法的高效性以及其所求得的答案比较接近最优结果,贪心法也可以用作辅助算法或者直接解决一些要求结果不特别精确的问题。在不同情况,选择最优的解,可能会导致辛普森悖论(Simpson's Paradox),不一定出现最优的解。
正文
基本步骤
步骤 1:从某个初始解出发;
步骤 2:采用迭代的过程,当可以向目标前进一步时,就根据局部最优策略,得到一部分解,缩小问题规模;
步骤 3:将所有解综合起来。
案例:换酒问题
题目
小区便利店正在促销,用 numExchange 个空酒瓶可以兑换一瓶新酒。你购入了 numBottles 瓶酒;如果喝掉了酒瓶中的酒,那么酒瓶就会变成空的。请计算出最多能喝到多少瓶酒。
示例 1
输入:numBottles = 9, numExchange = 3 输出:13 解释:你可以用 3 个空酒瓶兑换 1 瓶酒。所以最多能喝到 9 + 3 + 1 = 13 瓶酒。
示例 2
输入:numBottles = 15, numExchange = 4 输出:19 解释:你可以用 4 个空酒瓶兑换 1 瓶酒。所以最多能喝到 15 + 3 + 1 = 19 瓶酒。
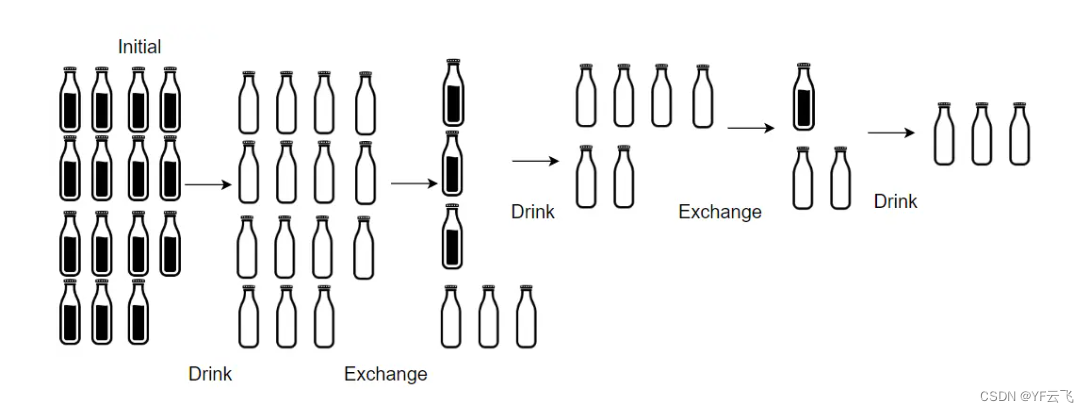
分析
这道题贪心的维度非常明显,直接暴露在题目表面。
即当前喝完所有饮料后变为空瓶加上已有空瓶后,最大限度的、贪心的兑换饮料,依次类推,直到手上的空瓶不足以兑换出一瓶饮料止。
代码
class Solution(object): def numWaterBottles(self, numBottles, numExchange): """ :type numBottles: int :type numExchange: int :rtype: int """ sumb = numBottles empty = numBottles while empty // numExchange: bottle = empty // numExchange # 兑酒数 empty = bottle + empty % numExchange # 空瓶子数 sumb += bottle return sumb总结
所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,所做出的仅是在某种意义上的局部最优解。
贪心算法没有固定的算法框架,算法设计的关键是贪心策略的选择,贪心策略使用的前提是局部最优能导致全局最优。
必须注意的是,贪心算法不是对所有问题都能得到整体最优解,选择的贪心策略必须具备无后效性,即某个状态以后的过程不会影响以前的状态,只与当前状态有关(区别于动态规划)。所以对所采用的贪心策略一定要仔细分析其是否满足无后效性。
