一、01背包问题详解
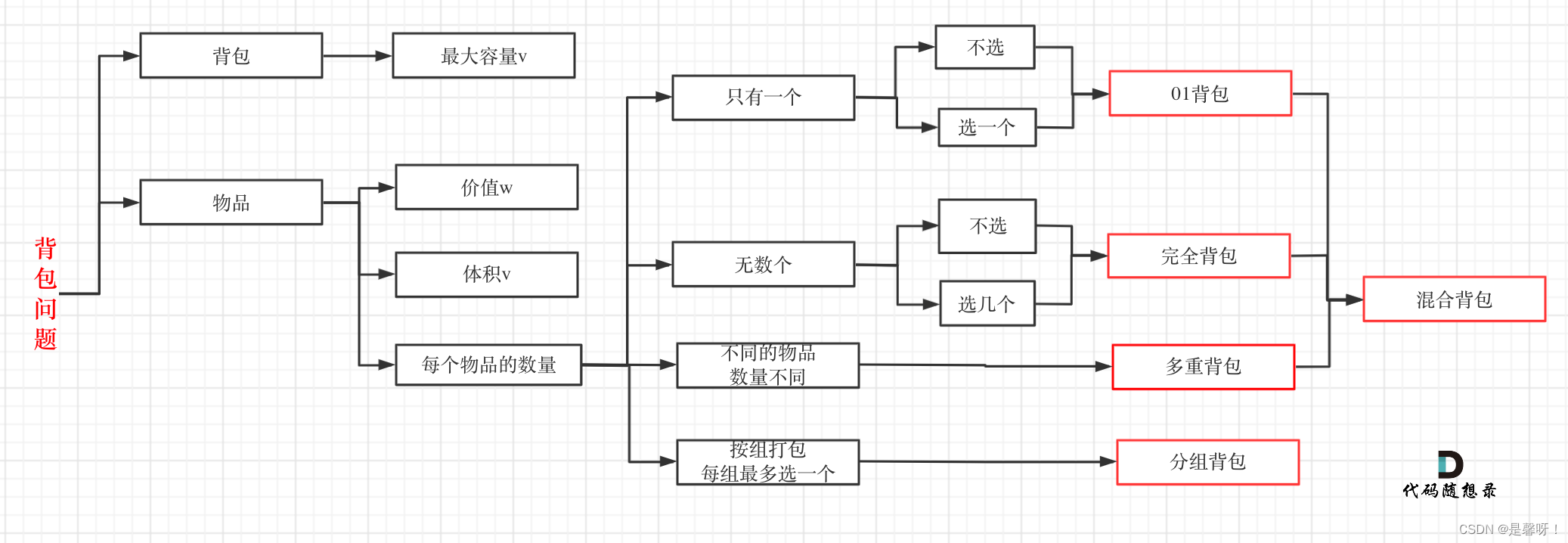
使用二维数组 dp[i] [j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。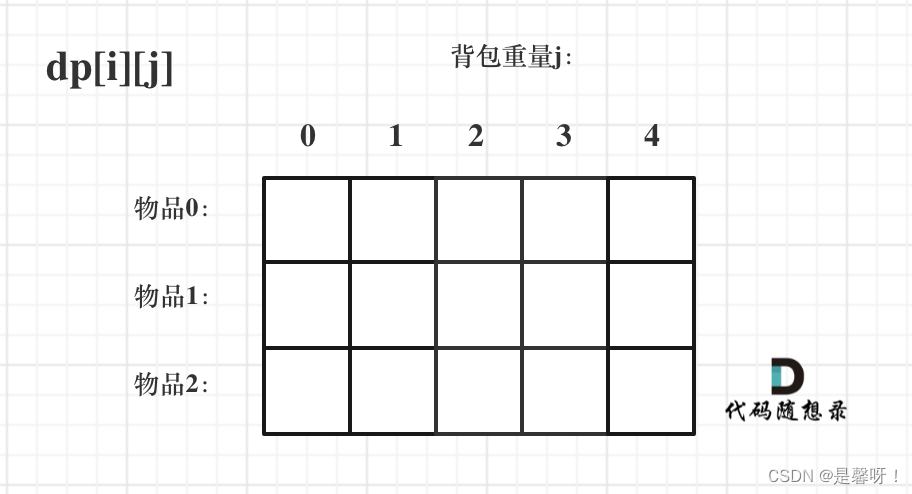
确定递推公式
dp数组的初始化
首先从dp[i][j] 的定义出发,如果背包容量j为0的话,即dp [i] [0] ,无论是选取哪些物品,背包价值总和一定为0。如图: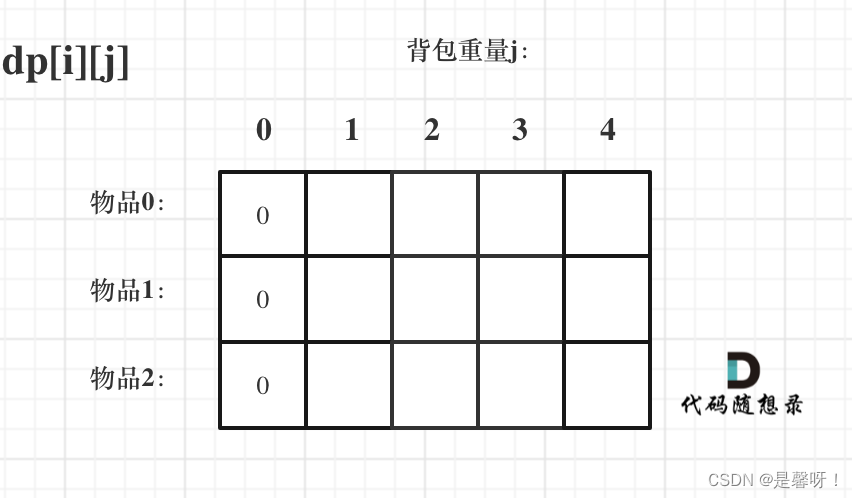
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。 dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。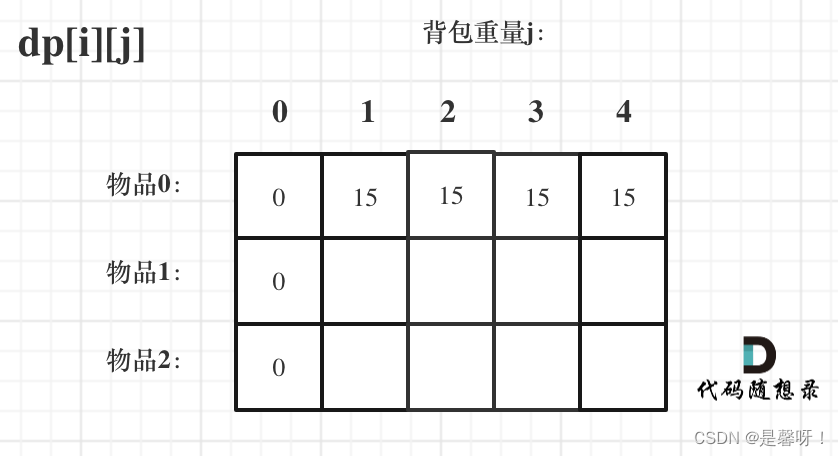
function testWeightBagProblem (weight, value, size) { // 定义 dp 数组,物品的数量为行,背包的不同容量为列(注意由于可以不放,所以是size+1) const dp = Array(weight.length).fill().map(() => Array(size + 1).fill(0)); // 初始化,对于物品0,放入不同容量背包的最大价值 // j就代表不同的容量,最大为背包的最大容量。 for(let j = weight[0]; j <= size; j++) { dp[0][j] = value[0]; } // 对于每个物品,放入不同的背包里的最大价值。 // 由于上面已经把物品0的可能性列出了,所以这里从物品1开始 for(let i = 1; i < weight.length; i++) { // 不同的背包容量,从0开始 for(let j = 0; j <= size; j++) { // 如果背包的容量不能放下物品,此时的最大价值就是上一个状态的 if(j < weight[i]) dp[i][j] = dp[i - 1][j]; // 否则就是比较放入物品i 和 不放入物品的i 这两种情况的最大价值 else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); } } return dp[len - 1][size];}function test () { console.log(testWeightBagProblem([1, 3, 4, 5], [15, 20, 30, 55], 6));}test();二、有关题目
416. 分割等和子集
题目链接
转换问题
这道题可以换一种表述:给定一个只包含正整数的非空数组 nums,判断是否可以从数组中选出一些数字,使得这些数字的和等于整个数组的元素和的一半。因此这个问题可以转换成「0-1背包问题」。
背包就是整个数组的元素和的一半,物品就是数组。需要从数组中取任意个数字,使得和等于指定数
判断不可能的情况
(1) nums的总和sum为奇数,则不可以对分,为false
(2) 目标值targetSum (即背包重量是 nums总和sum的一半) 小于nums数组中的最大值,为false
dp数组,n行targetSum+1 列,即构造上面的方格
dp[i][j] 表示从数组的 [0,i]下标范围内选取若干个正整数(可以是 0 个),是否存在一种选取方案使得被选取的正整数的和等于 j。初始时,dp 中的全部元素都是 false。
初始化,即边界情况
dp[0][0] = true, 不选即满
dp[i][0] = true, i >= 1; 表示容量为0,有1个及以上个物品时可认为不选即满,固可以填满
dp[0][i] = false, i >= 1; 即初始的值。表示容量 大于等于 1时,没有物品可选则无法填满
递推公式
var canPartition = function(nums) { let n = nums.length // 两个子集的和等于总和的一半,所以如果总和为奇数,那么就是false let sum = 0 for(const s of nums){ sum += s } if(sum % 2 != 0) return false // 目标和,即背包容量 const targetSum = sum / 2 // 如果有物品的重量大于目标和,则为fasle if(Math.max(...nums) > targetSum) return false // 转换为01背包问题,即从nums(物品)里选择出的数字等于targetSum(背包的容量) // 1、dp数组,初始化全为false let dp = new Array(n).fill().map(() => new Array(targetSum+1).fill(false)) // 2、初始化,dp[i][0] = true for(let i=0; i<n; i++){ dp[i][0] = true } dp[0][nums[0]] = true // 状态更新 for(let i = 1; i < n; i++) { for(let j = 1; j <= targetSum; j++) { if(j < nums[i]) dp[i][j] = dp[i - 1][j]; else dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]]; } } return dp[n-1][targetSum]};494. 目标和
题目链接
在这里插入代码片