现代检测技术课程实验编程：最小二乘法应用编程

一、最小二乘法编程题目描述二、最小二乘法编程题目要求三、什么是最小二乘法四、最小二乘法编程步骤4.1、 界面的设计4.2、 程序的编写4.2.1、程序在计算按钮如下的回调函数中编写4.2.2、编辑的文本框输入的数据转换成数字类型的数据4.2.3、将Xi、Yi数据存放与数组中4.2.4、计算最小二乘法直线拟合的回归参数a、b4.2.5、计算五条直线的残差平方和4.2.6、判断最佳的最小二乘法直线的拟合4.2.7、数据和图像的显示 五、最小二乘法编程总结

一、最小二乘法编程题目描述

最小二乘法编程题目描述如下所示

在对量程为10MPa的压力传感器进行标定时，传感器输出电压值与压力值之间的关系如下表所示，请简述最小二乘法准则的意义，并分析下列电压-压力直线中哪一条最符合最小二乘法准则？（使用计算机辅助进行计算）

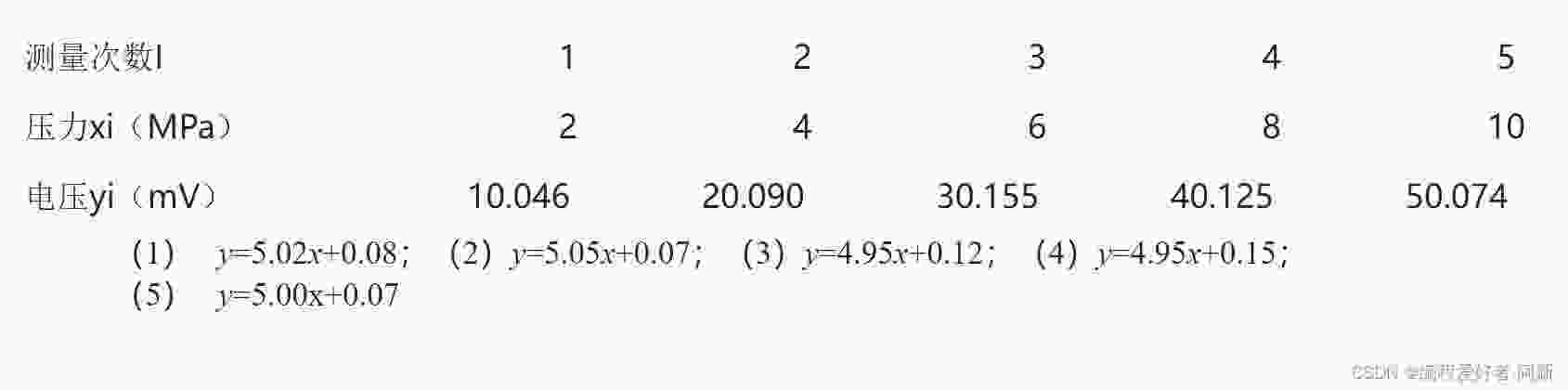
（1） y=5.02x+0.08；（2）y=5.05x+0.07；
（3） y=4.95x+0.12；（4）y=4.95x+0.15；
（5） y=5.00x+0.07

二、最小二乘法编程题目要求

最小二乘法编程题目要求如下所示

使用计算机软件（VB、VC、JAVA、LabVIEW、Matlab、Python均可）编程完成本次编程题目；

所编程序要有较为美观的GUI界面，可以通过人机界面输入校准数据xi/yi，和备选直线方程的参数。

所编程序，要能够直接显示哪条直线为最佳直线，不能人为进行判断。

对所编程序的原理和运行结果进行介绍和分析。

三、什么是最小二乘法

最小二乘法定义如下所示

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合，其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达 。最小二乘法是解决曲线拟合问题最常用的方法。

四、最小二乘法编程步骤

最小二乘法编程

4.1、 界面的设计

使用MATLAB2014b软件进行GUI页面的设计，如下图所示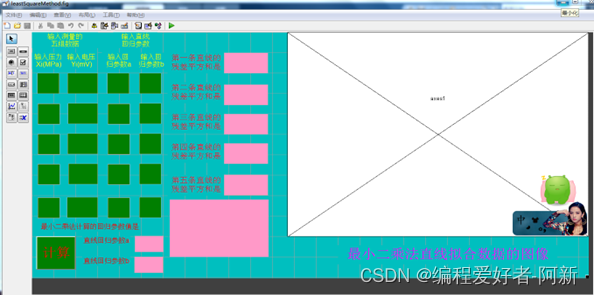

1 界面可以进行测量数据的压力和电压的输入、五条拟合直线的回归参数a、b。2 点击计算按钮，可以完成最小二乘法直线拟合的回归参数a、b。五条直线的残差平方和。自动判断哪条直线最符合最小二乘法准则。3 页面最右边的轴可以显示最小二乘法直线拟合的图像。

4.2、 程序的编写

4.2.1、程序在计算按钮如下的回调函数中编写

1 程序在计算按钮如下的回调函数中编写，代码如下

function pushbutton1_Callback(hObject, eventdata, handles)

4.2.2、编辑的文本框输入的数据转换成数字类型的数据

2 将可以编辑的文本框输入的数据转换成数字类型的数据，代码如下

Xi1 =  get(handles.edit_Xi1, 'String'); Yi1 =  get(handles.edit_Yi1, 'String');Xi2 =  get(handles.edit_Xi2, 'String'); Yi2 =  get(handles.edit_Yi2, 'String');Xi3 =  get(handles.edit_Xi3, 'String'); Yi3 =  get(handles.edit_Yi3, 'String');Xi4 =  get(handles.edit_Xi4, 'String'); Yi4 =  get(handles.edit_Yi4, 'String');Xi5 =  get(handles.edit_Xi5, 'String'); Yi5 =  get(handles.edit_Yi5, 'String'); Xi1 = str2num(Xi1); Yi1 = str2num(Yi1);Xi2 = str2num(Xi2); Yi2 = str2num(Yi2);Xi3 = str2num(Xi3); Yi3 = str2num(Yi3);Xi4 = str2num(Xi4); Yi4 = str2num(Yi4);Xi5 = str2num(Xi5); Yi5 = str2num(Yi5); a1 =  get(handles.edit_a1, 'String'); b1 =  get(handles.edit_b1, 'String');a2 =  get(handles.edit_a2, 'String'); b2 =  get(handles.edit_b2, 'String');a3 =  get(handles.edit_a3, 'String'); b3 =  get(handles.edit_b3, 'String');a4 =  get(handles.edit_a4, 'String'); b4 =  get(handles.edit_b4, 'String');a5 =  get(handles.edit_a5, 'String'); b5 =  get(handles.edit_b5, 'String'); a1 = str2num(a1); b1 = str2num(b1);a2 = str2num(a2); b2 = str2num(b2);a3 = str2num(a3); b3 = str2num(b3);a4 = str2num(a4); b4 = str2num(b4);a5 = str2num(a5); b5 = str2num(b5);

4.2.3、将Xi、Yi数据存放与数组中

3 将Xi、Yi数据存放与数组中，代码如下

Xi = [Xi1 Xi2 Xi3 Xi4 Xi5];Yi = [Yi1 Yi2 Yi3 Yi4 Yi5];

4.2.4、计算最小二乘法直线拟合的回归参数a、b

4 计算最小二乘法直线拟合的回归参数a、b，代码如下

squareXi = Xi .* Xi;squareYi = Yi .* Yi;mulXiYi = Xi .* Yi; sumXi = sum(Xi);sumYi = sum(Yi);sumSquareXi = sum(squareXi);sumSquareYi = sum(squareYi);sumMulXiYi = sum(mulXiYi); Lxx = sumSquareXi - sumXi * sumXi / 5;Lxy = sumMulXiYi - sumXi * sumYi / 5; b = Lxy / Lxx;a = sumYi / 5 - b * sumXi / 5;

4.2.5、计算五条直线的残差平方和

5 计算五条直线的残差平方和，代码如下

SubYiXi1 = Yi - (a1 + b1 * Xi);squareSubYiXi1 = SubYiXi1 .* SubYiXi1;sumSub1 = sum(squareSubYiXi1); SubYiXi2 = Yi - (a2 + b2 * Xi);squareSubYiXi2 = SubYiXi2 .* SubYiXi2;sumSub2 = sum(squareSubYiXi2); SubYiXi3 = Yi - (a3 + b3 * Xi);squareSubYiXi3 = SubYiXi3 .* SubYiXi3;sumSub3 = sum(squareSubYiXi3); SubYiXi4 = Yi - (a4 + b4 * Xi);squareSubYiXi4 = SubYiXi4 .* SubYiXi4;sumSub4 = sum(squareSubYiXi4); SubYiXi5 = Yi - (a5 + b5 * Xi);squareSubYiXi5 = SubYiXi5 .* SubYiXi5;sumSub5 = sum(squareSubYiXi5);

4.2.6、判断最佳的最小二乘法直线的拟合

6 判断最佳的最小二乘法直线的拟合，代码如下

subArrays = [sumSub1 sumSub2 sumSub3 sumSub4 sumSub5];minSub = subArrays(1);subJudge = 1;for i = 2: 5    if minSub > subArrays(i)        minSub = subArrays(i);        subJudge = i;    endend strJudge = '最符合最小二乘法准侧的直线是: 第';subJudge = num2str(subJudge);strJudge1 = '条直线';strJudge = strcat(strJudge, subJudge, strJudge1);

4.2.7、数据和图像的显示

7 数据和图像的显示，代码如下

set(handles.text_judge, 'String', num2str(strJudge)); set(handles.edit1, 'String', num2str(sumSub1));set(handles.edit2, 'String', num2str(sumSub2));set(handles.edit3, 'String', num2str(sumSub3));set(handles.edit4, 'String', num2str(sumSub4));set(handles.edit5, 'String', num2str(sumSub5)); set(handles.edit_result_a, 'String', num2str(a));set(handles.edit_result_b, 'String', num2str(b)); plot(Xi, Yi, '*');hold on y1 = a1 + b1 * Xi;axes(handles.axes1);plot(Xi, y1, 'm');hold on y2 = a2 + b2 * Xi;axes(handles.axes1);plot(Xi, y2, 'r');hold on y3 = a3 + b3 * Xi;axes(handles.axes1);plot(Xi, y3, 'y');hold on y4 = a4 + b4 * Xi;axes(handles.axes1);plot(Xi, y4, 'k');hold on y5 = a5 + b5 * Xi;axes(handles.axes1);plot(Xi, y5, 'g');hold on

三、 程序的运行结果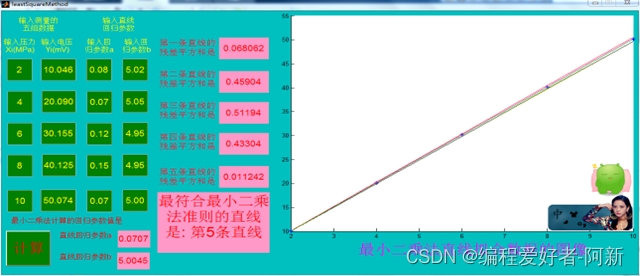

程序可以自动进行最佳拟合直线的判断。从运行的结果可以确定是第五条直线是最佳最小二乘法直线的拟合。

输入用最小二乘法计算得到的直线拟合回归参数，运行得到如下结果

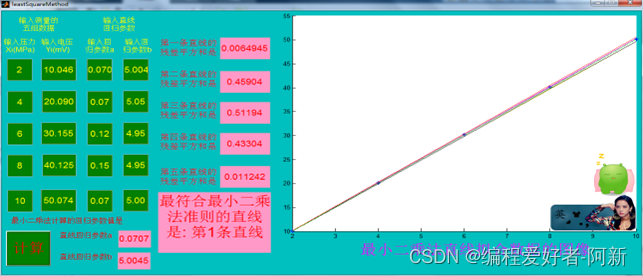
五、最小二乘法编程总结

用MATLAB所编写的GUI页面程序实现了计算最小二乘法直线拟合的回归参数的计算。自动判断哪条直线最符合最小二乘法直线拟合的准侧。最小二乘法直线拟合的图像显示。