Project 2 最后一篇,讲解 B+ 树并发控制的实现。说实话一开始博主以为这块内容不会很难(毕竟有 Project 1 一把大锁摆烂秒过的历史x),但实现起来才发现不用一把大锁真的极其痛苦,折腾了一周多才弄完。
本文分基础版算法和改进版算法两部分,基础版算法部分我就只讲实现的一些要素,改进版算法再放重要代码,避免两个版本的代码引起混乱。由于加了并发控制后代码改变的位置比较多,我这里贴的截图不能覆盖到所有,如果需要源码可以评论区或私信联系。
开始之前先推荐知乎上的两篇文章,写得都非常好,而且有带图的例子方便理解。
CMU 15445-2022 P2 B+Tree Concurrent Control
做个数据库:2022 CMU15-445 Project2 B+Tree Index
理论基础
基础版算法
首先,请把 Lecture #09: Index Concurrency Control 这个课件第 36 页开始的内容仔细看一遍,实验文档中关于并发控制的描述很简略,而这个课件中详细讲解了并发控制的基本算法和改进算法,还带了很多具体例子方便理解。这里我就简要摘抄一下核心内容。
定义 “Safe Node 安全节点”:
如果操作为插入,则没有满的节点为安全节点;如果操作为删除,则超过半满的节点为安全节点;如果操作为读取,则所有节点均为安全节点。一句话概括,就是操作时不会使树的结构发生改变的节点(插入的分裂,删除的合并)。从课件前面的例子也能看出,B+ 树实现并发访问的一个主要问题就是树的结构的改变会和读取或另一个结构改变发生冲突,造成读取无效位置或树的逻辑结构错误。而安全节点就是那些我们不用担心出现这个问题的节点。
于是,可以得出一个基础版的并发控制算法:

对于读操作,在子节点获取读锁然后把父节点的读锁释放掉;对于插入/删除操作,在子节点获取写锁,判断子节点是否安全:如果安全,将祖先节点的所有写锁释放,否则继续持有。这里也不难理解:如果子节点安全,那么对其下面的节点做插入/删除操作引起的树结构变化最多会传递到该层,而不会影响上层节点的结构,所以可以放掉祖先节点的锁允许其它操作访问。
算法的名称也非常形象:Latch Crabbing / Coupling,因为获取锁的方式就像螃蟹前进一样,先把一条腿迈到下一个位置(子节点),然后把另一条腿从上一个位置(父节点)收回来。
改进版算法
以上算法在插入/删除时第一步总是要先获得根节点的写锁(独占性),这是树形结构本身决定的,但这在性能上很容易成为瓶颈。而另一个观察是,大多数的插入/删除并不会使节点发生分裂或合并(只要节点的 max size 不设置得太小),所以实际上获取根节点(或者说那些较为靠上节点)的写锁大部分情况是不必要的。因此,课件给出了一个改进版的算法:

其思路是先 “乐观” 地假设插入/删除不会发生分裂或合并,于是只需沿路径像读取一样获取和释放读锁,然后检查叶节点:如果叶节点安全,那么假设正确,对其更新只需要叶节点的写锁;而如果不安全,说明假设错误,重新像基础版算法一样跑一遍。显然,如果上面的观察成立,那么这种算法带来的收益是会超过其代价的。
扫描(迭代器)问题
上一节我们还实现了 B+ 树的一种操作:迭代器,也就是顺序访问所有叶节点的元素。但到目前为止我们讨论的都是从根到叶路线的并发控制,那么能否直接从叶跳到下一个叶呢?答案是不可以,课件中也给出了死锁的例子。最终给出的方案是:从一个叶节点跳到下一个叶节点时,只有立刻能获取到其读锁,才可以继续,否则直接报告错误,也就是不要等待。这部分实验讲义中说明了不在评测范围之内。
基础版算法实现
回顾上一节的代码,我们已经写了一个函数 GetLeafPage() 负责从根节点搜索到值可能所在的叶节点。并发控制的主体代码应该添加到该函数中。首先定义操作的枚举类型:

Transaction
原理讲解中提到插入/删除涉及所有祖先节点的释放,这就要用到我们前面一直忽视的参数:transaction,它携带了一个数据库事务的所有信息,不过这里我们只需要关注其两个成员 std::shared_ptr<std::deque<Page *>> page_set_ 和 std::shared_ptr<std::unordered_set<page_id_t>> deleted_page_set_,分别可以记录 B+ 树查找过程中访问的页面集合和删除的页面集合。注意前者是用双端队列记录的,能维持插入的顺序,这样释放锁时也能按照从根向下的顺序,且元素为 Page *,因为我们要用 Page 类的解锁函数。删除集合当然无所谓顺序了,而且只需记录 page_id,因为最后是用 buffer_pool_manager_->DeletePage(page_id) 删除(这个与并发控制无关,单纯是上节中忘做了x)。
根节点保护
讲义中 Common Pitfalls 部分提到了课件中没讲的一个细节:根节点的保护。这里说的根节点保护不是对根节点那个 Page 的保护,而是对获取哪个 Page 是根节点,也就是 root_page_id 访问的保护(这正是 GetLeafPage() 中搜索的第一步)。于是在 BPlusTree 类中添加一个成员 ReaderWriterLatch root_latch_,每次访问前第一步先上这个锁,再进入 latch crabbing。但这个独立定义的锁如何放入 transaction 的 page_set 集合呢?我们可以规定:在 page_set 中放入一个 nullptr,表示锁定 root_latch_,在访问 page_set 解锁时只需做一个判断即可。
Unlock 和 Unpin 的顺序问题
讲义 Common Pitfalls 提到的另一个需要思考的问题,正确操作是先 Unlock 后 Unpin,因为 Unpin 后这个 Page 的 pin count 可能降为 0,buffer_pool_manager 可能会将该 Page 指针的内容改写为另一个 Page 的,导致 Unlock 错误(如果不清楚可以回看 FetchPgImp 的实现)。
安全节点判断
这里没有什么难点,按照定义写即可。唯一需要注意的是删除时对于根节点的判断,如果是叶节点只需有 1 个或以上元素,而内部节点需要有 2 个或以上,因为根据上节代码如果只有 1 个元素则应该将子节点变为新的根节点,树的高度减一。
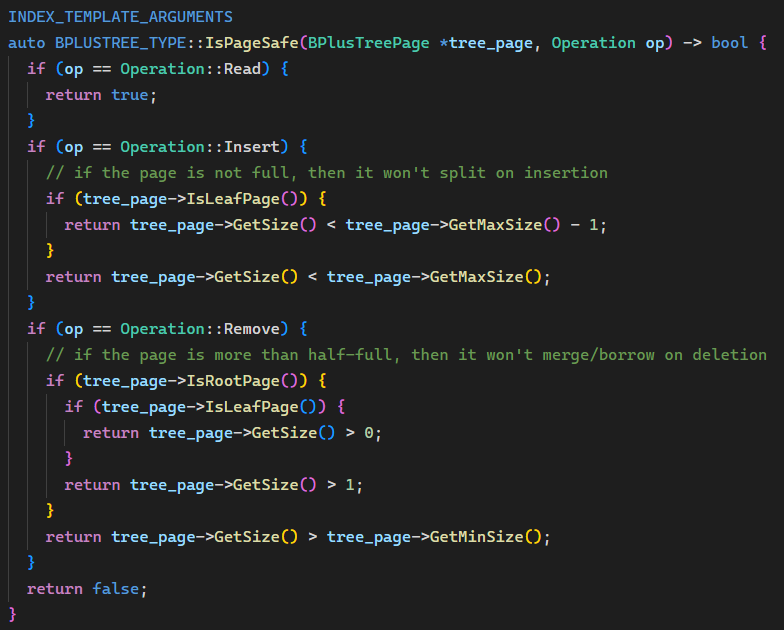
2023/03/23 更新:感谢 @weixin_45297876 的指正,这里 Remove 的判断条件应该分别为大于 1 和 2,因为 IsPageSafe() 是在执行删除前被调用的,删除后达到 0 或 1 是不安全的。
祖先节点锁释放
读锁都是获取下一层后立刻释放上一层,所以不需要用到 transaction 的 page_set 记录,只有写锁才会需要记录多个祖先节点然后一次性释放。于是可以写一个函数进行所有写锁的释放:
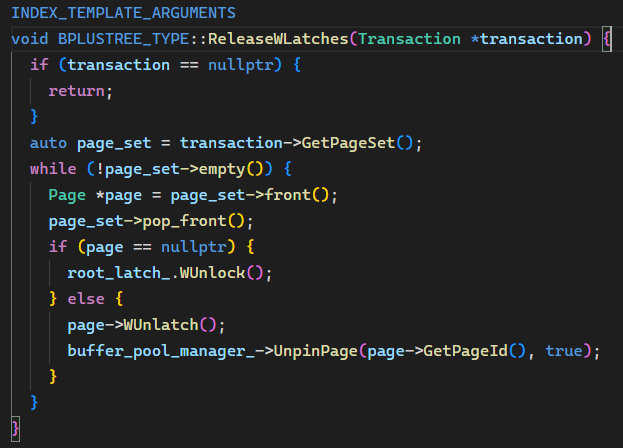
修改 GetLeafPage() 函数
刚开始应该给 root_latch_ 上读锁或写锁,但因为在调用 GetLeafPage 之前,读/插入/删除操作都需要先判断空树,所以给 root_latch_ 上锁的任务放在那些函数开头进行。因为读操作时要释放上一个节点的锁,所以添加一个 prev_page 指针,初始化为 nullptr。对于读操作,先给 root_latch_ 上读锁。每一轮中,先 page->RLatch(),然后判断 prev_page,如果是 nullptr,则将 root_latch_ RUnlock 掉;否则,将 prev_page RUnlatch 并 Unpin 掉。对于插入/删除操作,先给 root_latch_ 上写锁。每一轮中,先 page->WLatch(),然后判断当前页是否安全,如果安全,将祖先节点的写锁释放。将当前页加入到 transaction 的 page_set 中。 修改 查询/插入/删除 函数
第一步,对于读,给root_latch_ 上读锁;对于插入/删除,给 root_latch_ 上写锁,同时向 transaction 的 page_set 中添加一个 nullptr。需要想清楚的问题是:调用 GetLeafPage() 后,有哪些资源被占用(锁定),需要释放?对于读,只有叶节点被上读锁,所以最后要进行的清理是 page->RUnlatch(); buffer_pool_manager_->UnpinPage(page->GetPageId(), false);。而对于插入和删除,答案是 transaction 的 page_set 中存储的页,而前面我们已经写好了 ReleaseWLatches 函数释放这些资源,应该在所有情况 return 之前调用。对于插入,之前是每轮循环中以及最后一个循环后都把原有的页(old_tree_page)和新建的分裂页(new_tree_page)Unpin 掉,而现在可能发生分裂的节点,即那些 old_tree_page 都已记录在 transaction 的 page_set 中,它们会在最后调用 ReleaseWLatches 时被 Unpin。所以,现在只需 Unpin 所有 new_tree_page。对于删除,访问兄弟节点时要上写锁,这个是没有放在 transaction 中的。正好我们上节写过一个释放兄弟的函数 ReleaseSiblings(),所以可以把解锁放在该函数的 Unpin 之前。对于删除,在 MergePage() 中把删掉的页(即 right_page)记录到 transaction 的 deleted_page_set 中,最后记得对这个集合中的页用 buffer_pool_manager 的 DeletePage() 清理掉。 迭代器
获取迭代器前搜索位置加读锁就可以,迭代器构建时确保已获取 Page 的读锁,析构函数中解锁。在迭代器内部,需要考虑的是 operator++() 跳页时的处理。这部分讲义说了不做要求,如果想实现课件中所述 “立刻获取下一页的锁,否则不等待立刻返回失败”,需要阅读源码:Page 的锁就是一个 ReaderWriterLatch,而 ReaderWriterLatch 本质是 std::shared_mutex,只是用 RLock(),WLock() 替换了 lock_shared() 和 lock() 的名称。而 std::shared_mutex 还有一对函数:try_lock_shared() 和 try_lock(),效果正是 “尝试获取锁,立刻返回成功或失败的 bool 值”。所以,只需在 ReaderWriterLatch 和 Page 上相应添加一对 TryRLock(),TryWLock() 的包装函数即可实现。
测试
并发控制有两个可用的本地测试 b_plus_tree_concurrent_test 和 b_plus_tree_contention_test,后者会评估 B+ 树使用全局锁和你的并发控制实现的耗时比(所以如果你的 B+ 树也只用了一把大锁,这个比值应该接近 1)。正确的实现应该在 [ 2.5 , 3.5 ] [2.5, 3.5] [2.5,3.5] 这个区间内。下面是我测试我的基础版实现的结果:
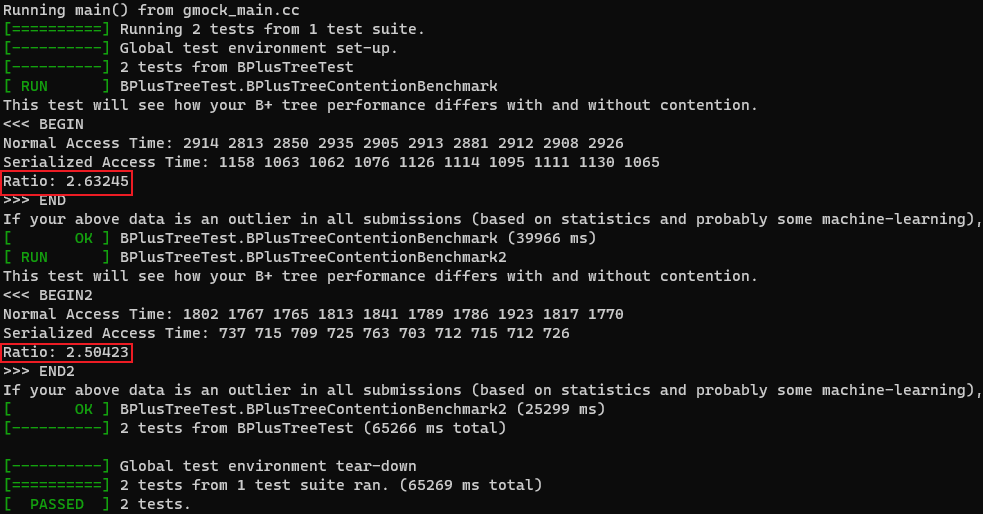
数字比较正常,但并不高。提交至 GradeScope,Leaderboard 用时为 8.74s,这个成绩emm…不太行
第一步优化
到这里博主还没确定要不要做改进版算法,就按习惯先用 gprof 跑了一下程序运行耗时统计。为了生成 gprof 统计信息,编译时要添加 -pg 参数,用 CMake 编译的添加方法为,在 bustub 目录下的 CMakeLists.txt 中,添加:
SET(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -pg")SET(CMAKE_EXE_LINKER_FLAGS "${CMAKE_EXE_LINKER_FLAGS} -pg")SET(CMAKE_SHARED_LINKER_FLAGS "${CMAKE_SHARED_LINKER_FLAGS} -pg")然后编译 b_plus_tree_contention_test,运行:
cd test./b_plus_tree_contention_test此时 test 目录中应该会生成一个 gmon.out 文件,运行:
gprof b_plus_tree_contention_test gmon.out > prof.txt打开 prof.txt,可以看到程序耗时最多的函数调用。除去一些内部函数,可以看到 BufferPoolManager 的 FetchPage 和 UnpinPage 的调用次数非常高,
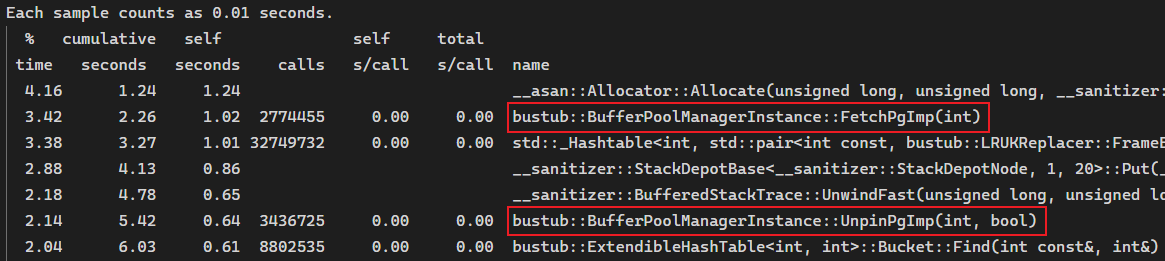
而之前参考其它博客学到了一个思路:放在 transaction 的 page_set 中的 Page 都是已经 Fetch 过的,可以直接使用,而我们的代码中有两处没有利用到这个性质,就是插入和删除中获取父节点时,都是直接 Fetch/Unpin 的,没有考虑到父节点可能已经存在于 page_set 中。于是,添加一个函数:
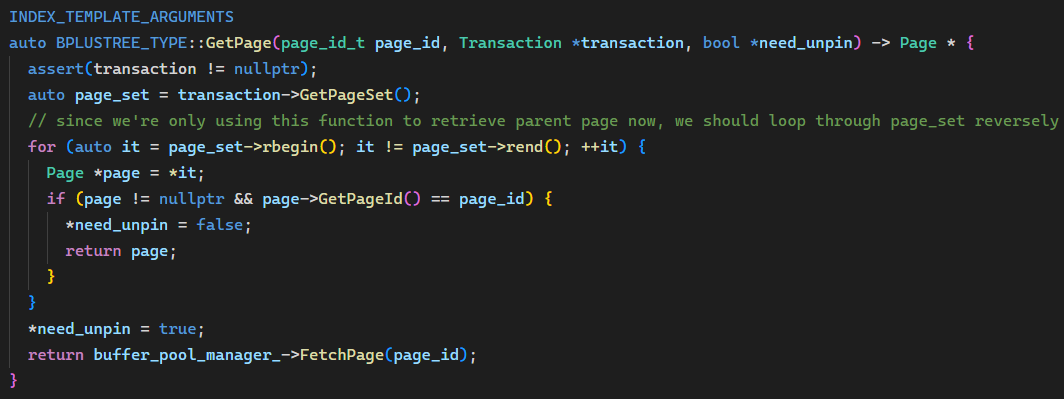
先尝试从 page_set 中获取,如果失败再 FetchPage。Insert() 中:

改了个名字,parent_tree_page 这里原来叫 parent_internal_page
删除同理。这样对 parent_page 是否需要 Unpin 要根据 parent_need_unpin 决定,如果是从 page_set 中取的则 ReleaseWLatches 中会 Unpin,不要重复。
2023/03/29 更新:感谢 @卡其大米 的提醒,因为 GetPage() 只在插入和删除获取 parent_page 这两个地方调用,parent_page 实际上肯定是在 transaction 中的(想想 safe page 的定义,能递归到该位置说明至少到这里一定不安全),所以实际上也不需要 need_unpin 判断了,写成以下形式即可:
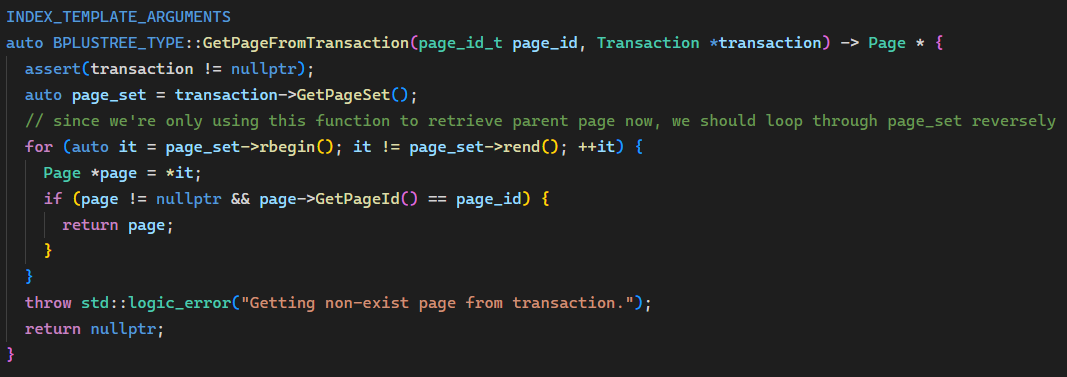
经此优化的结果如下:
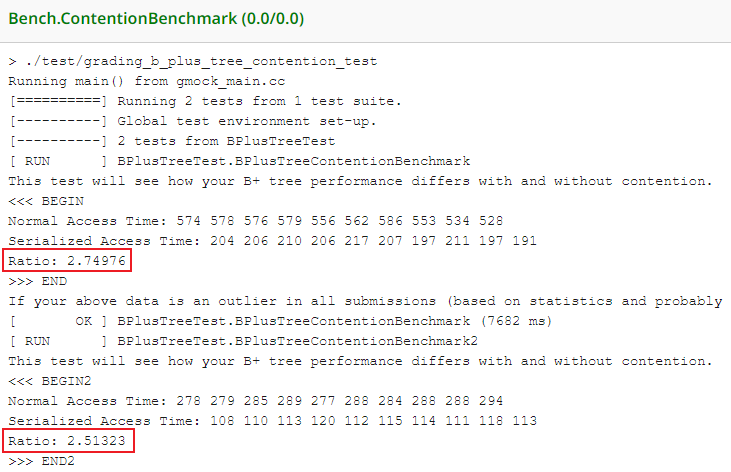
GradeScope Leaderboard 用时为 8.49s,有提升,但不多(汗)
至此博主决定还是老老实实把改进版算法实现了…
改进版算法实现
免责声明:其实博主也不确定在实现改进算法过程中有没有意外做其它可能使性能提升的操作,所以不保证实现改进算法的提升效果(x
实际上代码的更改也并不复杂,主要改 GetLeafPage() 一个函数就行。因为第二遍和第一遍搜索只是加锁的方式不一样,我们为函数添加一个 bool 参数 first_pass,默认值为 true,这样外部调用的代码都不用改。梳理一下逻辑:
root_latch_ 的读锁,从根搜索到叶节点,一路按 crabbing 的方式加锁解锁;到了叶节点,如果是读操作加读锁,如果是插入/删除操作加写锁并加入 page_set。如果叶节点不安全,将叶节点解锁,调用 GetLeafPage(..., false) 进入第二次搜索,否则直接返回叶节点。注意根据 IsPageSafe() 的实现读操作总会判定节点是安全的。进入第二次搜索,首先要获取 root_latch_ 的写锁;另外能进入第二次说明一定是插入/删除操作,直接按基础版算法处理即可。 转化为代码:
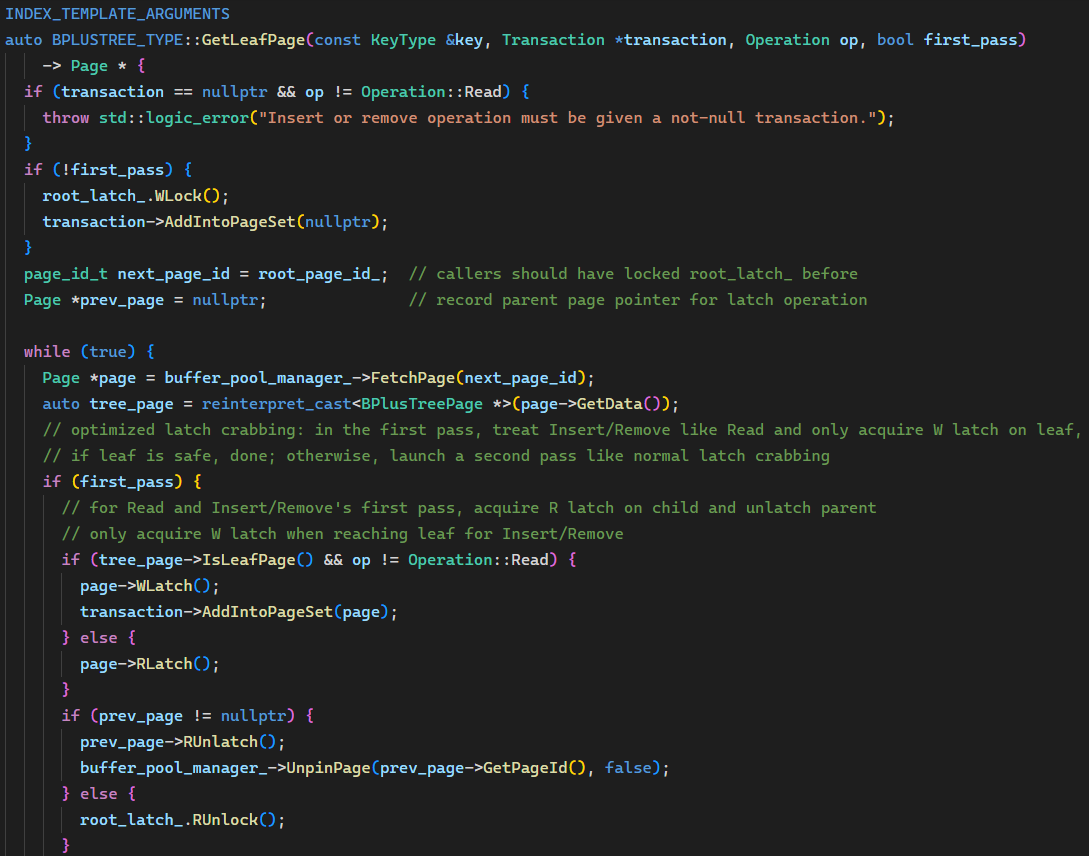
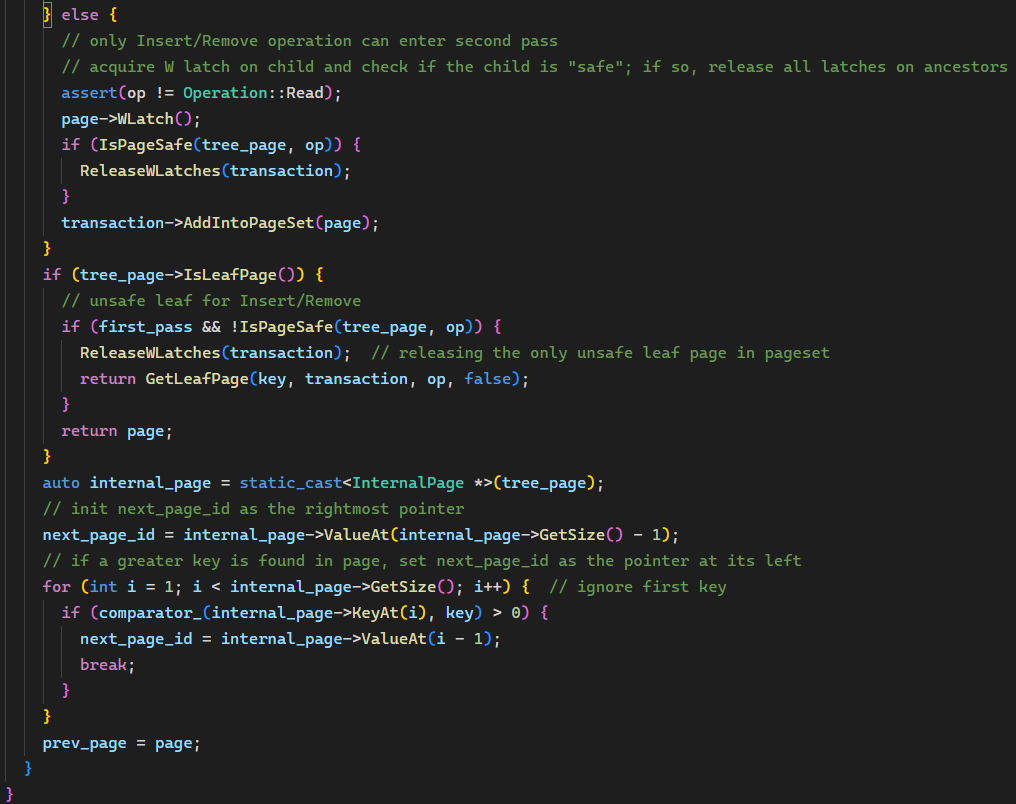
至此实现完成,进入喜闻乐见的代码大放送环节(doge),非常欢迎指出哪里还可以改进!
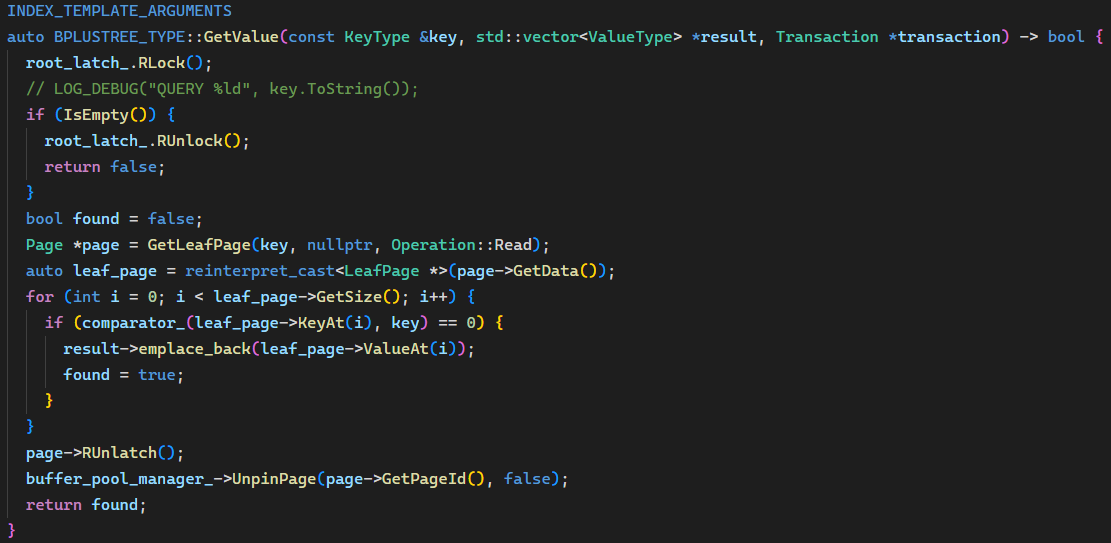
Insert() 要注意一下空树的处理,因为改为优化版后 root_latch_ 一开始加的是读锁,所以如果判定为空要新建根节点的话需要 “升级” 为写锁。然而 std::shared_mutex 不支持原子的 “升级” 操作,所以只能先解锁再加锁。加上写锁后还要再判定一下是否仍为空树,是的话则建根、解锁、返回,否则应该再 “降级” 为读锁继续后面的操作。
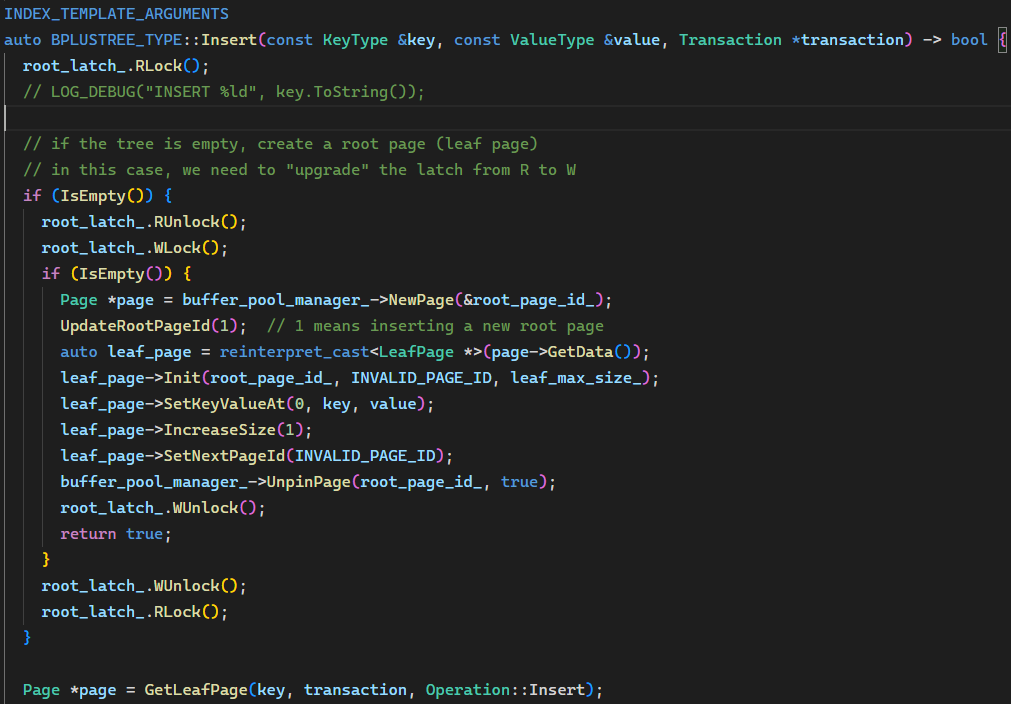
Insert() 结尾部分,现在只需要 Unpin new_tree_page,因为 old_tree_page 都在 ReleaseWLatches() 中处理。
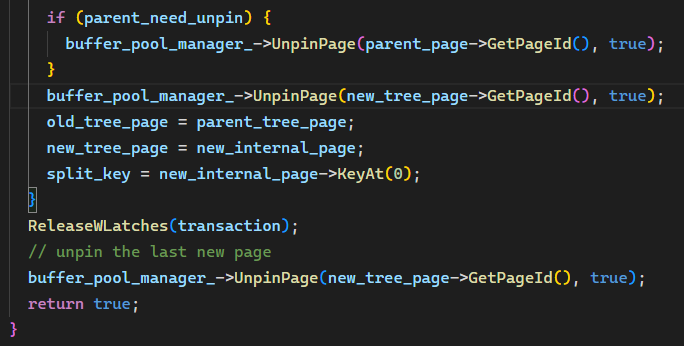
Remove() 本体
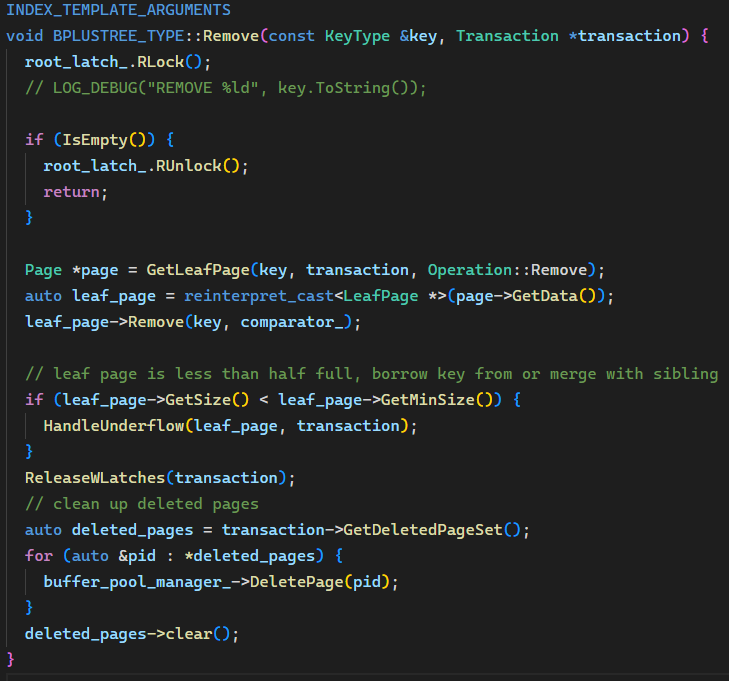
HandleUnderflow() 函数的变化只有:(1)GetPage() 优化 + parent_need_unpin 判断是否要 Unpin;(2)兄弟节点 Fetch 后加写锁以及 ReleaseSiblings 时解锁;(3)MergePage() 后将 right_page 加入 deleted_page_set。逻辑都没有变化,就不重复贴了,可以参考上一篇。
这次优化后的效果还是比较明显的:
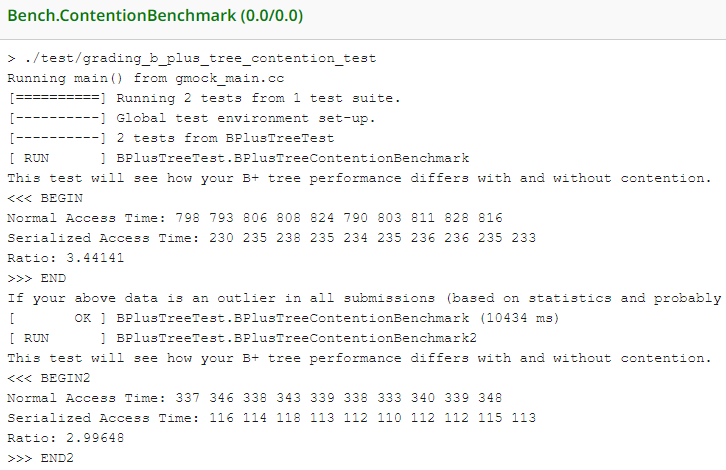
可以看到耗时比已经接近实验讲义给的 3.5 的正常范围上限了,说明并发控制的优化很有效。但 GradeScope 的运行时间并不是很理想,5.51s,大概率是因为本身的实现效率不够高,尤其是 Project 1 Extendible HashTable 和 BufferPoolManager 都是直接一把大锁摆烂实现的,这个结果也比较正常,不想再优化了(逃)
那么本次 Project 2 就到此为止~
2023/03/20 更新:一些小修补
做 Project 3 的时候发现本节的实现有几处小问题:
删除操作中,如果根节点是叶节点且删除后树为空,应将root_page_id_ 重置为 INVALID_PAGE_ID,否则 IsEmpty() 判断空树的结果是错误的。需要修改 HandleUnderflow() 的开始部分: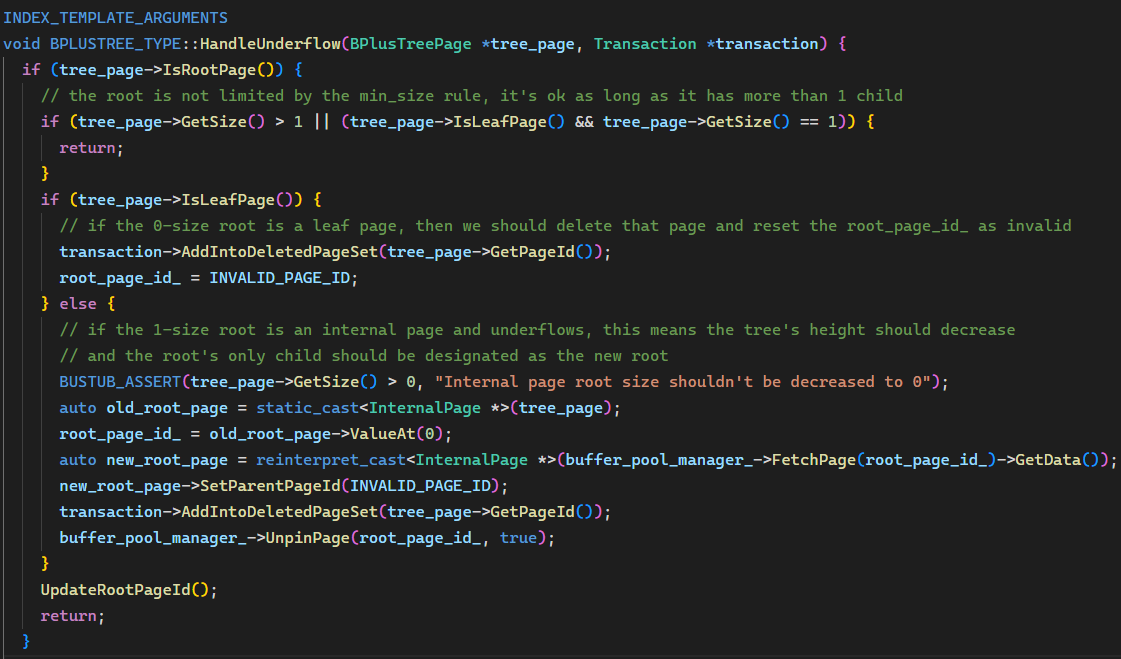 获取
获取 Begin() 迭代器时应先判空,如果是空树直接返回 End()。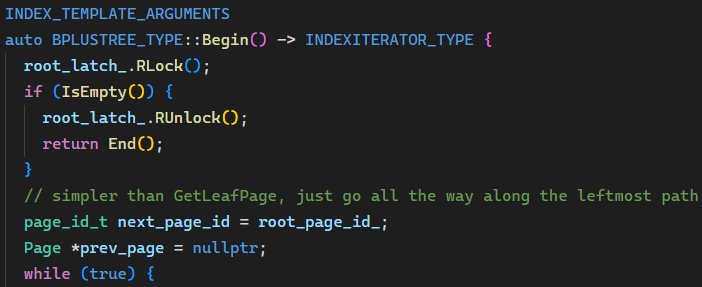
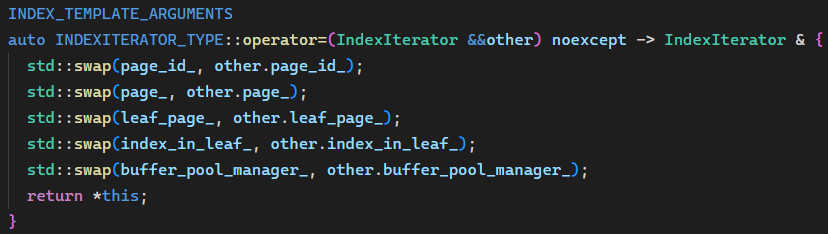
IndexIterator 的实现。之前的设计是 BPlusTree 通过 Begin() 构造 IndexIterator 时对相应 Page 加锁,IndexIterator 析构或跳到下一个页时解锁。这里有一个问题是我们没有关注迭代器的拷贝构造/赋值,如果迭代器被拷贝就会导致同一个 Page 在两个对象的析构中被解锁两次,造成 undefined behavior。实际上这种持有独占性资源的类应该是 move-only 的,所以添加如下代码,仅允许迭代器的移动赋值,移动的实现只要将双方的成员 swap 即可(因为解锁是根据 page_id_ 成员进行的,如果 page_id_ 无效则不会解锁):