文章目录
前言一、单变量线性回归1.导入必要的库2.读取数据3.绘制散点图4.划分数据5.定义模型函数6.定义损失函数7.求权重向量w7.1 梯度下降函数7.2 最小二乘法 8.训练模型9.绘制预测曲线10.试试正则化11.绘制预测曲线12.试试sklearn库 二、多变量线性回归1.导入库2.读取数据3.划分数据4.定义假设函数5.定义损失函数6.定义梯度下降函数7.训练模型8.运用sklearn绘图 总结
前言
线性回归:是一种通过属性的线性组合来进行预测的线性模型
其目的是找到一条直线或者一个平面或者更高维的超平面,使得预测值与真实值之间的误差最小化。
一、单变量线性回归
1.导入必要的库
导入pandas、numpy和matplotlib.pyplot库
import pandas as pd #导入pandas库import numpy as np #导入numpy库import matplotlib.pyplot as plt #导入matplotlib.pyplot库plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签plt.rcParams['axes.unicode_minus']=False #用来正常显示负号2.读取数据
使用pandas库的read_csv()函数读取数据文件,数据文件中包含了人口和收益两列数据
data=pd.read_csv(r"d:线性回归/regress_data1.csv") #读取数据3.绘制散点图
使用data.plot()函数绘制散点图,展示人口与收益之间的关系
data.plot(kind="scatter",x="人口",y="收益") #绘制散点图plt.xlabel("人口",fontsize=10) #横坐标plt.ylabel("收益",fontsize=10) #纵坐标plt.title("人口与收益之间的关系") #标题plt.show() #画图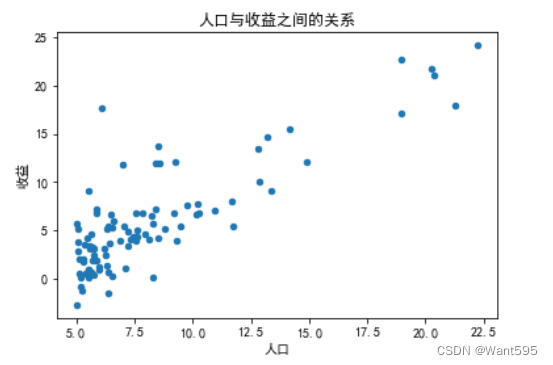
4.划分数据
这里是为了方便后面计算,将一列全为1的列插入到数据中
将数据分为训练集和测试集,这里只使用了训练集
data.insert(0,"ones",1) #插入列,便于后面计算col_num=data.shape[1] #训练特征个数m=data.shape[0] #训练标签个数X=data.iloc[:,:col_num-1].values #训练集的特征y=data.iloc[:,col_num-1].values #训练集的标签y=y.reshape((m,1)) 5.定义模型函数
定义h(X,w)函数用来计算模型预测值,这里采用的是线性模型
def h(X,w): return X@w6.定义损失函数
定义cost(X,y,w)函数用来计算模型误差
def cost(X,y,w): return np.sum(np.power(h(X,w)-y,2))/(2*m)7.求权重向量w
7.1 梯度下降函数
定义函数gradient_descent(X,y,w,n,a)用来执行梯度下降算法,更新权重向量w,并返回最终的权重向量和误差列表
def gradient_descent(X,y,w,n,a): t=w cost_lst=[] for i in range(n): error=h(X,w)-y for j in range(col_num-1): t[j][0]=w[j][0]-((a/m)*np.sum(error.ravel()*X[:,j].ravel())) w=t cost_lst.append(cost(X,y,w)) return w,cost_lst7.2 最小二乘法
定义函数least_square(X,y)用来执行最小二乘法,直接求出权重向量w,但是当n>10000时由于时间复杂度太大将导致程序运行超时
def least_square(X,y): w=np.linalg.inv(X.T@X)@X.T@y return w8.训练模型
调用gradient_descent()函数训练模型,并输出误差随迭代次数变化的图像,用来观察模型的学习效果
其中,迭代次数越大,训练效果越好,学习率适中,既不可太大,也不可过小
n=10000 #迭代次数越多越好a=0.003 #学习率适中,不能太大,也不能太小w=np.zeros((col_num-1,1)) #初始化权重向量w,cost_lst=gradient_descent(X,y,w,n,a) #调用梯度下降函数plt.plot(range(n),cost_lst,"r-+")plt.xlabel("迭代次数")plt.ylabel("误差")plt.show()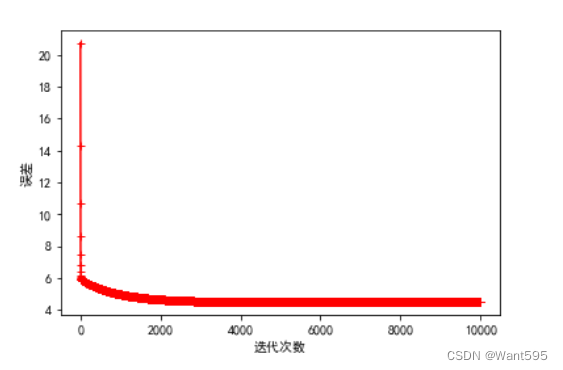
9.绘制预测曲线
使用训练好的权重向量w绘制预测曲线,并将其与原始数据一起绘制在图像上,用来观察模型的预测效果
x=np.linspace(data["人口"].min(),data["人口"].max(),50) #预测特征y1=w[0,0]*1+w[1,0]*x #预测标签plt.scatter(data["人口"],data["收益"], label='训练数据') #训练集plt.plot(x,y1,"r-+",label="预测线") #预测集plt.xlabel("人口",fontsize=10)plt.ylabel("收益",fontsize=10)plt.title("人口与收益之间的关系")plt.show()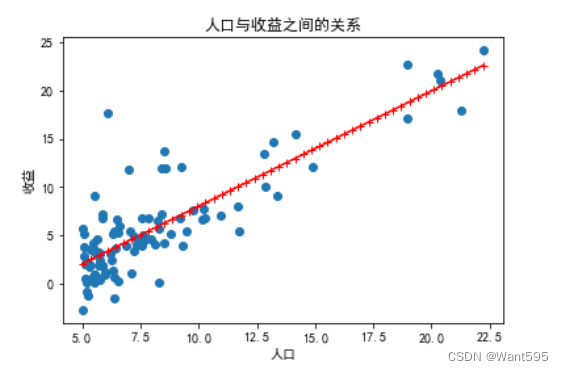
10.试试正则化
使用L2正则化(岭回归)防止过拟合
def gradient_descents(X,y,w,n,a,l): t=w cost_lst=[] for i in range(n): error=h(X,w)-y for j in range(col_num-1): t[j][0]=w[j][0]-((a/m)*(np.sum(error.ravel()*X[:,j].ravel())+2*l*w[j,0])) w=t cost_lst.append(cost(X,y,w)) return w,cost_lstn=10000 #迭代次数越多越好a=0.003 #学习率适中,不能太大,也不能太小l=1 #λw=np.zeros((col_num-1,1))w,cost_lst=gradient_descents(X,y,w,n,a,l)plt.plot(range(n),cost_lst,"r-+")plt.xlabel("迭代次数")plt.ylabel("误差")plt.show()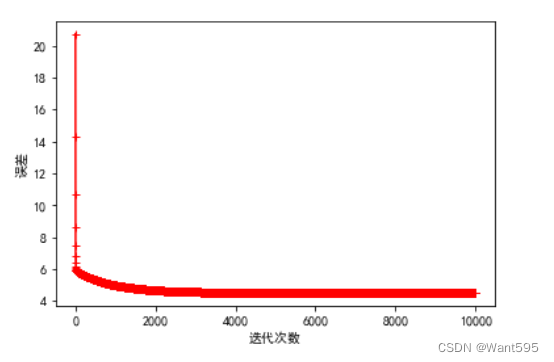
11.绘制预测曲线
使用训练好的权重向量w绘制预测曲线,并将其与原始数据一起绘制在图像上,用来观察模型的预测效果
x=np.linspace(data["人口"].min(),data["人口"].max(),50)y1=w[0,0]*1+w[1,0]*xplt.scatter(data["人口"],data["收益"], label='训练数据')plt.plot(x,y1,"r-+",label="预测线")plt.xlabel("人口",fontsize=10)plt.ylabel("收益",fontsize=10)plt.title("人口与收益之间的关系")plt.show()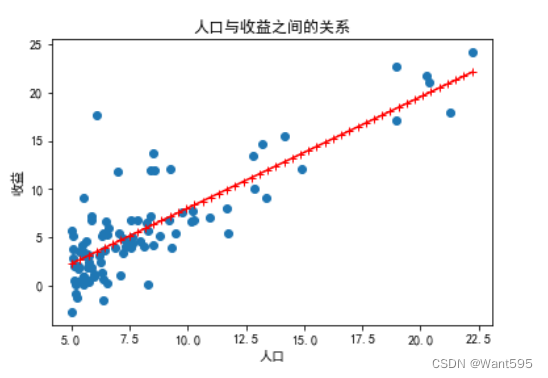
12.试试sklearn库
import pandas as pd #导入pandas库import numpy as np #导入numpy库import matplotlib.pyplot as plt #导入matplotlib.pyplot库 import sklearn #导入sklearn库from sklearn import linear_modelplt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签plt.rcParams['axes.unicode_minus']=False #用来正常显示负号# 2.读取数据:使用pandas库的read_csv()函数读取数据文件。数据文件中包含了人口和收益两列数据。data=pd.read_csv(r"d:线性回归/regress_data1.csv") #读取数据 data.insert(0,"ones",1) #插入列col_num=data.shape[1] #列数m=data.shape[0] #行数# 5.划分数据:将数据分为训练集和测试集,这里只使用了训练集。X=data.iloc[:,:col_num-1].values #训练集的特征y=data.iloc[:,col_num-1].values #训练集的标签y.reshape((m,1))mod=linear_model.LinearRegression()mod.fit(X,y)Y=mod.predict(X)plt.scatter(X[:,1],y,marker='o',color='b')plt.plot(X,Y,marker='+',color='r')plt.xlabel("人口")plt.ylabel("收益")plt.show()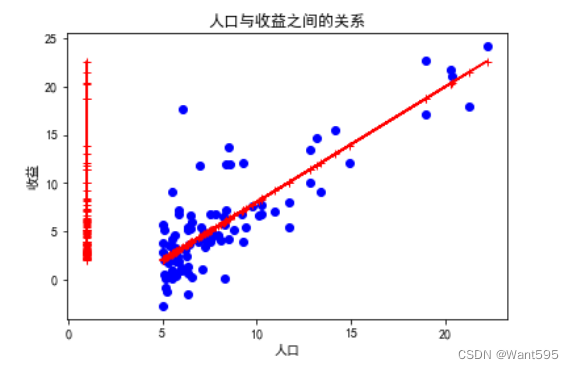
二、多变量线性回归
1.导入库
import pandas as pd #导入pandas库import numpy as np #导入numpy库import matplotlib.pyplot as plt #导入matplotlib.pyplot库plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签plt.rcParams['axes.unicode_minus']=False #用来正常显示负号2.读取数据
datas=pd.read_csv(r"d:/线性回归/regress_data2.csv") #读取数据datas=(datas-datas.mean())/datas.std() #正则化3.划分数据
datas.insert(0,'ones',1) #插入列col_num=datas.shape[1] #训练特征个数m=datas.shape[0] #训练标签X=datas.iloc[:,:col_num-1].values #训练特征y=datas.iloc[:,col_num-1].values #训练标签y=y.reshape((m,1)) 4.定义假设函数
def h(X,w): return X@w5.定义损失函数
def cost(X,y,w): return np.sum(np.power(h(X,w)-y,2))/(2*m)6.定义梯度下降函数
def gradient_descent(X,y,w,n,a): t=w cost_lst=[] for i in range(n): error=h(X,w)-y for j in range(col_num-1): t[j,0]=w[j,0]-((a/m)*np.sum(error.ravel()*X[:,j].ravel())) w=t cost_lst.append(cost(X,y,w)) return w,cost_lst7.训练模型
n=1000 #迭代次数a=0.01 #学习率w=np.zeros((col_num-1,1)) #初始化特征向量ww,cost_lst=gradient_descent(X,y,w,n,a)plt.plot(range(n),cost_lst,'r+-')plt.xlabel("迭代次数")plt.ylabel("误差")plt.show()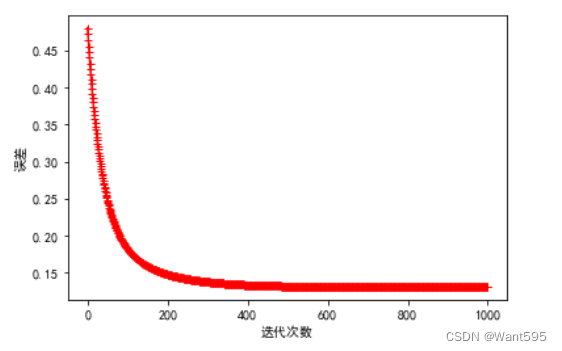
8.运用sklearn绘图
import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn import linear_modelfrom sklearn.preprocessing import PolynomialFeaturesplt.rcParams['font.sans-serif'] = ['SimHei'] plt.rcParams['axes.unicode_minus'] = False # 读取数据datas = pd.read_csv(r"d:线性回归/regress_data2.csv")datas = (datas - datas.mean()) / datas.std()X = datas.iloc[:, :-1].valuesy = datas.iloc[:, -1].values.reshape(-1, 1)# 多项式回归poly = PolynomialFeatures(degree=2)X_poly = poly.fit_transform(X)mod = linear_model.LinearRegression()mod.fit(X_poly, y)# 绘制拟合曲线x1 = np.linspace(datas["面积"].min(), datas["面积"].max(), 50)x2 = np.linspace(datas["房间数"].min(), datas["房间数"].max(), 50)x1, x2 = np.meshgrid(x1, x2)X_grid = np.column_stack((x1.flatten(), x2.flatten()))X_grid_poly = poly.fit_transform(X_grid)y_pred = mod.predict(X_grid_poly)fig=plt.figure()ax = fig.add_subplot(projection='3d')ax.scatter(X[:,0], X[:,1], y, marker='o', color='b')ax.plot_surface(x1, x2, y_pred.reshape(x1.shape), cmap='coolwarm')ax.set_title("价格随面积与房间数的变化曲面")ax.set_xlabel("面积")ax.set_ylabel("房间数")ax.set_zlabel("价格")plt.show()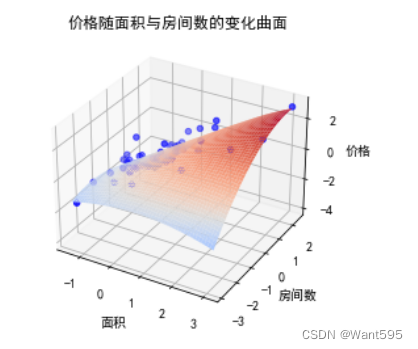
总结
线性回归三大要素
假设函数 h(X,w)损失函数 cost(X,y,w)梯度下降/最小二乘函数(求解权重向量w的函数)普通线性回归步骤
导入库读取数据划分数据假设函数(模型函数)损失函数梯度下降/最小二乘训练模型绘图预测调用sklearn库进行线性回归的步骤
导入库读取数据调用sklearn库绘图