
目录
一.前言
二.二叉树的节点数
二.二叉树的深度
三.二叉树第k层的节点数
四.二叉树的遍历
1.前序遍历
2.中序遍历
3.后序遍历
总结
4.层序遍历
五.二叉树叶节点的个数
一.前言
我们需要先构建个二叉树,方便后续对函数的测试;
还有我们在实现二叉树的这些函数时,尽量少用遍历,这里用的比较多的就是递归和分治思想。
typedef int Tdatatype;typedef struct Tree{Tdatatype data;struct Tree* left;struct Tree* right;}Tree;Tree* BuyTree(Tdatatype x){Tree* node = (Tree*)malloc(sizeof(Tree));if (node == NULL){perror("malloc fail");return NULL;}node->data = x;node->left = NULL;node->right = NULL;return node;}Tree* CreateTree() //这里可以自由操控二叉树的构建{Tree* node1 = BuyTree(1);Tree* node2 = BuyTree(2);Tree* node3 = BuyTree(3);Tree* node4 = BuyTree(4);Tree* node5 = BuyTree(5);Tree* node6 = BuyTree(6);Tree* node7 = BuyTree(7);node1->left = node2;node1->right = node4;node2->left = node3;node2->right = node7;node4->left = node5;node4->right = node6;return node1;}二.二叉树的节点数
二叉树的节点数=左子树的节点数+右子树的节点数;
1.如果root==NULL,则返回0;
2.否则递归调用它的左子树和右子树;
3.然后+1;
详细请看递归调用图:
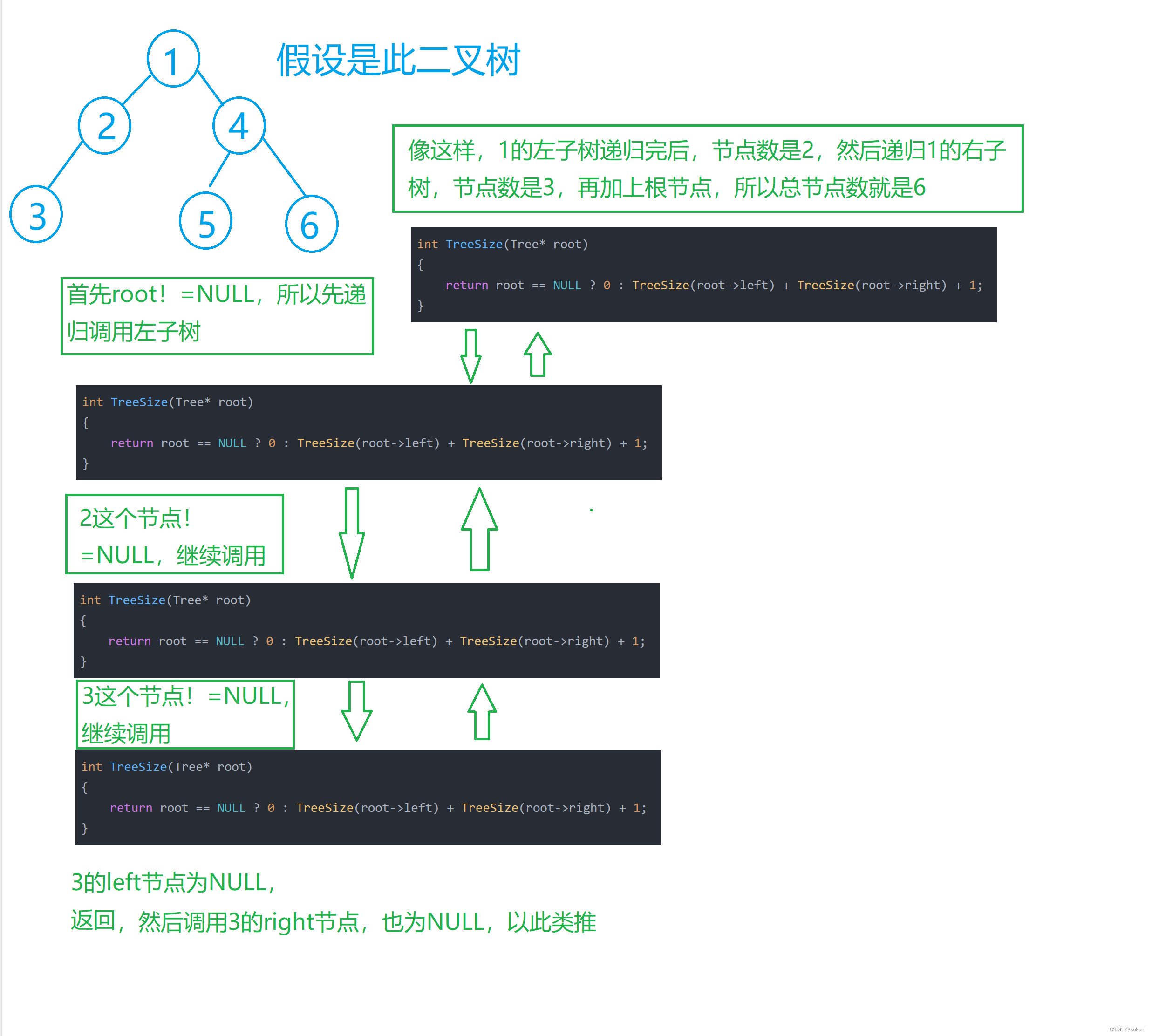
int TreeSize(Tree* root){return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;}二.二叉树的深度
还是利用分治的思想;
1.分别算出左子树和右子树的深度;
2.然后比较二者的大小,大的返回;
3.不要忘了+1,因为根节点也算是一个深度。
int TreeHeight(Tree* root){if (root == NULL) //为空则返回0return 0;int left = TreeHeight(root->left); //要用left记录下其返回值,防止多次重复调用,right同int right = TreeHeight(root->right);return left > right ? left + 1 : right + 1;}三.二叉树第k层的节点数
二叉树第k层的节点数=左子树的第k-1层的节点数+右子树第k-1层的节点数。
因为二叉树没有第0层,是从第一层开始的,所以k==1时,返回1。
int TreeLevel(Tree* root, int k){if (root == NULL) //为空则返回0return 0;if (k == 1)return 1;int left = TreeLevel(root->left, k - 1); //左子树第k-1层节点数int right = TreeLevel(root->right, k - 1); //右子树第k-1层节点数return left + right;}四.二叉树的遍历
1.前序遍历
前序遍历:
1.先访问根节点;
2.然后访问左节点;
3.最后访问右节点;
4.如果节点为空,则结束此次递归调用。
void PreOrder(Tree* root){if (root == NULL)return;printf("%d ", root->data);PreOrder(root->left); //访问左节点PreOrder(root->right); //访问右节点}2.中序遍历
中序遍历:
1.先访问左节点;
2.然后访问根节点;
3.最后访问右节点;
4.如果节点为空,则结束此次递归调用。
void InOrder(Tree* root){if (root == NULL)return;InOrder(root->left);printf("%d ", root->data);InOrder(root->right);}3.后序遍历
后序遍历:
1.先访问左节点;
2.然后访问右节点;
3.最后访问根节点;
4.如果节点为空,则结束此次递归调用。
void PostOrder(Tree* root){if (root == NULL)return;PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);}总结
通过以上代码我们发现:
1.假设前序,中序,后序分别为1,2,3;
2.是哪个序遍历,就按照那个顺序访问根节点,左节点永远在右节点前面;
3.递归也是按照这个顺序。
4.层序遍历
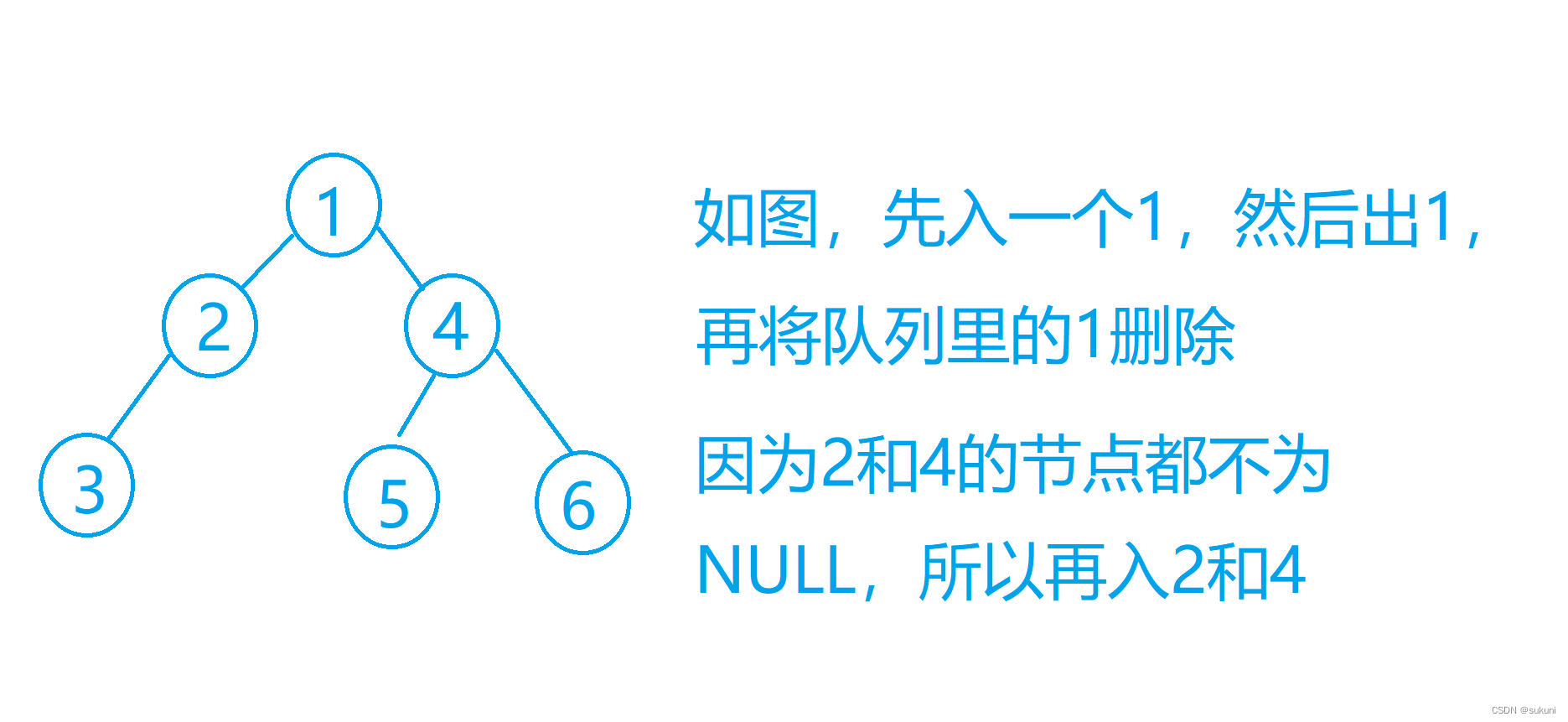
层序遍历就需要用到队列了。
1.先入一个节点进队列,此时队列不为空;
2。然后出一个节点,然后删除队列里的一个元素,如果左节点和右节点不为空的话,入它的左节点和右节点;
3.队列为空时跳出循环。
void LevelOrder(Tree* root){ //创建一个队列,并初始化Queue q;Queueinit(&q);if (root)Queuepush(&q, root);while (!Queueempty(&q)){Tree* front = Queuefront(&q); //出一个数据Queuepop(&q);printf("%d ", front->data);if (front->left)Queuepush(&q,front->left); //入它的左节点if (front->right)Queuepush(&q, front->right); //入它的右节点}Queuedestroy(&q); //不要忘记销毁队列}五.二叉树叶节点的个数
叶节点就是没有子节点的节点,我们可以分别记录下当前节点的左节点和右节点,如果都为空,那么叶节点的个数+1。
int BinaryTreeLeafSize(Tree* root){Tree* left = root->left;Tree* right = root->right;if (left == NULL && right == NULL){return 1;}else{BinaryTreeLeafSize(root->left);BinaryTreeLeafSize(root->right);}}??本篇文章到此就结束了,若有错误或是建议的话,欢迎小伙伴们指出;?️?
??希望小伙伴们能支持支持博主啊,你们的支持对我很重要哦;??
??谢谢你的阅读。??
