遗传算法之路径规划matlab代码（栅格地图）含详细注释

遗传算法本人在另一篇博文中已经有记载，本次将遗传算法用于路径规划的代码记录于此，用于大家一起学习 一起进步，如果有用，欢迎点赞。

1.基于遗传算法的栅格法机器人路径规划main.m

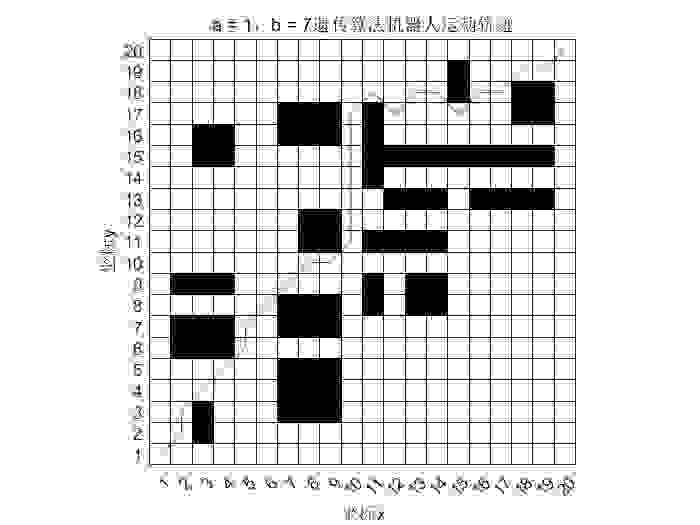
% 基于遗传算法的栅格法机器人路径规划%jubobolv369clc;clear;% 输入数据,即栅格地图.20行20列Grid=  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;     0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;     0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;     0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;     0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;     0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;     0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;     0 0 0 0 0 0 1 1 1 0 1 0 1 1 0 0 0 0 0 0;     0 1 1 1 0 0 0 0 0 0 1 0 1 1 0 0 0 0 0 0;     0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;     0 0 0 0 0 0 0 1 1 0 1 1 1 1 0 0 0 0 0 0;     0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0;     0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 1 1 1 1 0;     0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0;     0 0 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0;     0 0 1 1 0 0 1 1 1 0 1 0 0 0 0 0 0 0 0 0;     0 0 0 0 0 0 1 1 1 0 1 0 0 0 0 0 0 1 1 0;      0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0;     0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0;     0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]; start_num = 0;    % 起点编号end_num = 399;    % 终点序号NP = 200;       % 种群数量max_gen = 50;  % 最大进化代数pc = 0.8;      % 交叉概率pm = 0.2;      % 变异概率a = 1;         % 路径长度比重b = 7;         % 路径顺滑度比重z = 1;         new_pop1 = {}; % 元胞数组，存放路径[y, x] = size(Grid);% 起点所在列（从左到右编号1.2.3...）start_column = mod(start_num, x) + 1; % 起点所在行（从上到下编号行1.2.3...）start_row = fix(start_num / x) + 1;  %Y = fix(X) 将 X 的每个元素朝零方向四舍五入为最近的整数% 终点所在列、行end_column = mod(end_num, x) + 1;end_row = fix(end_num / x) + 1; %% 种群初始化step1，必经节点,从起始点所在行开始往上，在每行中挑选一个自由栅格，构成必经节点pass_num = end_row - start_row + 1;  %每条路径的节点个数pop = zeros(NP, pass_num);%生成种群数量*节点个数的矩阵，用于存放每个个体的路径for i = 1 : NP  %每个个体（每行）循环操作：    pop(i, 1) = start_num;   %每行第一列都为起点(存入起点的编号)    j = 1;    % 此for循环用于寻找除去起点和终点所在行以外每行中的自由栅格    for row_i = start_row+1 : end_row-1   %栅格的第二行到倒数第二行循环        j = j + 1;        % 存放栅格里当前行中的自由栅格序号        free = [];         for column_i = 1 : x   %从第一列到第二十列中            % 栅格对应的序号            num = (column_i - 1) + (row_i - 1) * x;% 如果该栅格为非障碍物            if Grid(row_i, column_i) == 0                % 把此栅格的编号加入free矩阵中                free = [free num];            end        end     % 栅格一行里的自由栅格查询结束，自由栅格的编号存在了向量中        free_num = length(free);        % 产生小于等于本行自由栅格数量的一个随机整数        index = randi(free_num); %X = randi(imax) 返回一个介于 1 和 imax 之间的伪随机整数标量。        % 将栅格中当前行的自由栅格矩阵free中第index个栅格编号作为当前种群的第j个节点        pop(i, j) = free(index);      end  %该个体的每一行的路径节点产生完成,存入了pop的第i行中    pop(i, end) = end_num; %pop的每行第最后一列都为终点(存入终点的编号)    %% 种群初始化step2将上述必经节点联结成无间断路径    single_new_pop = generate_continuous_path(pop(i, :), Grid, x);      if ~isempty(single_new_pop)%如果这一行种群的路径不是空的，将这行路径存入元胞数组中。       new_pop1(z, 1) = {single_new_pop};        z = z + 1;    endend %% 计算初始化种群的适应度% 计算路径长度path_value = cal_path_value(new_pop1, x);% 计算路径平滑度path_smooth = cal_path_smooth(new_pop1, x);fit_value = a .* path_value .^ -1 + b .* path_smooth .^ -1; mean_path_value = zeros(1, max_gen);min_path_value = zeros(1, max_gen);%% 循环迭代操作for i = 1 : max_gen    % 选择操作    new_pop2 = selection(new_pop1, fit_value);    % 交叉操作    new_pop2 = crossover(new_pop2, pc);    % 变异操作    new_pop2 = mutation(new_pop2, pm, Grid, x);    % 更新种群    new_pop1 = new_pop2;    % 计算适应度值    % 计算路径长度    path_value = cal_path_value(new_pop1, x)    % 计算路径平滑度    path_smooth = cal_path_smooth(new_pop1, x)    fit_value = a .* path_value .^ -1 + b .* path_smooth .^ -1    mean_path_value(1, i) = mean(path_value);    [~, m] = max(fit_value);    min_path_value(1, i) = path_value(1, m);end%% 画每次迭代平均路径长度和最优路径长度图figure(1)plot(1:max_gen,  mean_path_value, 'r')hold on;title(['a = ', num2str(a)', '，b = ',num2str(b)','的优化曲线图']); xlabel('迭代次数'); ylabel('路径长度');plot(1:max_gen, min_path_value, 'b')legend('平均路径长度', '最优路径长度');min_path_value(1, end)% 在地图上画路径[~, min_index] = max(fit_value);min_path = new_pop1{min_index, 1};figure(2)hold on;title(['a = ', num2str(a)', '，b = ',num2str(b)','遗传算法机器人运动轨迹']); xlabel('坐标x'); ylabel('坐标y');DrawMap(Grid);[~, min_path_num] = size(min_path);for i = 1:min_path_num    % 路径点所在列（从左到右编号1.2.3...）    x_min_path(1, i) = mod(min_path(1, i), x) + 1;     % 路径点所在行（从上到下编号行1.2.3...）    y_min_path(1, i) = fix(min_path(1, i) / x) + 1;endhold on;plot(x_min_path, y_min_path, 'r')

2.将必经节点联结成无间断路径，如果结点间不连续，则插入节点使其连续generate_continuous_path.m

% 将必经节点联结成无间断路径，如果结点间不连续，则插入节点使其连续。%jubobolv369function [single_new_pop] = generate_continuous_path(single_pop, Grid, x)i = 1;single_new_pop = single_pop;  %传入的某行的初始路径，有20个路径节点[~, single_path_num] = size(single_new_pop);%遍历该行的所有节点，使其连续while i ~= single_path_num%%定位第i、i+1个节点的坐标    % 路径中第i个栅格在地图的列（从左到右编号1.2.3...）    column_now = mod(single_new_pop(1, i), x) + 1;     % 路径中第i个栅格在地图的行（从上到下编号行1.2.3...）    row_now = fix(single_new_pop(1, i) / x) + 1;    % 路径中第i+1个栅格在地图的列、行    column_next = mod(single_new_pop(1, i + 1), x) + 1;    row_next = fix(single_new_pop(1, i + 1) / x) + 1;        % 初始化最大迭代次数    max_iteration = 0;        %% 判断点i和i+1是否连续,若不连续插入值(如果前后两节点的X坐标与Y坐标的差中较大值不等于1，说明不连续)while max(abs(column_next - column_now), abs(row_next - row_now)) ~= 1%取两节点的中点作为插入点,见forGA_word.xls-sheet1%插入点的横坐标 x_insert，纵坐标 y_insert        x_insert = floor((column_next + column_now) / 2);%Y = floor(X) 将 X 的每个元素四舍五入到小于或等于该元素的最接近整数。        y_insert = floor((row_next + row_now) / 2);                % 插入栅格为自由栅格        if Grid(y_insert, x_insert) == 0              % 插入的栅格序号            num_insert = (x_insert - 1) + (y_insert - 1) * x;            % 插入新序号（将当前的栅格序号中间插入一个新栅格序号 其他保持不变）            single_new_pop = [single_new_pop(1, 1:i), num_insert, single_new_pop(1, i+1:end)];                    % 插入栅格为障碍物栅格        else               % 往左走(如果当前待插入格（障碍物格)的左邻格不是障碍物 且 左邻格不是当前研究的两个格中任意一个)            if Grid(y_insert, x_insert - 1) == 0 && ((x_insert - 2) + (y_insert - 1) * x ~= single_new_pop(1, i)) && ((x_insert - 2) + (y_insert - 1) * x ~= single_new_pop(1, i+1))                x_insert = x_insert - 1;                % 栅格序号                num_insert = (x_insert - 1) + (y_insert - 1) * x;                % 插入新序号                single_new_pop = [single_new_pop(1, 1:i), num_insert, single_new_pop(1, i+1:end)];                                           % 往右走 (如果当前待插入格（障碍物格)的右邻格不是障碍物 且 右邻格不是当前研究的两个格中任意一个)               elseif Grid(y_insert, x_insert + 1) == 0 && (x_insert + (y_insert - 1) * x ~= single_new_pop(1, i)) && (x_insert + (y_insert - 1) * x ~= single_new_pop(1, i+1))                x_insert = x_insert + 1;                % 栅格序号                num_insert = (x_insert - 1) + (y_insert - 1) * x;                % 插入新序号                single_new_pop = [single_new_pop(1, 1:i), num_insert, single_new_pop(1, i+1:end)];                            % 向上走            elseif Grid(y_insert + 1, x_insert) == 0 && ((x_insert - 1) + y_insert * x ~= single_new_pop(1, i)) && ((x_insert - 1) + y_insert * x ~= single_new_pop(1, i+1))                y_insert = y_insert + 1;                % 栅格序号                num_insert = (x_insert - 1) + (y_insert - 1) * x;                % 插入新序号                single_new_pop = [single_new_pop(1, 1:i), num_insert, single_new_pop(1, i+1:end)];             % 向下走            elseif  Grid(y_insert - 1, x_insert) == 0 && ((x_insert - 1) + (y_insert - 2) * x ~= single_new_pop(1, i)) && ((x_insert - 1) + (y_insert-2) * x ~= single_new_pop(1, i+1))                y_insert = y_insert - 1;                % 栅格序号                num_insert = (x_insert - 1) + (y_insert - 1) * x;                % 插入新序号                single_new_pop = [single_new_pop(1, 1:i), num_insert, single_new_pop(1, i+1:end)];                            % 如果各方向都无法插入则舍去此路径            else                %break_pop = single_new_pop                single_new_pop = [];                break            end            end                column_next = x_insert;        row_next = y_insert;        max_iteration = max_iteration + 1;%如果可以不断的增加新节点，但增加次数超过20000次，则舍弃此路径        if max_iteration > 20000            single_new_pop = [];            break        end            end        if isempty(single_new_pop)        break    end        [~, single_path_num] = size(single_new_pop);    i = i + 1;end

3.计算路径长度函数cal_path_value.m

%% 计算路径长度函数%jubobolv369function [path_value] = cal_path_value(pop, x)[n, ~] = size(pop);path_value = zeros(1, n);%循环计算每一条路径的长度for i = 1 : n    single_pop = pop{i, 1};    [~, m] = size(single_pop);    %路径有m个栅格，需要计算m-1次    for j = 1 : m - 1        % 点i所在列（从左到右编号1.2.3...）        x_now = mod(single_pop(1, j), x) + 1;         % 点i所在行（从上到下编号行1.2.3...）        y_now = fix(single_pop(1, j) / x) + 1;        % 点i+1所在列、行        x_next = mod(single_pop(1, j + 1), x) + 1;        y_next = fix(single_pop(1, j + 1) / x) + 1;        %如果相邻两个栅格为上下或左右，路径长度加1，否则为对角线，长度加根号2        if abs(x_now - x_next) + abs(y_now - y_next) == 1            path_value(1, i) = path_value(1, i) + 1;        else            path_value(1, i) = path_value(1, i) + sqrt(2);        end    endend

4.计算路径平滑度函数cal_path_smooth.m

%% 计算路径平滑度函数%jubobolv369function [path_smooth] = cal_path_smooth(pop, x)[n, ~] = size(pop);path_smooth = zeros(1, n);%循环计算每一条路径的平滑度for i = 1 : n    single_pop = pop{i, 1};    [~, m] = size(single_pop);    %路径有m个栅格，需要计算m-1次    for j = 1 : m - 2        % 点i所在列（从左到右编号1.2.3...）        x_now = mod(single_pop(1, j), x) + 1;         % 点i所在行（从上到下编号行1.2.3...）        y_now = fix(single_pop(1, j) / x) + 1;        % 点i+1所在列、行        x_next1 = mod(single_pop(1, j + 1), x) + 1;        y_next1 = fix(single_pop(1, j + 1) / x) + 1;        % 点i+2所在列、行        x_next2 = mod(single_pop(1, j + 2), x) + 1;        y_next2 = fix(single_pop(1, j + 2) / x) + 1;        %path_smooth(1, i) = path_smooth(1, i) + abs(atan(abs(x_now - x_next1)/abs(y_now - y_next1))-atan(abs(x_next2 - x_next1)/abs(y_next2 - y_next1)));        %a2 = (x_now - x_next1)^2 + (y_now - y_next1)^2;        %b2 = (x_next2 - x_next1)^2 + (y_next2 - y_next1)^2;        c2 = (x_now - x_next2)^2 + (y_now - y_next2)^2;        %angle = (a2 + c2 - b2) / (2 * sqrt(a2) *  sqrt(c2));        %若大于4小于等于8，说明此栅格与隔一个的栅格隔一行或一列且列或行相邻        if c2 < 8 && c2 > 4            path_smooth(1, i) = path_smooth(1, i) + 5;        %若大于1小于等于4，说明此栅格与隔一个的栅格为对角，也可能或同行或同列垮了一格        elseif c2 <= 4 && c2 > 1            path_smooth(1, i) = path_smooth(1, i) + 30;        %若等于1，说明此栅格与隔一个的栅格是上下或左右相邻，其路径不如直接从此格到邻格，显然冗余了。        elseif    c2 <= 1            path_smooth(1, i) = path_smooth(1, i) + 5000;        %否则不设置值，也即值为0，此时此栅格与隔一个的栅格是正方形对角的关系，最好。        end    endend

5.用轮盘堵法选择新的个体selection.m

%% 用轮盘堵法选择新的个体% 输入变量：pop元胞种群，fitvalue：适应度值% 输出变量：newpop选择以后的元胞种群%jubobolv369function [new_pop] = selection(pop, fit_value)%构造轮盘[px, ~] = size(pop);total_fit = sum(fit_value);p_fit_value = fit_value / total_fit;p_fit_value = cumsum(p_fit_value);    % B = cumsum(A) 从 A 中的第一个其大小不等于 1 的数组维度开始返回 A 的累积和。% 随机数从小到大排列ms = sort(rand(px, 1));   fitin = 1;newin = 1;while newin <= px    if(ms(newin)) < p_fit_value(fitin)        new_pop{newin, 1} = pop{fitin, 1};        newin = newin+1;    else        fitin = fitin+1;    endend

6.交叉操作crossover.m

%%交叉操作%输入变量：pop：父代种群，pc：交叉的概率%输出变量：newpop：交叉后的种群%jubobolv369function [new_pop] = crossover(pop, pc)[px,~] = size(pop);% 判断路径点数是奇数或偶数parity = mod(px, 2);new_pop = {};%两个两个交叉for i = 1:2:px-1        singal_now_pop = pop{i, 1};        singal_next_pop = pop{i+1, 1};        %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%       %%         A = [5 3 4 2];                %%       %%         B = [2 4 4 4 6 8];            %%       %%        [Lia,Locb] = ismember(A,B)     %%       %%         Lia = 1x4 logical array       %%A的每个元素若B中存在则该位为1 否则为零       %%                 0   0   1   1         %%       %%         Locb = 1×4                   %%每个相同的元素在B中的索引       %%                 0     0     2     1   %%        %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%        [lia, locb] = ismember(singal_now_pop, singal_next_pop);%[Lia,Locb] = ismember(A,B)确定 A 的哪些元素同时也在 B 中及其在 B 中的相应位置。        [~, n] = find(lia == 1);%要查找特定的整数值，使用 == 运算符。返回找到的值在lia中的索引        [~, m] = size(n);        %如果随机数小于交叉概率且A中有三个以上路径节点与B中的相同    if (rand < pc) && (m >= 3)        % 生成一个2到m-1之间的随机数，也就是除去开头和结尾，在两条路径的相同节点中随机选取一个节点用于交叉        r = round(rand(1,1)*(m-3)) +2;%Y = round(X) 将 X 的每个元素四舍五入为最近的整数        crossover_index1 = n(1, r);%        crossover_index2 = locb(crossover_index1);        new_pop{i, 1} = [singal_now_pop(1:crossover_index1), singal_next_pop(crossover_index2+1:end)];        new_pop{i+1, 1} = [singal_next_pop(1:crossover_index2), singal_now_pop(crossover_index1+1:end)];            else   %否则不交叉        new_pop{i, 1} =singal_now_pop;        new_pop{i+1, 1} = singal_next_pop;    end    %如果有奇数条路径，除最后一条外，其余已按照if的条件进行了是否交叉的处理，所以最后一条仍然不变。if parity == 1    new_pop{px, 1} = pop{px, 1};endend

7.变异操作mutation.m

%% 变异操作% 函数说明% 输入变量：pop：种群，pm：变异概率% 输出变量：newpop变异以后的种群%jubobolv369function [new_pop] = mutation(pop, pm, Grid, x)[px, ~] = size(pop);new_pop = {};%对每一行选择是否变异for i = 1:px    % 初始化最大迭代次数    max_iteration = 0;    single_new_pop = pop{i, 1};    [~, m] = size(single_new_pop);    % single_new_pop_slice初始化    single_new_pop_slice = [];    if(rand < pm)        while isempty(single_new_pop_slice)            % 生成2到（m-1）的两个随机数,并排序            mpoint = sort(round(rand(1,2)*(m-3)) + [2 2]);            %切除掉包含两个随机数在内的之间的路径节点，将切除部分及前后两个节点取出            single_new_pop_slice = [single_new_pop(mpoint(1, 1)-1) single_new_pop(mpoint(1, 2)+1)];            %将取出的用于切除的部分路径重新联结成无间断路径(这一步可能变异 也可能不变异)            single_new_pop_slice = generate_continuous_path(single_new_pop_slice, Grid, x);            %max_iteration = max_iteration + 1;            if max_iteration >= 100000                break            end        end        if max_iteration >= 100000            new_pop{i, 1} = pop{i, 1};        else            %将变异后的路径保存            new_pop{i, 1} = [single_new_pop(1, 1:mpoint(1, 1)-1), single_new_pop_slice(2:end-1), single_new_pop(1, mpoint(1, 2)+1:m)];        end        % single_new_pop_slice再次初始化        single_new_pop_slice = [];    else%不变异        new_pop{i, 1} = pop{i, 1};    endend

8.创建具有障碍物的栅格地图DrawMap.m

%创建具有障碍物的栅格地图%矩阵中1代表黑色栅格%jubobolv369function Grid = DrawMap(Grid)b = Grid;b(end+1,end+1) = 0;colormap([1 1 1;0 0 0]);  % 创建颜色pcolor(0.5:size(Grid,2) + 0.5, 0.5:size(Grid,1) + 0.5, b); % 赋予栅格颜色set(gca, 'XTick', 1:size(Grid,1), 'YTick', 1:size(Grid,2));  % 设置坐标axis image xy;  % 沿每个坐标轴使用相同的数据单位，保持一致

如果急看，可至此处，压缩包包含代码和本人学习时候的草稿。喜欢请点赞哦。

链接: https://pan.baidu.com/s/19Z0huAtdR5x2WmBQdAbhHg

提取码: uzdu