目录
ADF检验简介adftest的使用及参数介绍——简单调用:h = adftest(y)——多参数调用:[h,pValue,stat,cValue] = adftest(y,'alpha',0.05) adftest如何判断是否平稳?——原假设与备择假设——通过h判断是否平稳——通过pValue判单是否平稳——通过stat和cValue判断是否平稳 应用举例(以1978年到2020年的中国GDP为例):原始序列的ADF检验一阶差分序列的ADF检验二阶差分序列 完整代码及数据作者水平有限,第一次发文,有错误及需要改正的地方请指正
ADF检验简介
ADF检验全称为Augmented Dickey-Fuller test。通常在使用时间序列模型(如ARMA,ARIMA)的时候用于检验时间序列数据的平稳性。他主要通过检验数据是否有单位根判断序列是否平稳。
adftest的使用及参数介绍
——简单调用:h = adftest(y)
输入参数:
y:进行检验的时间序列
输出参数:
h:检验结果
h = 0,说明序列不平稳;
h = 1,说明序列平稳。
——多参数调用:[h,pValue,stat,cValue] = adftest(y,‘alpha’,0.05)
输入参数:
y:进行检验的时间序列
‘alpha’,0.05:组合起来使用可以改变假设检验的显著性水平,如果不设置则默认为0.05
输出参数:
h:检验结果
pValue:假设检验的P值,依据他的大小可以判断是否拒绝原假设
stat:检验统计量,与cValue一起可以决定是否拒绝原假设
cValue:假设检验的临界值,与stat一起可以决定是否拒绝原假设
(下文会介绍三种利用输出参数判断是否平稳的方法,他们的结果是统一的,会一种就行)
adftest如何判断是否平稳?
——原假设与备择假设
原假设:存在单位根(时间序列不平稳)
备择假设:不存在单位根(时间序列平稳)
——通过h判断是否平稳
h = 0时,我们无法拒绝原假设,也就是接受原假设→序列存在单位根→时间序列不平稳
h = 1时,我们拒绝原假设→序列不存在单位根→时间序列平稳
——通过pValue判单是否平稳
pValue>0.05(显著性水平,这里用0.05举例):我们无法拒绝原假设,也就是接受原假设→序列存在单位根→时间序列不平稳
pValue<0.05:我们拒绝原假设→序列不存在单位根→时间序列平稳
——通过stat和cValue判断是否平稳
stat>cValue:落在接受域,我们无法拒绝原假设,也就是接受原假设→序列存在单位根→时间序列不平稳
stat<cValue:落在拒绝域,我们拒绝原假设→序列不存在单位根→时间序列平稳
应用举例(以1978年到2020年的中国GDP为例):
原始序列的ADF检验
clc;clear;data = readtable("data.xlsx");data = table2array(data);data = data(:,2)plot(data,'LineWidth',1.5)[h,pValue,stat,cValue] = adftest(data,'alpha',0.05)输出结果为:
h = 0; (h等于0→接受原假设→有单位根→不平稳)
pValue = 0.9990 (p大于0.05→接受原假设→有单位根→不平稳)
stat = 13.4332 (stat>cValue→接受原假设→有单位根→不平稳)
cValue = -1.9474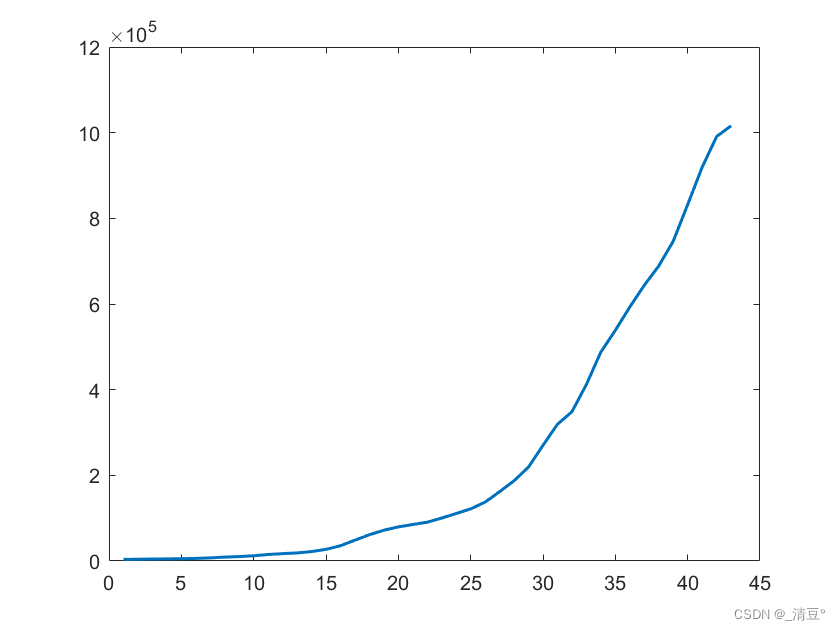
从折线图和函数返回结果看,该序列都是不平稳的。
一阶差分序列的ADF检验
%% 接上述代码datad1 = diff(data,1)figureplot(datad1,'LineWidth',1.5)[h,pValue,stat,cValue] = adftest(datad1,'alpha',0.05)输出结果为:
h = 0;
pValue = 0.2810
stat = -0.9989
cValue = -1.9475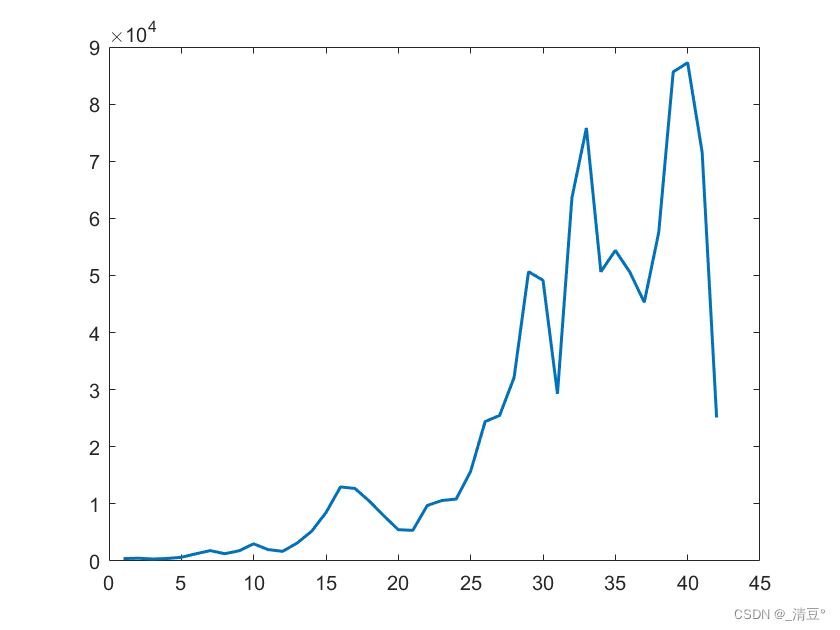
从折线图可见一阶差分仍然具有显著上升趋势,序列不平稳,与函数返回结果契合。
二阶差分序列
datad2 = diff(data,2)figureplot(datad2,'LineWidth',1.5)[h,pValue,stat,cValue] = adftest(datad2,'alpha',0.05)输出结果为:
h = 1;
pValue = 1.0000e-03
stat = -4.3792
cValue = -1.9476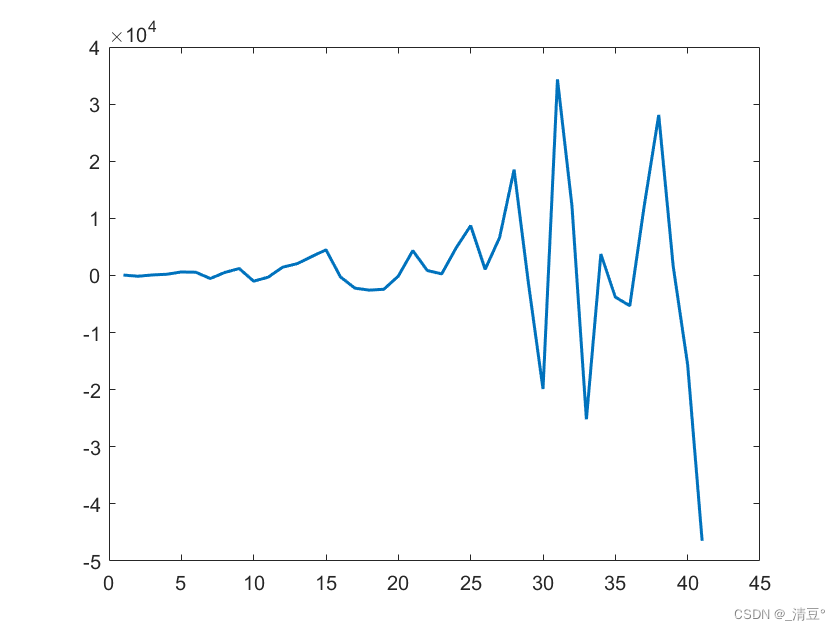
由折线图,数据在0附近随机波动,表现为平稳序列,与函数返回值契合。
完整代码及数据
clc;clear;data = readtable("data.xlsx");data = table2array(data);data = data(:,2)%可注释上面三行,将下一行取消注释%data = [3678.702500000004100.453700000004587.581100000004935.832800000005373.350100000006020.924100000007278.502300000009098.9480000000010376.154500000012174.594700000015180.386500000017179.741700000018872.868800000022005.628500000027194.530900000035673.230400000048637.450300000061339.891300000071813.629600000079715.044500000085195.507100000090564.3758000000100280.139300000110863.123000000121717.424700000137422.034900000161840.160900000187318.903100000219438.474800000270092.323700000319244.612800000348517.743700000412119.255800000487940.180500000538579.953500000592963.229500000643563.104500000688858.218000000746395.059500000832035.948600000919281.129100000990865.1113000001015986.20000000]'plot(data,'LineWidth',1.5)[h,pValue,stat,cValue] = adftest(data,'alpha',0.05)%% 一阶差分datad1 = diff(data,1)figureplot(datad1,'LineWidth',1.5)[h,pValue,stat,cValue] = adftest(datad1,'alpha',0.05)%% 二阶差分datad2 = diff(data,2)figureplot(datad2,'LineWidth',1.5)[h,pValue,stat,cValue] = adftest(datad2,'alpha',0.05)%adftest:原假设:存在单位根(说明这是一个非平稳的时间序列) 备择假设:不存在单位根(说明这是一个平稳时间序列)%h = 0则不能拒绝原假设,那么接受原假设,说明时间序列不平稳