转速、电流双闭环控制的引出
转速单闭环控制直流调速系统用PI调节器实现转速稳态无静差,消除负载转矩扰动对稳态转速的影响,并用电流截止负反馈限制电枢电流的冲击,避免出现过流现象。但转速单闭环系统并不能按照要求充分控制电流的动态过程。
转速环控制的理想状态
在电机起动过程中只有电力负反馈,没有转速负反馈,在到达稳态转速后,又希望转速负反馈发挥主要作用,使转速跟随给定,而电流负反馈不要起阻碍作用。为了使转速和电流两种负反馈分别起作用,可在系统中设置两个调节器,分别引入转速负反馈和电流负反馈以调节转速和电流,二者之间实行嵌套。从闭环结构上看,电流环在里面,称作内环;转速环在外边,称作外环。这就形成了转速、电流双闭环控制直流调速系统。
4.1 双闭环调速系统的组成和静特性分析
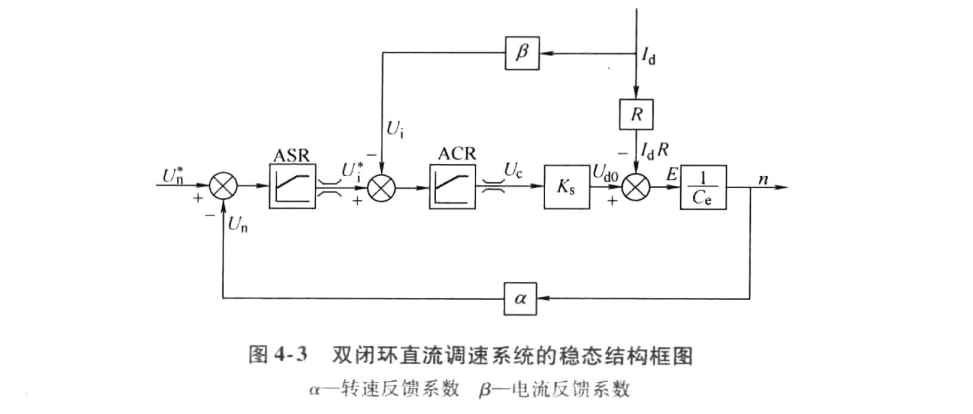
双闭环调速系统工作在稳态中,当两个调节器都不饱和时,各变量之间有下列关系
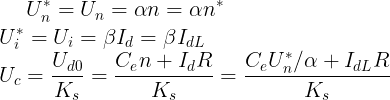
在稳态工作点上,转速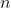 是由给定电压
是由给定电压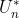 决定的,ASR的输出量
决定的,ASR的输出量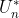 是由负载电流
是由负载电流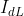 决定的,而ACR的输出量控制电压
决定的,而ACR的输出量控制电压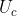 的大小则同时取决于
的大小则同时取决于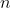 和
和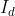
P控制器和PI控制器的区别
P控制器的输出量总是正比于其输入量的。而PI控制器的饱和输出为限幅值,而非饱和输出在动态过程中取决于输入量的积分。到达稳态时,输入为零,输出的稳态值是由它后面环节的需要决定的,后面需要PI控制器提供多达的输出值,它都能做到,直到饱和为止。
双闭环调速系统的静特性
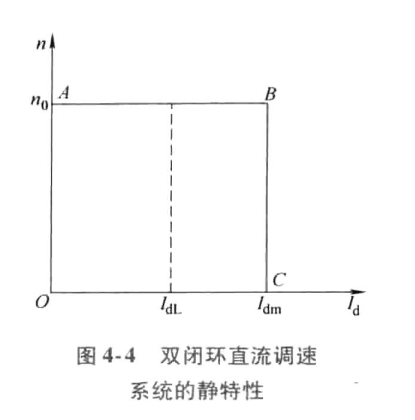
双闭环调速系统的静特性在负载电流小于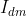 时表现为转速无静差,这时,转速负反馈起主要调节作用。当负载电流达到
时表现为转速无静差,这时,转速负反馈起主要调节作用。当负载电流达到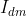 时,对应于转速调节器为饱和输出
时,对应于转速调节器为饱和输出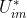 ,这时电流调节器起主要调节作用,系统表现为电流无静差,起到过电流的自动保护作用,电机在一段时间内以最大电枢电流加速或减速。
,这时电流调节器起主要调节作用,系统表现为电流无静差,起到过电流的自动保护作用,电机在一段时间内以最大电枢电流加速或减速。
4.2 双闭环调速系统的动态过程分析
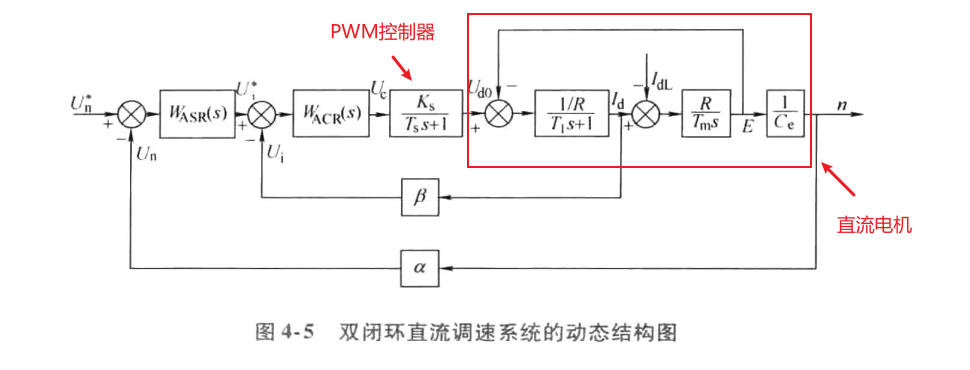
起动过程分析
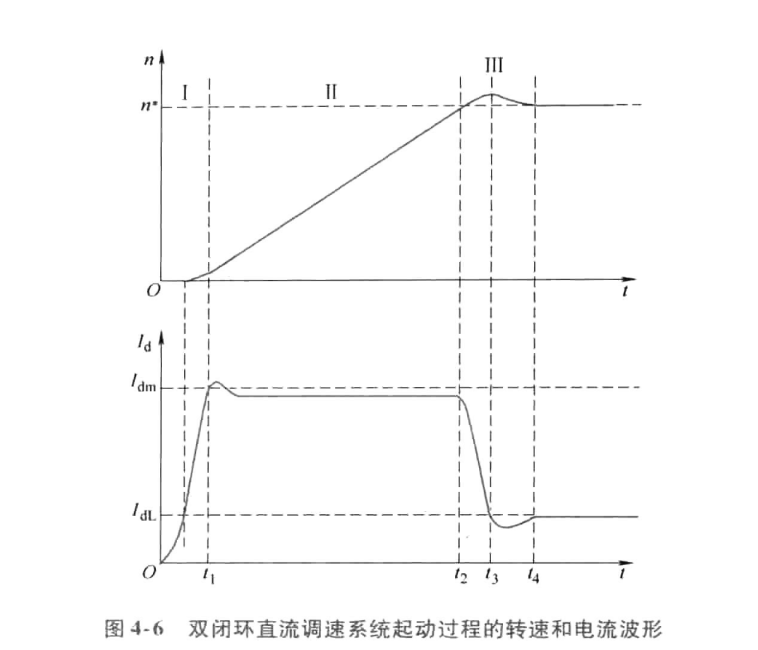


 准时间最优控制的定义
准时间最优控制的定义
在设备物理条件允许下实现最短时间的控制称作“时间最优控制”,对于调速系统,在电动机允许过载能力限制下的恒流起动,就是时间最优控制。但由于电感的作用,在电机加速和减速过程中,电机电流不能突变,所以实际起动过程与理想起动过程相比有一些差距,不过这两段时间只占全部起动时间中很小的成分,无伤大局,故称作“准时间最优控制”。
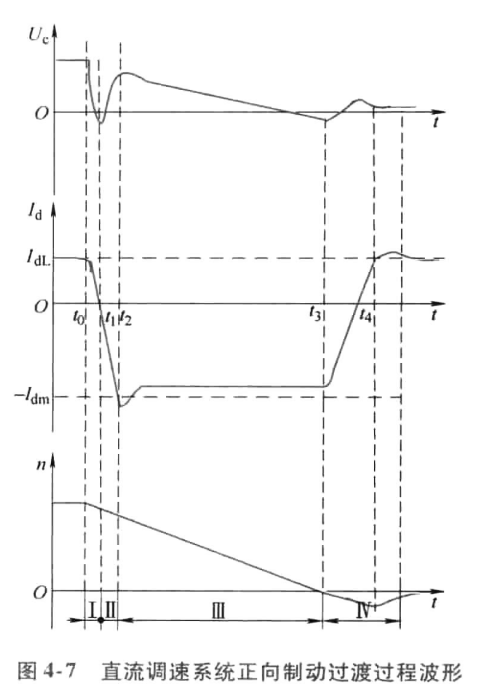
制动过程分析
与起动过程类似,可以把制动过程分为正向电流衰减、反向电流建立、恒流制动和转速调节四个阶段,转速调节器在此四个阶段中经历了不饱和、饱和以及退饱和三种情况。




总结
1.转速调节器的作用
1)转速调机器是调速系统的主导调节器,它使转速n很快地跟随转速给定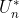 变化,稳态时可减少转速误差,如果采用PI调节器,则可实现无静差。
变化,稳态时可减少转速误差,如果采用PI调节器,则可实现无静差。
2)对负载变化起抗扰作用。
3)其输出限幅值决定电动机允许的最大电流。
2.电流调节器的作用
1)作为内环的调节器,在转速外环的调节过程中,它的作用是使电流紧紧跟随其给定电压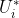 (外环调机器的输出量)变化。
(外环调机器的输出量)变化。
2)对电网电压的波动起及时抗扰的作用。
3)在转速动态过程中,保证获得电动机允许的最大电流,从而加快动态过程。
4)当电动机过载甚至堵转时,限制电枢电流的最大值,起快速的自动保护作用。一旦故障消失,系统自动恢复正常。安全保障对于系统的可靠运行来说是十分重要的。
4.3 双闭环调速系统的参数设计
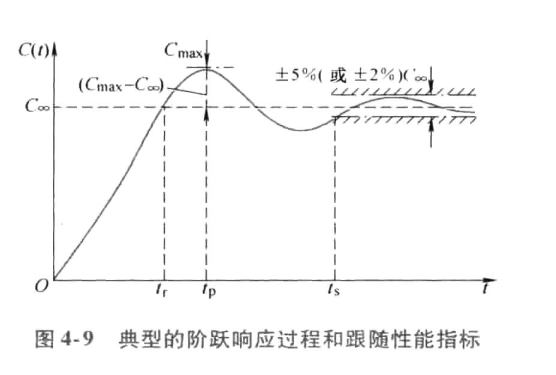
1.动态跟随性能指标
(1)上升时间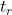
在跟随过程中,输出量从零起到第一次上升到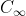 所经过的时间
所经过的时间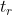 称作上升时间。它表示动态响应的快速性。
称作上升时间。它表示动态响应的快速性。
(2)超调量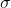 与峰值时间
与峰值时间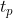
在阶跃响应过程中,超过上升时间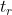 以后,输出量可能继续增加,到达最大值
以后,输出量可能继续增加,到达最大值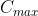 的时间称作峰值时间
的时间称作峰值时间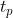 ,然后回落。
,然后回落。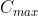 超过稳态值
超过稳态值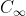 的百分数称作超调量,即
的百分数称作超调量,即
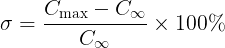
超调量反映系统的相对稳定性。超调量越小,相对稳定性越好。
(3)调节时间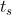
调节时间又称过渡过程时间,用来衡量输出量全部调节过程的快慢。理论上,线性系统的输出过渡过程要到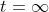 才稳定,为了在线性系统阶跃响应曲线上表示调节时间,认为稳态值
才稳定,为了在线性系统阶跃响应曲线上表示调节时间,认为稳态值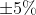 (或
(或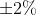 )的范围为允许误差带,以输出量达到并不再超出该误差带所需的时间定义为调节时间。显然,调节时间既反映了系统的快速性,也包含着它的稳定性。
)的范围为允许误差带,以输出量达到并不再超出该误差带所需的时间定义为调节时间。显然,调节时间既反映了系统的快速性,也包含着它的稳定性。
2.动态抗扰性能指标

在控制系统中,扰动量的作用点通常不同于给定量,因此系统抗扰的动态性能也不用于跟随的动态性能。在调速系统中主要扰动来源于负载扰动和电网电压波动。当调速系统在稳定运行中,突加一个使输出量降低(或上升)的扰动量F之后,输出量由开始降低(或升高)直到达到稳态值的过渡过程就是一个抗扰过程。常用的抗扰性能指标为动态降落和恢复时间。
(1)动态降落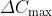
系统稳定运行时,突加一个约定的标准负扰动量,所引起的输出量最大降落值为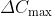 。
。
(2)恢复时间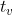
从阶跃扰动作用开始,到输出量基本上恢复稳态,距新稳态值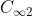 之差进入某基准量
之差进入某基准量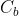 的
的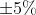 (或取
(或取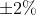 )范围之内所需的时间,定义为恢复时间
)范围之内所需的时间,定义为恢复时间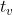 。
。
3.频域性能指标和伯德图
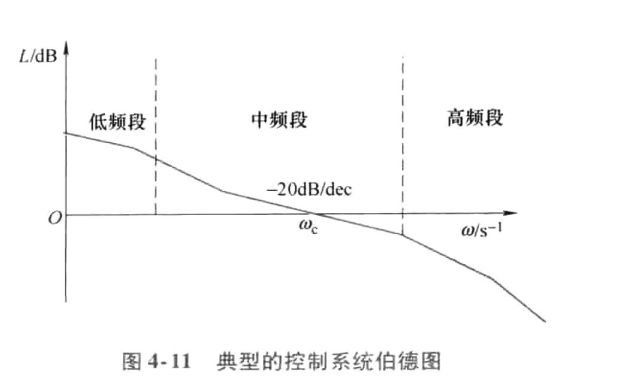
反映系统性能的伯德图特征有下列四个方面:
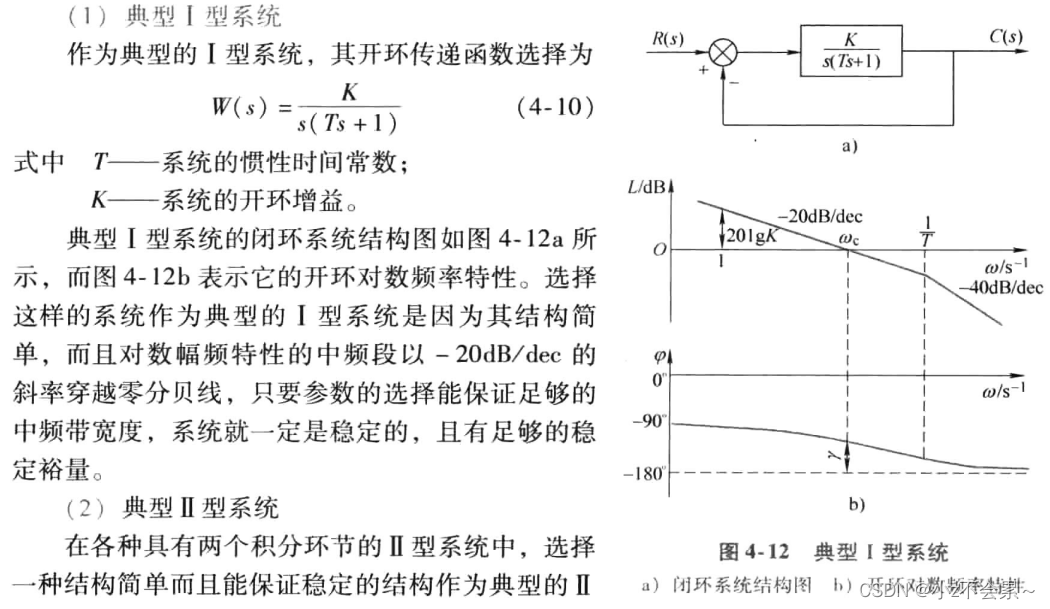
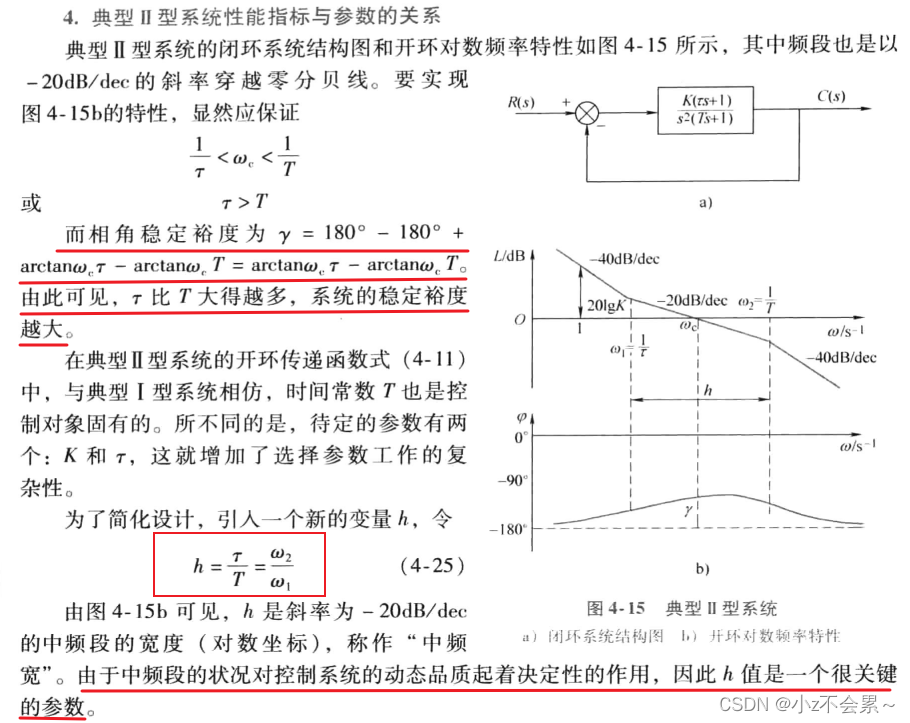
1)中频段以-20dB/dec的斜率穿越零分贝线,而且这一斜率占有足够的频带宽度,则系统的稳定性好。
2)截止频率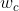 越高,则系统的快速性越好。
越高,则系统的快速性越好。
3)低频段的斜率陡、增益高,表示系统的稳态精度好(即静差率小、调速范围宽)。
4)高频段衰减得越快,即高频特性负分贝值越低,说明系统抗高频噪声干扰的能力越强。
以上四个方面常常是互相矛盾的。对稳态精度要求很高时,常需要放大系数大,可能使系统不稳定;增设校正装置使系统稳定,又可能牺牲快速性;提高截止频率可以加快系统的响应,又容易引入高频干扰;如此等等。应用线性系统控制理论进行设计时,往往需要多种手段反复试凑,在稳、准、快、抗干扰各方面取得折中,才能获得比较满意的结果。
4.4 调节器的工程设计方法





动态抗扰性能指标




动态抗扰性能指标
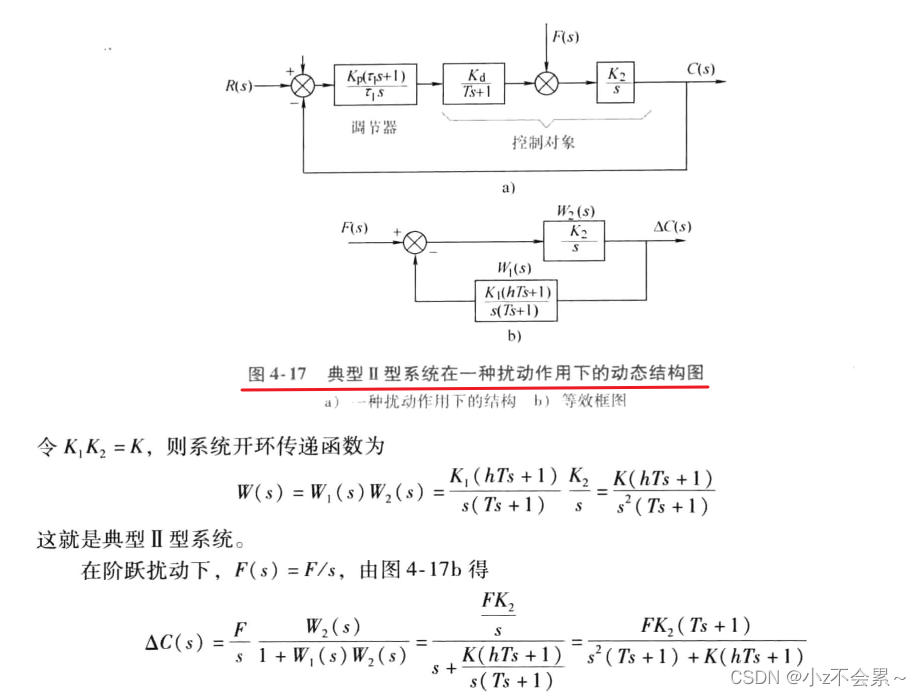


结论
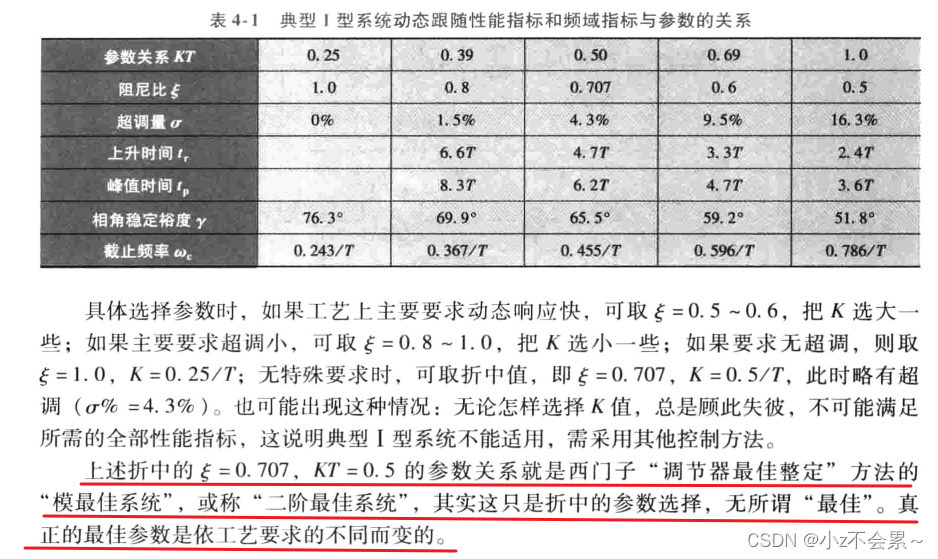
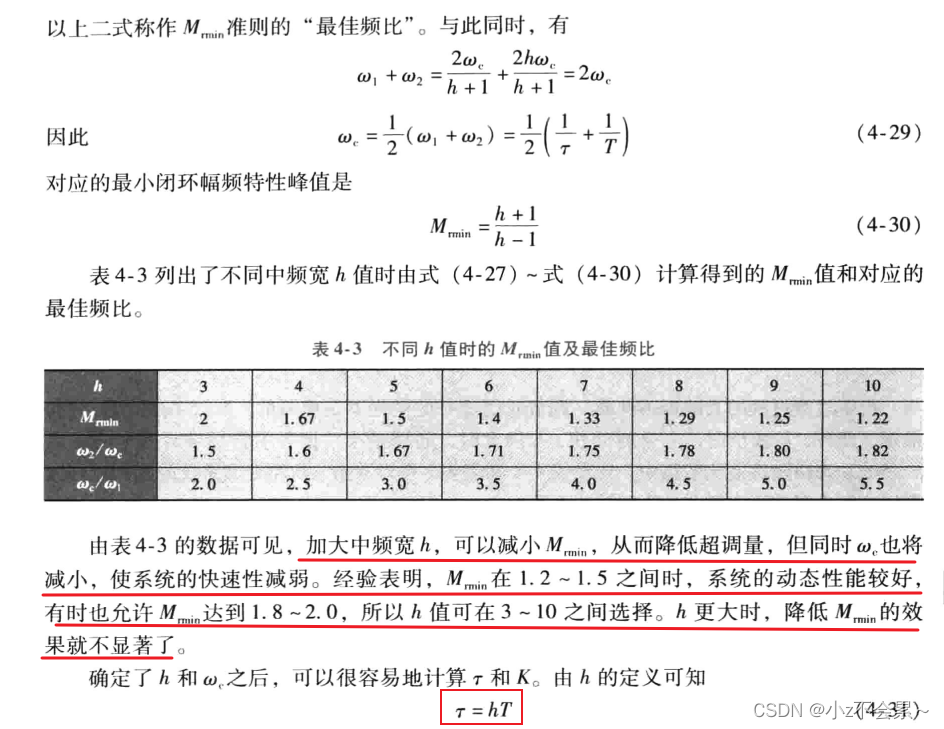
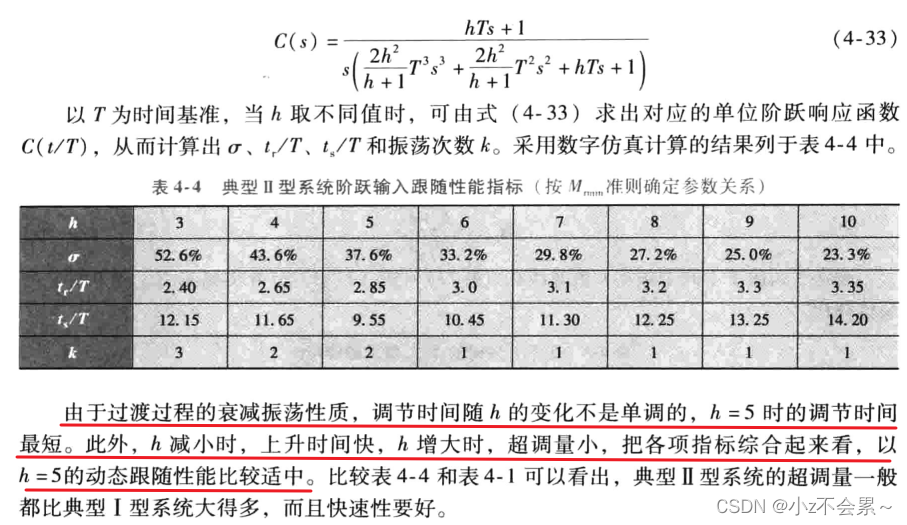
上述典型系统与参数的关系分析的比较详细,可以直接跳过看结论即可,这里直接给出一般情形下的较优参数,若按照典型i型系统进行参数最优调节,则取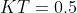 ,即
,即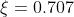 ,
,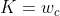 (当
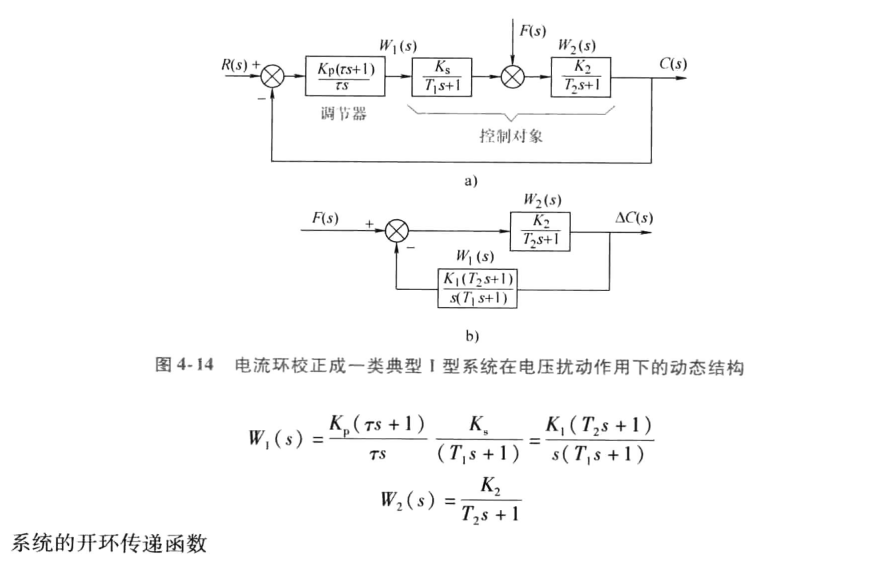
(当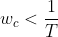 时)。若按照典型ii型系统进行参数最优调节,则取
时)。若按照典型ii型系统进行参数最优调节,则取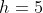 ,
,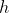 与
与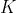 、
、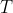 的关系为
的关系为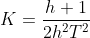 ,
,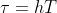 .
.
4.5 控制对象的工程近似处理方法
(1)高频段小惯性环节的近似处理

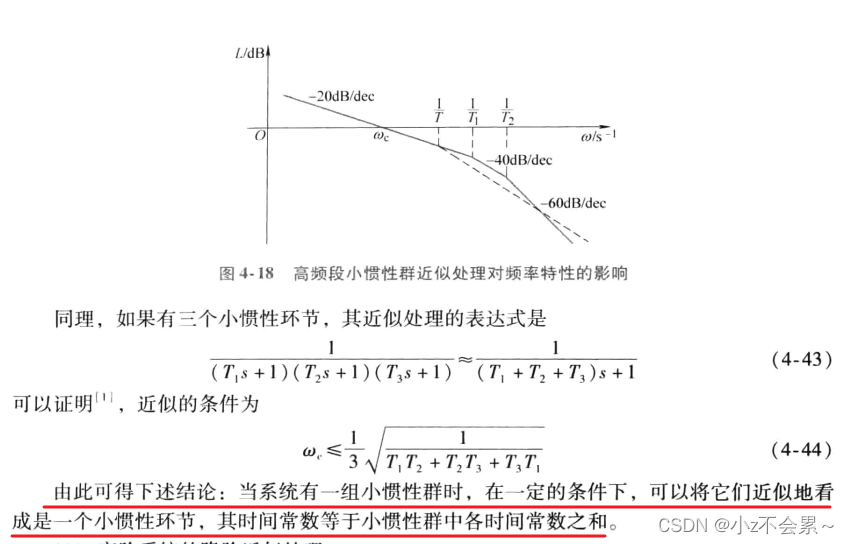
(2)高阶系统的降阶近似处理

(3)低频段大惯性环节的近似处理


以上内容均摘自《电力拖动自动控制系统》第四章,这里摘取了重点内容做一个汇总,方便以后自己查阅,感谢大家的阅读!!^_^