目录
1.遗传算法简要介绍
2.tsp问题简要介绍
3.遗传算法解决tsp问题的几个特殊点
4.源码
1.遗传算法简要介绍
简单来说,遗传算法是用于解决最优化问题的一种搜索算法。其核心基于自然界种群进化的规律,即初始种群进行交配,在基因层面上,其中会发生交叉互换、基因突变等变异,产生新一批的种群,在种群不断繁衍的过程中,“适者生存,不适者灭亡”,更符合环境要求的个体的基因保留下来的可能性更大,不适应环境的个体的基因往往不会延续下去。漫长的时间后,会筛选出一批最适应环境的种群。
基于此,当我们在解决最优化问题时,采取上述思想,将问题的解看作是“个体”,这些个体组成一个抽象的“种群”,这些解被映射成为相应的编码,于是我们就能得到由各种编码组成的“种群”。这些编码可以进行片段的交叉互换,或者其中某些数字发生“基因突变”,从而进行种群的更新。那么如何筛选更合适的个体呢?根据实际的需要与限制,我们基于编码,通过特定的函数,计算出每个个体的“适应度”,适应度更大的个体的基因(编码)被选中并保留下来的概率更大。这样经过上百次迭代后,就能得到一个接近最优解的一个种群。
详细的介绍大家可以参照这篇文章遗传算法详解 附python代码实现_重学CS的博客-CSDN博客_python遗传算法 ,文章作者将一般公式的最优化讲解到令人发指的详细与通俗易懂。如果能将这篇文章掌握,基本上可以通过遗传算法,求任何公式(n元n次方程)的最值。其中的内涵是将解从十进制数字映射成为二进制串,这其中的编码与解码过程很重要。
在这里就不展开叙述更多细节了,上面那篇文章讲的很清楚,本篇重点在于解决tsp问题。
2.tsp问题简要介绍
根据百度百科的介绍,t旅行商问题,即TSP问题(Traveling Salesman Problem)又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
3.遗传算法解决tsp问题的几个特殊点
这也是本篇的重点
3.1如何编码
首先要明白我们解的形式是什么,我们需要得到一条距离最短的路径。因此将这些城市编码(0、1、2........n),以10座城市为例,我们希望得到的解或许是3 5 4 8 6 7 9 0 2 1,因此,在遗传算法中,每个个体的形式就应该是10个不重复数字的排列。好消息是这样一来不需要进行二进制编码解码了。
#初始化种群def generate_population(self): path=np.array(range(self.num)) self.pop=[] for i in range(self.size_pop): x=path.copy() np.random.shuffle(x) #随机洗牌 self.pop.append(x)3.2距离矩阵的建立
我们该如何评价一个解的适应度?显然我们希望每个个体的路径距离越小越好,所以我们需要先得到每座城市之间的距离,将其记录在一个矩阵当中,当后续需要求一条完整路径的距离时,任意两点的距离可以直接转化为坐标(比如说,(2,6))从这个矩阵中取出。
3.3交叉互换
如果直接确定一条染色体上的一个位置,将父本母本从这个位置开始直接交叉互换,这显然是不合理的,假如父本是 1 3 2 4,母本是 2 4 1 3,两者正好在中点切割进行交叉互换后的子代分别是1 3 1 3和 2 4 2 4,这显然是错误的!旅行商每座城市只能经过一次!所以在交换染色体片段的时候,必须要经过一个操作,就是去除重复碱基对。
TSP、MTSP问题遗传算法详细解读及python实现,这篇文章的博主给出了tsp问题遗传算法交叉互换的三种方式,这里我们选择第二种
Order Crossover(顺序交叉)
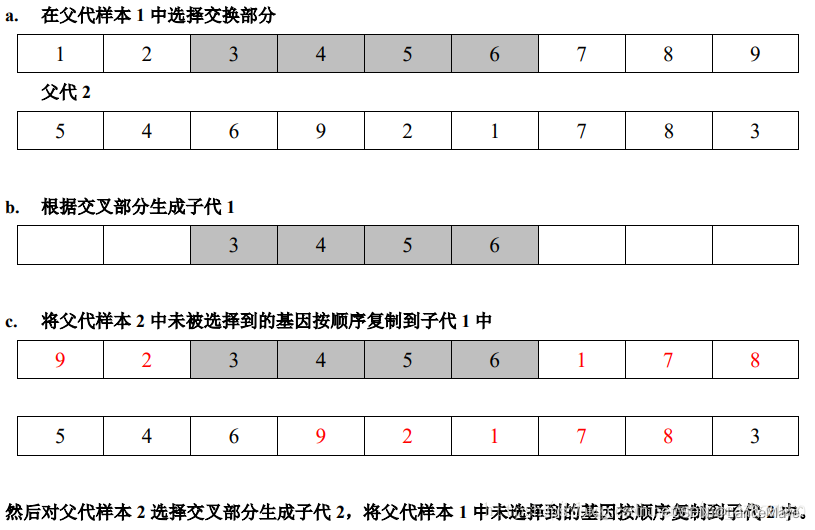
3.4基因突变
在二进制编码的情况下,要想完成基因突变,只需要将选中的染色体随机替换掉一个碱基对即可。但是在tsp问题中,如果这样做,一定会导致被选中染色体碱基对的重复!因此我们需要做的是将被选中染色体的任意两碱基对进行互换,这样就避免了重复
3.5适应度计算
我们该如何评价一个个体的基因是否适合被遗传下来呢?这就需要计算个体的适应度,适应度越高的个体,被选择的概率就越大。在tsp问题中,我们希望一个个体的路径长度越短越好,即路径越短,适应度越大,在这里,采用文章基于遗传算法求解TSP问题(旅游路径规划,Python实现,超详细,可视化,结果分析中的适应度公式来计算适应度
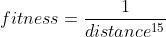
适应度越大的个体被选中的可能性越大,用numpy.choice来实现
idx = np.random.choice(np.arange(self.size_pop), size=self.size_pop, replace=True, p=(self.fitness)/(fitness_sum) )4.源码
import numpy as npclass TSP: def __init__(self, citys, maxgen=500, size_pop=200, cross_rate=0.8, muta_rate=0.005 ): self.maxgen = maxgen # 最大进化次数 self.size_pop = size_pop # 种群大小(染色体个数) self.cross_rate = cross_rate # 交叉概率 self.muta_rate = muta_rate # 变异概率 self.citys = citys # 城市的坐标数据 self.num = citys.shape[0] # 城市的个数(染色体长度) #获得距离矩阵 def matrix_distance(self): self.distance_m=np.zeros((self.num,self.num)) for i in range(self.num): for j in range(self.num): self.distance_m[i][j]=np.sqrt((self.citys[i][0]-self.citys[j][0])**2+(self.citys[i][1]-self.citys[j][1])**2) #计算某条路径的距离 def get_total_distance(self,one_path): distance=0 for i in range(self.num-1): distance +=self.distance_m[one_path[i]][one_path[i+1]] distance += self.distance_m[one_path[-1]][one_path[0]] return distance #初始化种群 def generate_population(self): path=np.array(range(self.num)) self.pop=[] for i in range(self.size_pop): x=path.copy() np.random.shuffle(x) #随机洗牌 self.pop.append(x) #交叉互换 def crossover(self): self.new_pop=[] for father in self.pop: child=father #初步让子代获得父本染色体 if np.random.rand()<self.cross_rate: #随机选择一个染色体作为母本 mother_index = np.random.randint(0, self.size_pop) mother=self.pop[mother_index] #确定切割点 left = np.random.randint(0, self.num-2) right = np.random.randint(left + 1, self.num-1) mother=mother.tolist() father=father.tolist() #切割片段 gene = mother[left:right] child1_c = father[right:]+father[:right] child1 = child1_c.copy() #去除重复基因 for o in gene: child1_c.remove(o) child1[left:right] = gene child1[right:] = child1_c[0:len(child1) - right] child1[:left] = child1_c[(len(child1) - right):] child=np.array(child1) self.new_pop.append(child) self.pop=self.new_pop #变异 def mutation(self): for i in range(self.size_pop): if np.random.rand() < self.muta_rate: child = self.pop[i] u = np.random.randint(0,self.num - 2) v = np.random.randint(u+1,self.num- 1) child_x = child[u+1:v] child_x=child_x[::-1] child = np.concatenate((child[0:u+1] , child_x , child[v:])) self.pop[i]=child #自然选择,种群根据适应度进行更新 def select(self): #计算每条路径的长度,放入列表 self.dis=[] for i in range(self.size_pop): self.dis.append(self.get_total_distance(one_path=self.pop[i])) #根据路径长度计算每个个体的适应度 self.fitness=[] for i in range(self.size_pop): self.fitness.append(1/(self.dis[i]**15)) #适应度总和 fitness_sum=0 for i in range(self.size_pop): fitness_sum+=self.fitness[i] #根据适应度进行选择,适应度大的被选择概率大 idx = np.random.choice(np.arange(self.size_pop), size=self.size_pop, replace=True, p=(self.fitness)/(fitness_sum) ) self.new_pop=[] for i in idx: self.new_pop.append(self.pop[i]) self.pop=self.new_pop #输出当前种群中最优路径 def result_path(self): self.index=np.argmax(self.fitness) a="the shortest path is:" for i in range(self.num-1): a+=str(self.pop[self.index][i]) a+="-->" a+=str(self.pop[self.index][-1]) print(a) print("the total distance is",self.dis[self.index]) #主函数进行迭代def main(citys): SL=TSP(citys) SL.matrix_distance() SL.generate_population() for i in range (SL.maxgen): SL.crossover() SL.mutation() SL.select() SL.result_path()if __name__ == '__main__': citys = np.array([[16.47, 96.10],[16.47, 94.44], [20.09, 92.54], [22.39, 93.37], [25.23, 97.24], [22.00, 96.05], [20.47, 97.02], [17.20, 96.29], [16.30, 97.38], [14.05, 98.12], [16.53, 97.38], [21.52, 95.59], [19.41, 97.13], [20.09, 92.55]]) main(citys)结果分析

如果每一次迭代都输出结果,可以清楚地看到路径最终都收敛。事实上,每次收敛的结果与种群大小size_pop息息相关,一开始我将种群大小设置为 200,结果每次运行虽然收敛,但是得到的结果各不相同,基本上毫无关联,说明结果陷入了局部最优解,而非全局最优解。解决方法就是把size_pop设置为500,才使得结果误差较小,趋近于全局最优解。
事实上,要想使结果更直观,最好用坐标图使结果可视化,将路线显示出来。本文仅仅展示了数字结果,这样有两个问题,一是可能起始城市不同,如8 2 3 6 和 2 3 6 8,二是顺序不同,如8 2 3 6和 6 3 2 8,其实结果的路线本质是一样的,但直观看上去不利于结果统计。
参考文章:
http://t.csdn.cn/eJZmK
http://t.csdn.cn/0fYtK
http://t.csdn.cn/VFPLr
http://t.csdn.cn/2oWZt