一、编程题
1.有假币
链接:有假币__牛客网 (nowcoder.com)
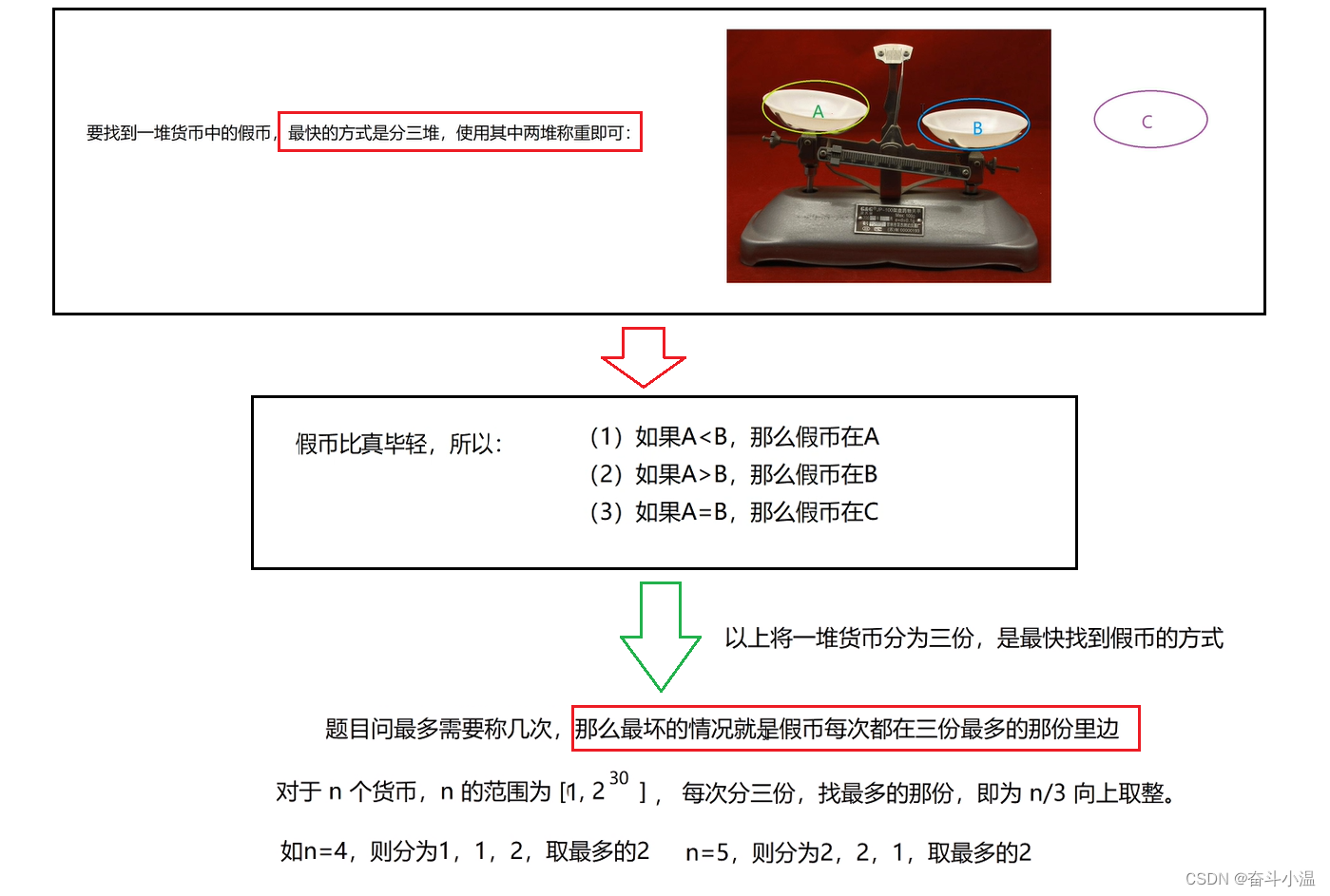
居然有假币! 现在猪肉涨了,但是农民的工资却不见涨啊,没钱怎么买猪肉啊。nowcoder这就去买猪肉,结果找来的零钱中有假币!!!可惜nowcoder 一不小心把它混进了一堆真币里面去了。只知道假币的重量比真币的质量要轻,给你一个天平(天平两端能容纳无限个硬币),请用最快的时间把那个可恶的假币找出来。
输入描述:
1≤n≤2^30,输入0结束程序。
输出描述:
最多要称几次一定能把那个假币找出来
示例1
输入
3
12
0
输出
1
3
?做题思路:

import java.util.Scanner;public class Main { public static void main(String[] args) { Scanner scanner = new Scanner(System.in); while (scanner.hasNext()) { int n = scanner.nextInt(); if (n == 0) { break; } int count = 0; while (n >= 2) { //注意的是Math返回的是double,强制转化为int n = (int) Math.ceil((double)n / 3); count++; } System.out.println(count); } }}2.正数数组的最小不可组成和
链接:求正数数组的最小不可组成和_百度笔试题_牛客网 (nowcoder.com)
给定一个全是正数的数组arr,定义一下arr的最小不可组成和的概念:
1️⃣arr的所有非空子集中,把每个子集内的所有元素加起来会出现很多的值,其中最小的记为min,最大的记为max;
2️⃣在区间[min,max]上,如果有一些正数不可以被arr某一个子集相加得到,那么这些正数中最小的那个,就是arr的最小不可组成和;
3️⃣在区间[min,max]上,如果所有的数都可以被arr的某一个子集相加得到,那么max+1是arr的最小不可组成和;
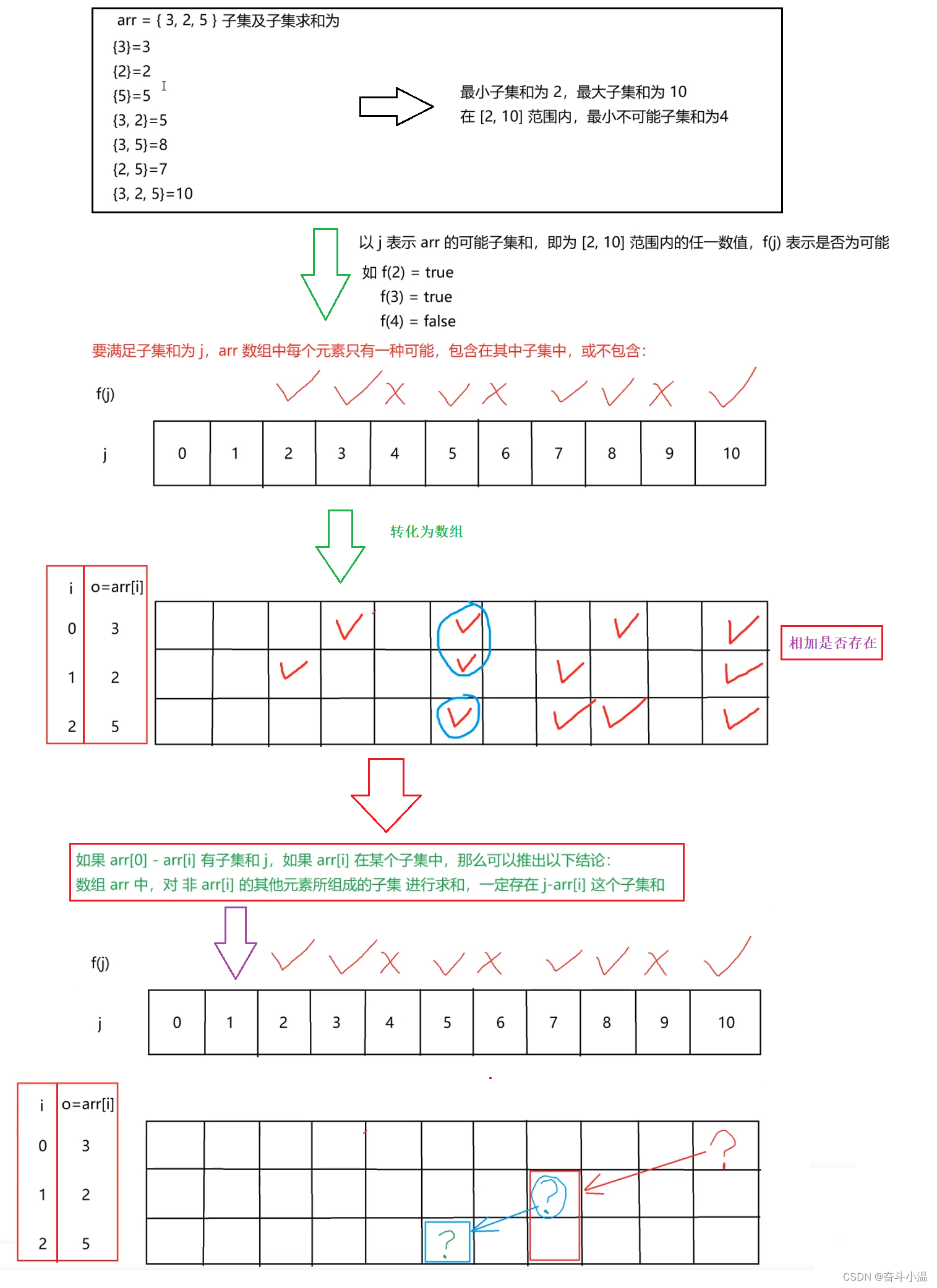
✨举例: arr = {3,2,5} arr的min为2,max为10,在区间[2,10]上,4是不能被任何一个子集相加得到的值中最小的,所以4是arr的最小不可组成和; arr = {3,2,4} arr的min为2,max为9,在区间[2,9]上,8是不能被任何一个子集相加得到的值中最小的,所以8是arr的最小不可组成和; arr = {3,1,2} arr的min为1,max为6,在区间[1,6]上,任何数都可以被某一个子集相加得到,所以7是arr的最小不可组成和; 请写函数返回arr的最小不可组成和。
?做题思路:
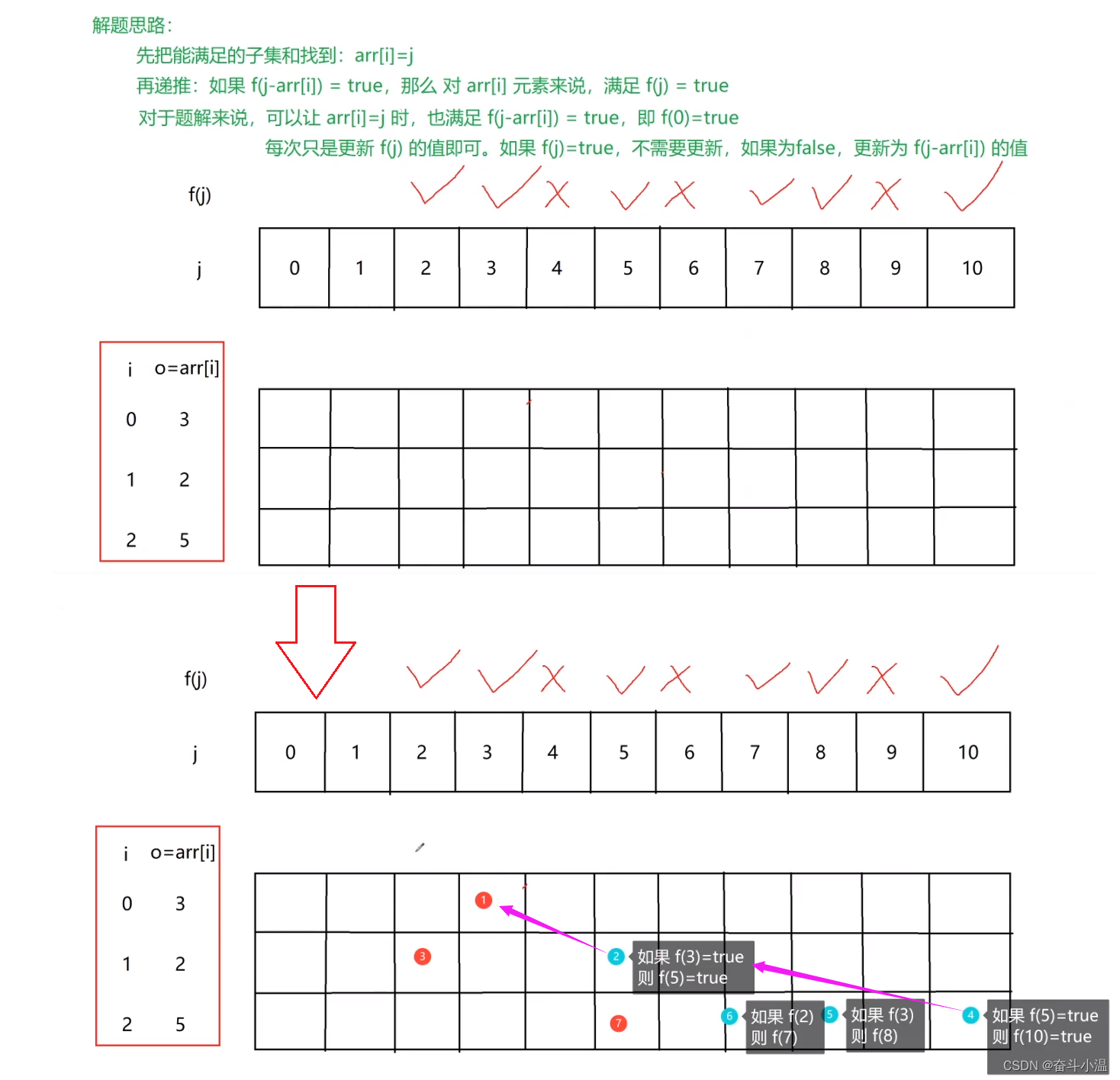
public class Solution {/** *正数数组中的最小不可组成和 *输入:正数数组arr *返回:正数数组中的最小不可组成和 */public int getFirstUnFormedNum(int[] arr) { int min = Integer.MAX_VALUE; int max = 0; for (int i = 0; i < arr.length; i++) { max += arr[i]; min = Math.min(min, arr[i]); } boolean result[] = new boolean[max + 1]; result[0] = true; // 为了使单个元素去求和时是真的 (i + 0 = i) for (int i = 0; i < arr.length; i++) { for (int j = max; j >= arr[i]; j--) { result[j] = result[j - arr[i]] || result[j]; } } for (int i = min; i < result.length; i++) { if (!result[i]) return i; } return max + 1; }}