文章目录
1、简介2、原理2.1 什么是注意力机制2.2 注意力机制在NLP中解决了什么问题2.3 注意力机制公式解读2.4 注意力机制计算过程 3、单头注意力机制与多头注意力机制4、代码4.1 代码14.2 代码2
1、简介
最近在学习transformer,首先学习了多头注意力机制,这里积累一下自己最近的学习内容。本文有大量参考内容,包括但不限于:
① 注意力,多注意力,自注意力及Pytorch实现
② Attention 机制超详细讲解(附代码)
③ Transformer 鲁老师机器学习笔记
④ transformer中: self-attention部分是否需要进行mask?
⑤ nn.Transformer Pytorch官方文档
⑥ The llustrated Transformer
⑦ 论文:Attention Is All You Need
⑧ attention-is-all-you-need-pytorch/transformer/SubLayers.py
⑨ Transformer、GPT、BERT,预训练语言模型的前世今生
2、原理
2.1 什么是注意力机制
重要性:Transformer、BETR等模型在NLP领域取得了重大突破,注意力机制(Attention Mechanism)起到了重要作用;注意力机制早在上世纪九十年代就有研究,2014年,Volodymyr在《Recurrent Models of Visual Attention》一文中将其应用在视觉领域,后来伴随着2017年Ashish Vaswani的《Attention is all you need》中Transformer结构的提出,注意力机制在NLP,CV相关问题的网络设计上被广泛应用。
"注意力机制"从名字中我们就可以看出关键在于注意力这个词,其实注意力在人身上能完美的体现,看下面这张狗的照片,大部分人的关注点儿都在狗和狗穿的衣服上,那么狗身后的背景往往被忽略,实际上注意力机制就是将人的注意力行为应用在机器上,让机器学会去感知数据中重要的和不重要的部分。还是以下图为例,进行狗识别的任务时,我们希望机器会更加关注重要部分(狗)而忽略不重要部分(背景)。

2.2 注意力机制在NLP中解决了什么问题
早期在解决机器翻译这一类序列到序列(Sequence to Sequence)的问题时,通常采用的做法是利用一个编码器(Encoder)和一个解码器(Decoder)构建端到端的神经网络模型,但是基于编码解码的神经网络存在两个问题,拿机器翻译举例:
问题1:如果翻译的句子很长很复杂,比如直接一篇文章输进去,模型的计算量很大,并且模型的准确率下降严重。
问题2:在翻译时,可能在不同的语境下,同一个词具有不同的含义,但是网络对这些词向量并没有区分度,无法结合词的上下文语境,导致翻译效果比较差。即无法解决词的多义(比如:”我在用苹果手机“和”这个苹果真好吃“这两个句子均出现苹果这个词,但是表达的意义完全不同)。
为了解决上述问题,注意力机制被提出。
2.3 注意力机制公式解读
我们首先以Transformer论文中的自注意力(Self-Attention)机制说起,Self-Attention的实现公式为:
这个公式中的Q、K和V分别代表Query、Key和Value,是三个矩阵。看到这里先不要着急,我们现在只需要知道自注意力机制中有这三个矩阵即可。
回顾一下向量点乘的几何意义:向量x在向量y方向上的投影再与向量y的乘积,能反映两个向量的相似度,且向量点乘的结果越大,两个向量越相似。
矩阵的每一行也可以看作是向量,如果一个矩阵 X 乘以其本身的转置 X T X^{\scriptscriptstyle T} XT,那么得到的结果不就能刻画该矩阵自身与自身的相似度吗?下面以词向量为例,这个矩阵中,每行为一个词的词向量。矩阵与自身的转置相乘,生成了目标矩阵,目标矩阵其实就是一个词的词向量与各个词的词向量的相似度。为了更清楚的表达,这里我引用鲁老师在transformer中的示例图片和代码:
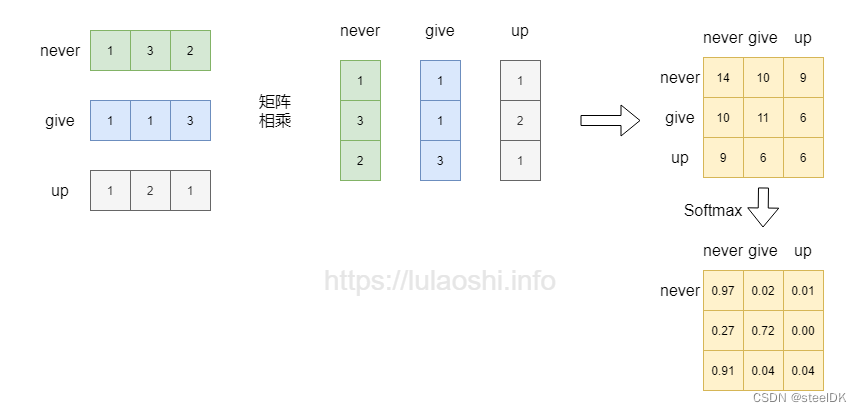
词向量相乘之后,如果再加上一个softmax,即softmax( X X T X^{T} XT)对向量相乘后的矩阵的每一行做归一化,那么就是对相似度的归一化,也就得到了一个归一化后的权重矩阵,这个矩阵中,数值越大代表相似度越大,比如never和never的相似度高达0.97。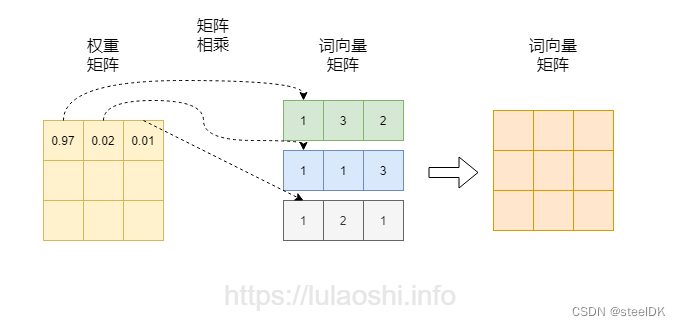
在图一的基础上,将softmax得到的权重矩阵与词向量相乘,如图二箭头所示。权重矩阵中某一行分别与词向量的一列相乘,词向量矩阵的一列其实代表着不同词的某一维度。经过这样一个矩阵相乘,相当于一个加权求和的过程,得到结果词向量是经过加权求和之后的新表示。
上述过程的Pytorch实现:
import torchimport torch.nn as nnx = torch.tensor([[1, 3, 2], [1, 1, 3], [1, 2, 1]], dtype=torch.float64)attention_scores = torch.matmul(x, x.transpose(-1, -2))attention_scores = nn.functional.softmax(attention_scores, dim=-1)print(attention_scores)有关与torch.matmul()相关函数的用法,可以参考:Pytorch教程之torch.mm、torch.bmm、torch.matmul、masked_fill。
2.4 注意力机制计算过程
在2.3中我们对矩阵乘法代表相似度的过程进行了初步了解,因此这里我们首先介绍一下自注意力机制公式中的矩阵Q、K、V是如何得到的。Transformer论文中将这个Attention公式描述为:Scaled Dot-Product Attention。其中,Q为Query、K为Key、V为Value。在Transformer的Encoder中所使用的Q、K、V其实都是从同样的输入矩阵X线性变换而来的,可以简单理解为: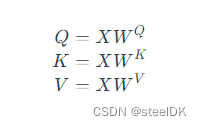
其中 W Q W^{Q} WQ、 W K W^{K} WK、 W V W^{V} WV是三个可训练的参数矩阵,输入矩阵X分别与 W Q W^{Q} WQ、 W K W^{K} WK、 W V W^{V} WV相乘,得到Q、K、V,相当于经过了一次线性变换。Attention不直接使用X,而是使用矩阵乘法生成这三个矩阵,这三个可训练的参数矩阵增强了模型的拟合能力。
Self-Attention计算过程如下:
第一步:X与W相乘,生成Q、K、V矩阵。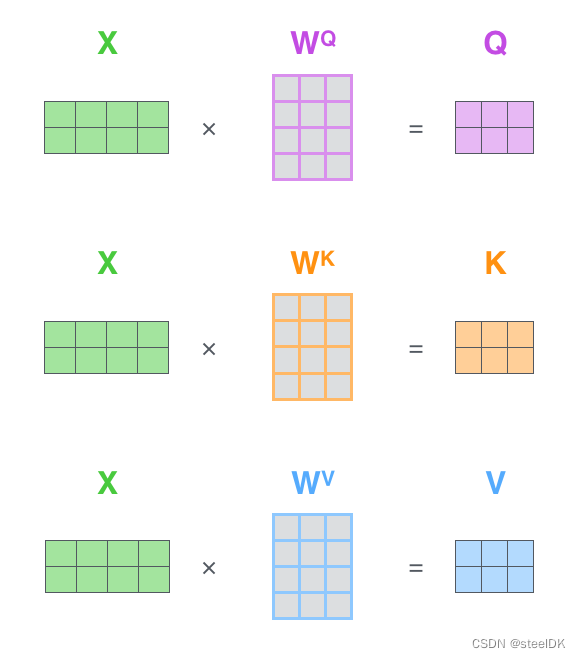
第二步:Q乘以 K T K^{T} KT,得到相似度。
比较经典的就是下图的示例,图片来源:The llustrated Transformer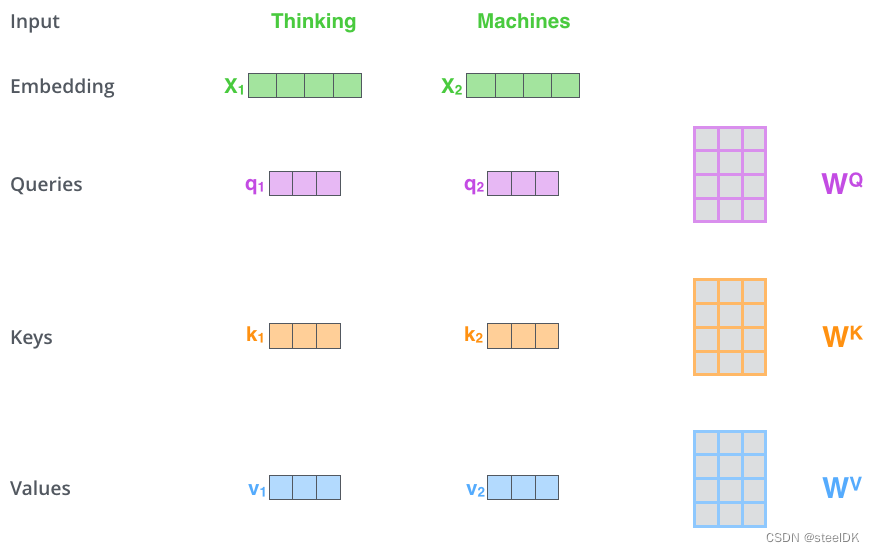
解读:假设有两个单词Thinking和Machines,这两个单词经过Embedding之后得到了代表这两个词的词向量X1和X2,如图四绿色所示。将这两个词向量X1和X2分别乘以矩阵 W Q W^{Q} WQ得到q1、q2查询向量,分别乘以 W K W^{K} WK得到k1、k2向量,分别乘以 W V W^{V} WV得到v1、v2向量,至此,代表这两个单词的q,k,v向量均已得到,接着就是计算两个词向量之间的相似度,如下图所示: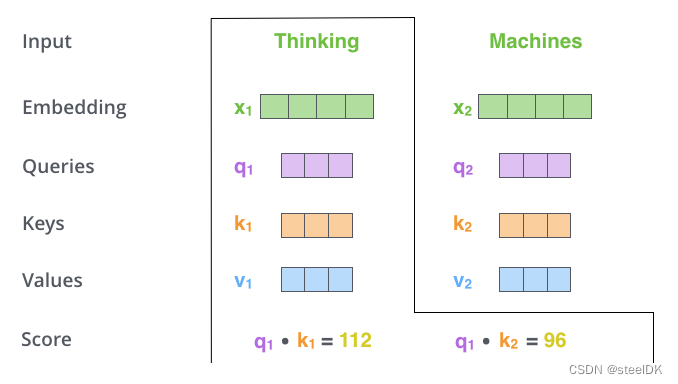
上图五演示的是代表单词Thinking的查询向量q1与自己的k1和单词Machines的k2分别相乘,得到Score,这里假设q1乘以k1的计算结果为112,q1乘以k2的计算结果为96,这两个结果就代表了单词Thinking与Thinking、单词Thinking与Machines之间的相似度。
第三步:将得到的相似度除以 d k \sqrt{d_k} dk ,然后进行softmax归一化,得到每个值都是大于0小于1的权重矩阵,且每行总和为1。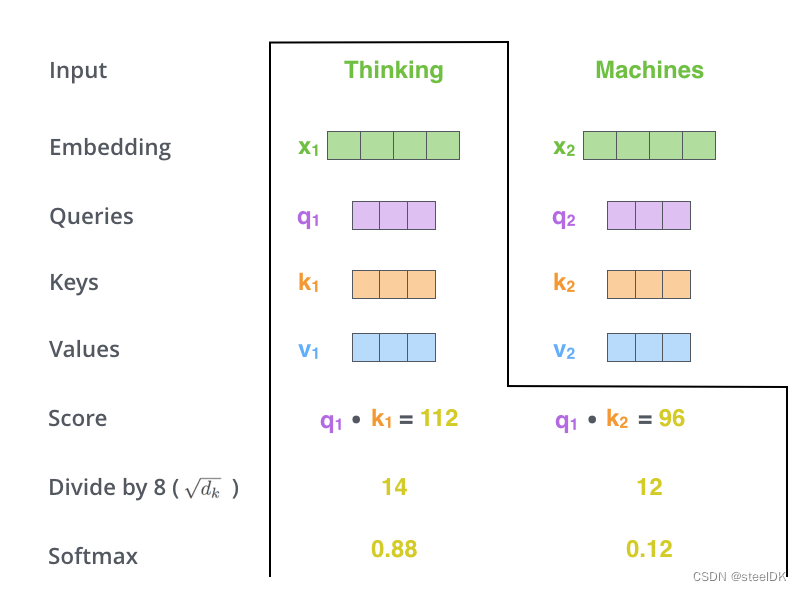
解读:在第三步中我们得到了相似度,即图中的Score,对两个单词的Score除以 d k \sqrt{d_k} dk ,然后进行softmax归一化, d k d_k dk是词向量x的维度,这里原文作者假设为64维了,所以开根号是8(不要计较文中所画X和q、k、v的维度数,仅仅是演示,知道计算流程即可)。通过softmax归一化之后,得到0.88和0.12,显然,和为1。
第四步:将第三步得到的权重矩阵与V相乘,进行加权求和。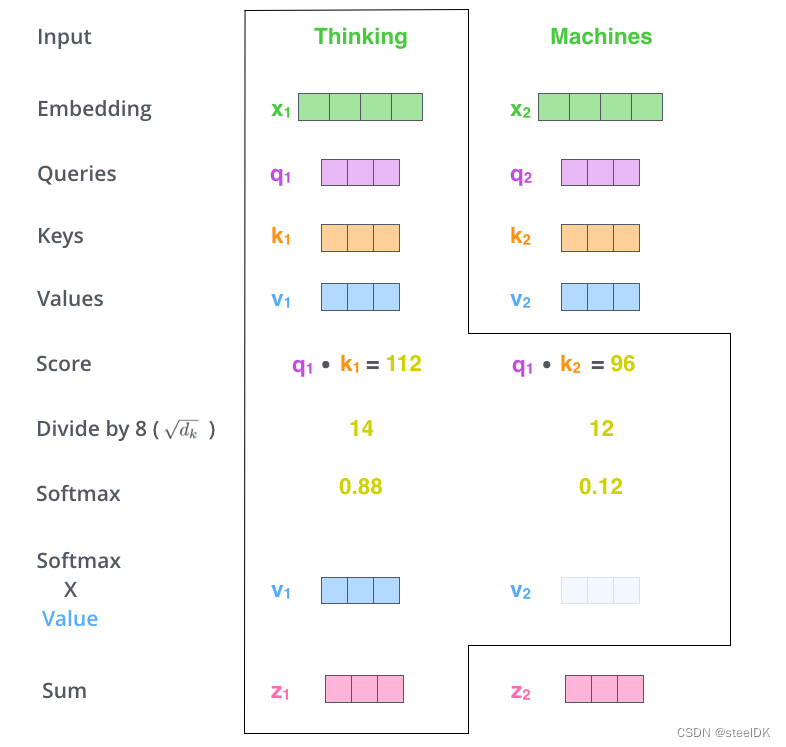
解读:将softmax得到的结果与与最开始得到v1和v2向量相乘,然后求和得到z1。注意,这几幅图都是以词Thingking为示例的,一个词向量得到一个z1。随后按照上述流程再计算词Machines与本身和Thingking之间相似度,最终经过softmax和Sum,同样得到z2。那么z1就代表了单词Thingking与这个句子中所有单词之间的关联,那么z2就代表了单词Thingking与这个句子中所有单词之间的关联。
仔细阅读会发现,我们上述所有的计算都是围绕着公式1进行的,下面给一个形象化的公式: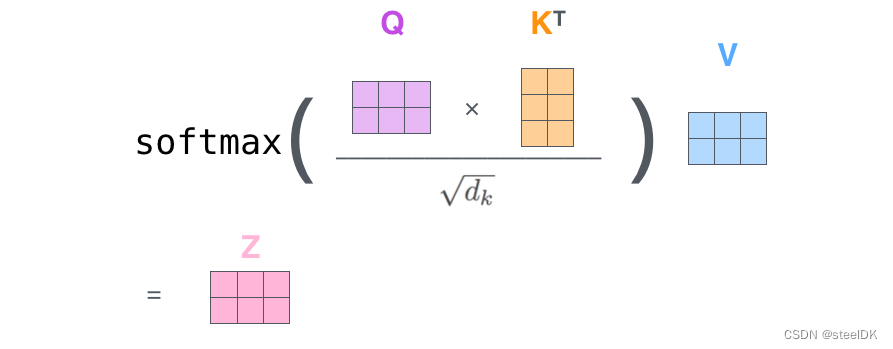
在获取了Q、K、V矩阵之后,主要进行的就是矩阵乘法。
3、单头注意力机制与多头注意力机制
在第二节当中,我们学习的都是单头注意力机制,在实际应用中,我们用的都是多头注意力机制,单头的意思是一个句子只有一组Q、K、V矩阵,多头的意思是在最开始生成Q、K、V矩阵的时候,同时生成多组Q、K、V矩阵,同时进行操作。我们以两组为例,示意图如下: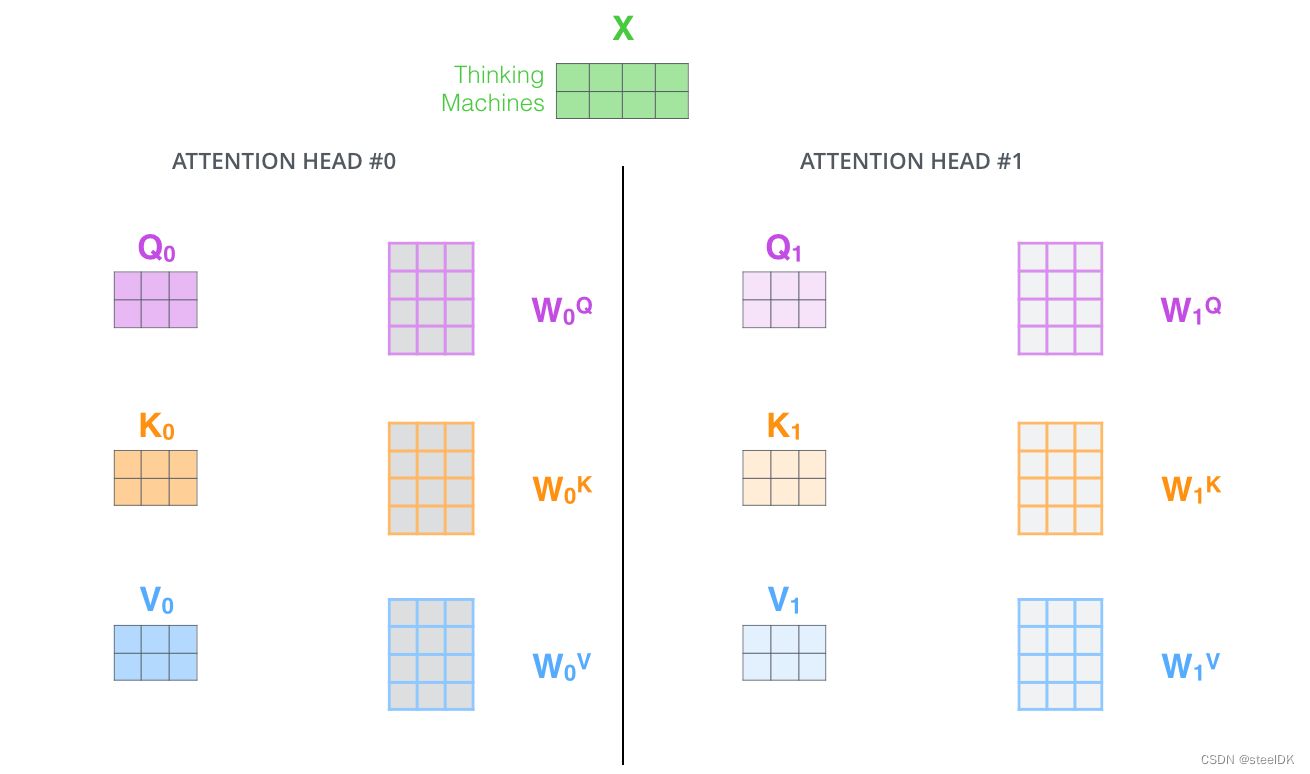
下面是一个8头的例子,计算流程如下: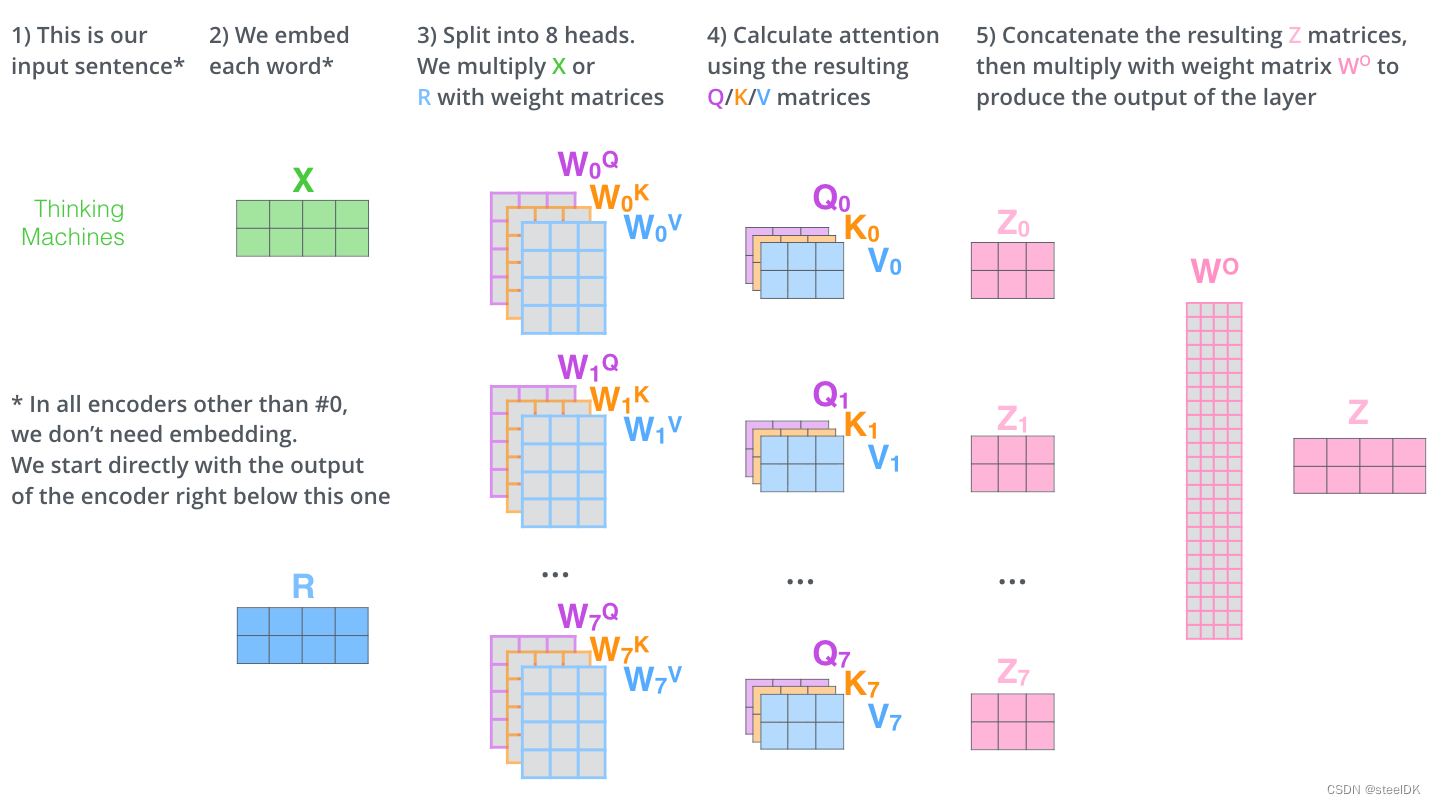
上图中的 W O W^{O} WO是output输出的权重的矩阵,目的是将前面8个头提取的信息进行汇总,是个在反向传播中需要更新的参数矩阵。
4、代码
4.1 代码1
此代码参考注意力,多头注意力,自注意力及Pytorch实现。
代码特点:直观、易于理解。
多头注意力代码是在单头注意力的基础上写成的,单头注意力的pytorch代码如下:
class ScaledDotProductAttention(nn.Module): """ Scaled Dot-Product Attention """ def __init__(self, scale): super().__init__() self.scale = scale self.softmax = nn.Softmax(dim=2) def forward(self, q, k, v, mask=None): u = torch.bmm(q, k.transpose(1, 2)) # 1.Matmul u = u / self.scale # 2.Scale if mask is not None: u = u.masked_fill(mask, -np.inf) # 3.Mask attn = self.softmax(u) # 4.Softmax output = torch.bmm(attn, v) # 5.Output return attn, outputif __name__ == "__main__": n_q, n_k, n_v = 2, 4, 4 d_q, d_k, d_v = 128, 128, 64 q = torch.randn(batch, n_q, d_q) k = torch.randn(batch, n_k, d_k) v = torch.randn(batch, n_v, d_v) mask = torch.zeros(batch, n_q, n_k).bool() attention = ScaledDotProductAttention(scale=np.power(d_k, 0.5)) attn, output = attention(q, k, v, mask=mask) print(attn) print(output)多头注意力机制的pytorch代码如下:
class MultiHeadAttention(nn.Module): """ Multi-Head Attention """ def __init__(self, n_head, d_k_, d_v_, d_k, d_v, d_o): super().__init__() self.n_head = n_head self.d_k = d_k self.d_v = d_v self.fc_q = nn.Linear(d_k_, n_head * d_k) self.fc_k = nn.Linear(d_k_, n_head * d_k) self.fc_v = nn.Linear(d_v_, n_head * d_v) self.attention = ScaledDotProductAttention(scale=np.power(d_k, 0.5)) self.fc_o = nn.Linear(n_head * d_v, d_o) def forward(self, q, k, v, mask=None): n_head, d_q, d_k, d_v = self.n_head, self.d_k, self.d_k, self.d_v batch, n_q, d_q_ = q.size() batch, n_k, d_k_ = k.size() batch, n_v, d_v_ = v.size() q = self.fc_q(q) # 1.单头变多头 k = self.fc_k(k) v = self.fc_v(v) q = q.view(batch, n_q, n_head, d_q).permute(2, 0, 1, 3).contiguous().view(-1, n_q, d_q) k = k.view(batch, n_k, n_head, d_k).permute(2, 0, 1, 3).contiguous().view(-1, n_k, d_k) v = v.view(batch, n_v, n_head, d_v).permute(2, 0, 1, 3).contiguous().view(-1, n_v, d_v) if mask is not None: mask = mask.repeat(n_head, 1, 1) attn, output = self.attention(q, k, v, mask=mask) # 2.当成单头注意力求输出 output = output.view(n_head, batch, n_q, d_v).permute(1, 2, 0, 3).contiguous().view(batch, n_q, -1) # 3.Concat output = self.fc_o(output) # 4.仿射变换得到最终输出 return attn, outputif __name__ == "__main__": n_q, n_k, n_v = 2, 4, 4 d_q_, d_k_, d_v_ = 128, 128, 64 q = torch.randn(batch, n_q, d_q_) k = torch.randn(batch, n_k, d_k_) v = torch.randn(batch, n_v, d_v_) mask = torch.zeros(batch, n_q, n_k).bool() mha = MultiHeadAttention(n_head=8, d_k_=128, d_v_=64, d_k=256, d_v=128, d_o=128) attn, output = mha(q, k, v, mask=mask) print(attn.size()) print(output.size())4.2 代码2
此代码参考attention-is-all-you-need-pytorch/transformer/SubLayers.py。
代码特点:实际应用中的代码,与代码1有些许差别
多头注意力代码是在单头注意力的基础上写成的,单头注意力的pytorch代码如下:
import torchimport torch.nn as nnimport torch.nn.functional as Fclass ScaledDotProductAttention(nn.Module): ''' Scaled Dot-Product Attention ''' def __init__(self, temperature, attn_dropout=0.1): super().__init__() self.temperature = temperature self.dropout = nn.Dropout(attn_dropout) def forward(self, q, k, v, mask=None): attn = torch.matmul(q / self.temperature, k.transpose(2, 3)) if mask is not None: attn = attn.masked_fill(mask == 0, -1e9) attn = self.dropout(F.softmax(attn, dim=-1)) output = torch.matmul(attn, v) return output, attn多头注意力机制的pytorch代码如下:
import numpy as npimport torch.nn as nnimport torch.nn.functional as class MultiHeadAttention(nn.Module): ''' Multi-Head Attention module ''' def __init__(self, n_head, d_model, d_k, d_v, dropout=0.1): super().__init__() self.n_head = n_head self.d_k = d_k self.d_v = d_v self.w_qs = nn.Linear(d_model, n_head * d_k, bias=False) self.w_ks = nn.Linear(d_model, n_head * d_k, bias=False) self.w_vs = nn.Linear(d_model, n_head * d_v, bias=False) self.fc = nn.Linear(n_head * d_v, d_model, bias=False) self.attention = ScaledDotProductAttention(temperature=d_k ** 0.5) self.dropout = nn.Dropout(dropout) self.layer_norm = nn.LayerNorm(d_model, eps=1e-6) def forward(self, q, k, v, mask=None): d_k, d_v, n_head = self.d_k, self.d_v, self.n_head sz_b, len_q, len_k, len_v = q.size(0), q.size(1), k.size(1), v.size(1) residual = q # Pass through the pre-attention projection: b x lq x (n*dv) # Separate different heads: b x lq x n x dv q = self.w_qs(q).view(sz_b, len_q, n_head, d_k) k = self.w_ks(k).view(sz_b, len_k, n_head, d_k) v = self.w_vs(v).view(sz_b, len_v, n_head, d_v) # Transpose for attention dot product: b x n x lq x dv q, k, v = q.transpose(1, 2), k.transpose(1, 2), v.transpose(1, 2) if mask is not None: mask = mask.unsqueeze(1) # For head axis broadcasting. q, attn = self.attention(q, k, v, mask=mask) # Transpose to move the head dimension back: b x lq x n x dv # Combine the last two dimensions to concatenate all the heads # together: b x lq x (n*dv) q = q.transpose(1, 2).contiguous().view(sz_b, len_q, -1) q = self.dropout(self.fc(q)) q += residual q = self.layer_norm(q) return q, attn后续会增加代码相关的解释。
待更~ 2023/04/07