
✨个人主页: 熬夜学编程的小林
?系列专栏: 【C语言详解】 【数据结构详解】
函数递归
1、递归是什么?
1.1、递归的思想
1.2、递归的限制条件
2、递归举例
2.1、举例1:求n的阶乘
2.1.1、分析和代码实现
2.1.2、画图推演
2.2、举例2:顺序打印⼀个整数的每⼀位
2.2.1、分析和代码实现
2.2.2、画图推演
3、递归与迭代
3.1、举例3:求第n个斐波那契数
总结
1、递归是什么?
递归是学习C语言函数绕不开的⼀个话题,那什么是递归呢? 递归其实是⼀种解决问题的⽅法,在C语言中,递归就是函数自己调⽤自己。 写⼀个史上最简单的C语⾔递归代码:#include <stdio.h>int main(){ printf("hehe\n"); main();//main函数中又调用了main函数 return 0;}
1.1、递归的思想
把⼀个大型复杂问题层层转化为⼀个与原问题相似,但规模较小的子问题来求解;直到子问题不能再被拆分,递归就结束了。所以递归的思考方式就是把 大事化小的过程。 递归中的 递就是递推的意思, 归就是回归的意思,接下来慢慢来体会。1.2、递归的限制条件
递归在书写的时候,有2个必要条件: • 递归存在限制条件,当满足这个限制条件的时候,递归便不再继续。 • 每次递归调用之后越来越接近这个限制条件。 在下面的例子中,我们逐步体会这2个限制条件。2、递归举例
2.1、举例1:求n的阶乘
⼀个正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,并且0的阶乘为1。 自然数n的阶乘写作n!。 题目:计算n的阶乘(不考虑溢出),n的阶乘就是1~n的数字累积相乘。2.1.1、分析和代码实现
我们知道n的阶乘的公式: n! = n ∗ ( n − 1)!举例: 5! = 5*4*3*2*1 4! = 4*3*2*1 所以:5! = 5*4!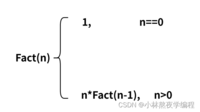 那我们就可以写出函数Fact求n的阶乘,假设Fact(n)就是求n的阶乘,那么Fact(n-1)就是求n-1的阶 乘,函数如下:
那我们就可以写出函数Fact求n的阶乘,假设Fact(n)就是求n的阶乘,那么Fact(n-1)就是求n-1的阶 乘,函数如下: int Fact(int n){ if(n==0) return 1; else return n*Fact(n-1);}#include <stdio.h>int Fact(int n){ if(n==0) return 1; else return n*Fact(n-1);}int main(){ int n = 0; scanf("%d", &n); int ret = Fact(n); printf("%d\n", ret); return 0;}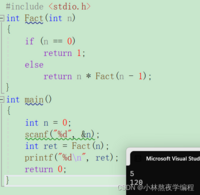
2.1.2、画图推演
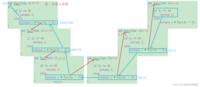 建议初次学习递归时画上述的递归展开图,更容易理解是如何进行递归的。
建议初次学习递归时画上述的递归展开图,更容易理解是如何进行递归的。 2.2、举例2:顺序打印⼀个整数的每⼀位
输⼊⼀个整数m,打印这个按照顺序打印整数的每⼀位。 比如: 输入:1234 输出:1 2 3 4 输入:520 输出:5 2 02.2.1、分析和代码实现
这个题目,放在我们面前,首先想到的是,怎么得到这个数的每⼀位呢? 如果n是⼀位数,n的每⼀位就是n自己; n是超过1位数的话,就得拆分每⼀位。 1234%10就能得到4,然后1234/10得到123,这就相当于去掉了4 然后继续对123%10,就得到了3,再除10去掉3,以此类推 不断的 %10 和 /10 操作,直到1234的每⼀位都得到; 但是这里有个问题就是得到的数字顺序是倒着的。 但是我们有了灵感,我们发现其实⼀个数字的最低位是最容易得到的,通过%10就能得到。 那我们假设想写⼀个函数Print来打印n的每⼀位,如下表示:Print(n)如果n是1234,那表示为Print(1234) //打印1234的每⼀位其中1234中的4可以通过%10得到,那么Print(1234)就可以拆分为两步:1. Print(1234/10) //打印123的每⼀位2. printf(1234%10) //打印4完成上述2步,那就完成了1234每⼀位的打印那么Print(123)⼜可以拆分为Print(123/10) + printf(123%10)以此类推下去,就有
Print(1234)==>Print(123) + printf(4)==>Print(12) + printf(3)==>Print(1) + printf(2)==>printf(1)直到被打印的数字变成⼀位数的时候,就不需要再拆分,递归结束。
那么代码完成也就比较清楚:
void Print(int n){if(n>9){Print(n/10);}printf("%d ", n%10);}int main(){int m = 0;scanf("%d", &m);Print(m);return 0;}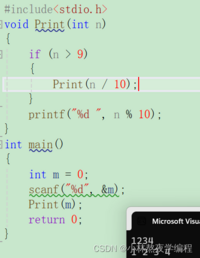 在这个解题的过程中,我们就是使用了 大事化小的思路 把Print(1234) 打印1234每⼀位,拆解为首先Print(123)打印123的每⼀位,再打印得到的4 把Print(123) 打印123每⼀位,拆解为首先Print(12)打印12的每⼀位,再打印得到的3 直到Print打印的是⼀位数,直接打印就行。
在这个解题的过程中,我们就是使用了 大事化小的思路 把Print(1234) 打印1234每⼀位,拆解为首先Print(123)打印123的每⼀位,再打印得到的4 把Print(123) 打印123每⼀位,拆解为首先Print(12)打印12的每⼀位,再打印得到的3 直到Print打印的是⼀位数,直接打印就行。 2.2.2、画图推演
以1234每⼀位的打印来推演⼀下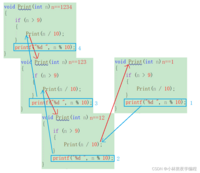
3、递归与迭代
递归是⼀种很好的编程技巧,但是很多技巧⼀样,也是可能被误用的,就像举例1⼀样,看到推导的公式,很容易就被写成递归的形式: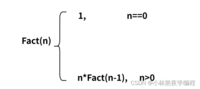
int Fact(int n){ if(n==0) return 1; else return n*Fact(n-1);}int Fact(int n){ int i = 0; int ret = 1; for(i=1; i<=n; i++) { ret *= i; } return ret;}3.1、举例3:求第n个斐波那契数
我们也能举出更加极端的例⼦,就像计算第n个斐波那契数,是不适合使用递归求解的,但是斐波那契数的问题通过是使⽤递归的形式描述的,如下: 看到这公式,很容易诱导我们将代码写成递归的形式,如下所示: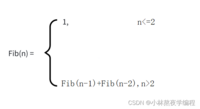
int Fib(int n){ if(n<=2) return 1; else return Fib(n-1)+Fib(n-2);}#include <stdio.h>int main(){ int n = 0; scanf("%d", &n); int ret = Fib(n); printf("%d\n", ret); return 0;}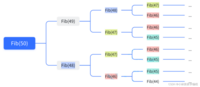 其实递归程序会不断的展开,在展开的过程中,我们很容易就能发现,在递归的过程中会有重复计 算,而且递归层次越深,冗余计算就会越多。我们可以做个测试:
其实递归程序会不断的展开,在展开的过程中,我们很容易就能发现,在递归的过程中会有重复计 算,而且递归层次越深,冗余计算就会越多。我们可以做个测试: #include <stdio.h>int count = 0;int Fib(int n){ if(n == 3) count++;//统计第3个斐波那契数被计算的次数 if(n<=2) return 1; else return Fib(n-1)+Fib(n-2);}int main(){ int n = 0; scanf("%d", &n); int ret = Fib(n); printf("%d\n", ret); printf("\ncount = %d\n", count); return 0;}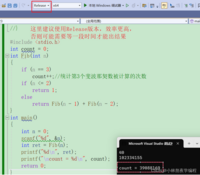 这里我们看到了,在计算第 40个斐波那契数的时候,使用递归方式,第3个斐波那契数就被重复计算了 39088169次,这些计算是非常冗余的。所以斐波那契数的计算,使用递归是非常不明智的,我们就得想迭代的方式解决。 我们知道斐波那契数的前2个数都1,然后前2个数相加就是第3个数,那么我们从前往后,从小到大计算就行了。 这样就有下面的代码:
这里我们看到了,在计算第 40个斐波那契数的时候,使用递归方式,第3个斐波那契数就被重复计算了 39088169次,这些计算是非常冗余的。所以斐波那契数的计算,使用递归是非常不明智的,我们就得想迭代的方式解决。 我们知道斐波那契数的前2个数都1,然后前2个数相加就是第3个数,那么我们从前往后,从小到大计算就行了。 这样就有下面的代码: int Fib(int n){ int a = 1; int b = 1; int c = 1; while(n>2) { c = a+b; a = b; b = c; n--; } return c;}总结
本篇博客就结束啦,谢谢大家的观看,如果公主少年们有好的建议可以留言喔,谢谢大家啦!