蓝桥杯考前必看知识点【python 代码详解】

文章目录

前言一、基本知识点1.基本输入输出2.列表转字符串3.字符串大小写转换4.匿名函数lambda5.二/八/十六进制6.chr/ord转换7.保留小数点后几位8.排序 二、python常用内置库模块1.factorial阶乘2.Counter计数器3.defaultdict默认字典4.deque双向队列5.permutation全排列6.combinations组合7.accumulate累加8.heapq堆9.datetime时间 三、常用算法模板1.最大公约数 / 最小公倍数2.质数判断 / 质数个数3.快速幂4.bisect二分 总结

---

前言

最近一直在准备蓝桥杯，看了很多知识点及模板，考前几天就来个总结笔记巩固一下吧。写的还是比较全面的，希望也能帮助到其他备考的小伙伴呀>_<。

---

一、基本知识点

1.基本输入输出

s = input()  # 一个字符串n = int(input())  # 单个数a, b, c = map(int, input().split())  # 多个数l_1 = list(map(int, input().split()))  # 整个列表（空格分隔）l_2 = [int(i) for i in input().split()]  # 整个列表（空格分隔，和上一个差不多）print(s, n, a, b, c)print(l_1, l_2)"""输入如下：abc101 2 34 5 61 2 3 5 6输出如下：abc 10 1 2 3[4, 5, 6] [1, 2, 3, 5, 6]"""

2.列表转字符串

l_3 = ['a', 'b', 'c']print(''.join(l_3))  # 输出结果：abc

3.字符串大小写转换

a = "abcd"b = "ABCD"print(a.upper(), b.lower())  # ABCD abcdprint(a, b)  # abcd ABCD

4.匿名函数lambda

lambda的“：”左边是输入右边是输出，尤其和排序函数放在一起真的很好用啊！

def square(a):    return a ** 2print(list(map(square, [1, 2, 3])))  # [1, 4, 9]print(list(map(lambda x: x ** 2, [1, 2, 3])))  # [1, 4, 9]h = [[2, 4],     [8, 9],     [4, 5],     [5, 10]]print(sorted(h, key=lambda x: x[0], reverse=True))  # 按照每个列表的第一个元素倒序排序# [[8, 9], [5, 10], [4, 5], [2, 4]]

5.二/八/十六进制

print(hex(17), oct(9), bin(3))  # 0x11 0o11 0b11print(int('11', 2), int('11', 8), int('11', 16))  # 3 9 17

6.chr/ord转换

ord()就是得到字符的ASCII值，chr()是通过ASCII值找到字符。

print(chr(97), ord('a'))  # a 97

7.保留小数点后几位

整理了三种方法如下：

x = 1.321print(round(x, 2))  # 1.32print('%.2f' % x)  # 1.32print('{:.2f}'.format(x), f'{x:.2f}')  # 1.32 1.32

8.排序

nums.sort()：在原列表上直接排序sorted(nums)：不改动原列表，生成新列表

nums = [5, 2, 7, 1, 3]nums1 = sorted(nums, reverse=True)  # 倒序print(nums1)  # [7, 5, 3, 2, 1]nums.sort()print(nums)  # [1, 2, 3, 5, 7]

二、python常用内置库模块

1.factorial阶乘

可以使用factorial阶乘求排列组合的结果（不要忘了import math）：

def c(m, n):  # 是在m个数中取出n个    return math.factorial(m) // (math.factorial(n) * math.factorial(m-n))print(c(5, 2))  # 10print(math.factorial(5))  # 120

2.Counter计数器

使用计数器可以直接算出每个元素出现的次数，就不需要我们遍历啦。需要获得列表的话，直接在前面套一个list()就可以了。

from collections import Counterl2 = ['a', 'b', 'b', 'c', 'c', 'c']d1 = Counter(l2)print(d1)  # 输出结果：Counter({'c': 3, 'b': 2, 'a': 1})d1['d'] = 1  # 加一个键值对print(d1)  # 输出结果：Counter({'c': 3, 'b': 2, 'a': 1, 'd': 1})print(list(d1))  # 输出结果：['a', 'b', 'c', 'd']print(d1.keys())  # dict_keys(['a', 'b', 'c', 'd'])print(d1.values())  # dict_values([1, 2, 3, 1])print(d1.items())  # dict_items([('a', 1), ('b', 2), ('c', 3), ('d', 1)])

3.defaultdict默认字典

我们用哈希表计数的时候，若当前元素不存在，则置为1；但是用defaultdict直接+1就行，不需要判断，因为创建defaultdict的时候已经规定了默认值类型。

from collections import defaultdictd2 = defaultdict(int)  # 默认是int型，就默认值为0for i, x in enumerate(l2):    d2[x] += 1  # 省去一步判断存在的情况print(list(d2.items()))  # [('a', 1), ('b', 2), ('c', 3)]print(d2['a'], d2['d'])  # 1 0

4.deque双向队列

找到一张对双向队列解释的非常好的图片（原文在这里）：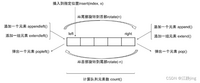

from collections import dequed3 = deque([1, 2, 3], maxlen=4)  # 初始化一个最大长度为maxlen的队列d3.append(4)print(d3)  # deque([1, 2, 3, 4], maxlen=4)d4 = deque()  # 初始化一个无固定长度的队列d4.append(1)  # 添加元素到队尾d4.append(2)d4.append(3)d4.appendleft(0)  # 添加元素到队首print(d4, list(d4))  # deque([0, 1, 2, 3]) [0, 1, 2, 3]print(d4.popleft(), d4.pop())  # 弹出队首/队尾元素 0 3print(d4)  # deque([1, 2])

5.permutation全排列

from itertools import permutationsl1 = list(permutations([1, 2, 3]))print(l1)  # [(1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1)]

6.combinations组合

from itertools import combinationsl3 = list(combinations([1, 2, 3], 2))  # 第二个参数为选择组合的个数print(l3)  # [(1, 2), (1, 3), (2, 3)]

7.accumulate累加

accumulate在求前缀和时很好用，不需要自己遍历一遍数组了。
accumulate函数创建一个迭代器，返回累积汇总值或其他双目运算函数的累积结果值（通过可选的 func 参数指定）。如果提供了 func，它应当为带有两个参数的函数但是，如果提供了关键字参数 initial，则累加会以 initial值开始，这样输出就比输入的可迭代对象多一个元素。

from itertools import accumulatea = [1, 2, 3, 4]print(list(accumulate(a)))  # [1, 3, 6, 10]print(list(accumulate(a, initial=0)))  # [0, 1, 3, 6, 10]print(list(accumulate(a, initial=1)))  # [1, 2, 4, 7, 11]

8.heapq堆

python中的堆是小顶堆，如果是二维列表，默认以每个列表的第一个元素来排序。
1）heapify让列表具有堆的特征；
2）heappop弹出最小的元素（总是位于索引0处）；
3）heappush用于在堆中添加一个元素；
4）从堆中弹出最小的元素，再压入一个新元素。

from heapq import *h = [[2, 4],     [8, 9],     [4, 5],     [5, 10]]heapify(h)print(h)  # [[2, 4], [5, 10], [4, 5], [8, 9]]print(heappop(h))  # [2, 4]print(h)  # [[4, 5], [5, 10], [8, 9]]heappush(h, [1, 2])print(h)  # [[1, 2], [4, 5], [8, 9], [5, 10]]heapreplace(h, [3, 2])print(h)  # [[3, 2], [4, 5], [8, 9], [5, 10]]print(heappop(h))  # [3, 2]

9.datetime时间

差点忘了这个，时间模块之前也是经常考的。

from datetime import *start = date(year=2023, month=4, day=4)end = date(year=2023, month=4, day=8)t = timedelta(days=1)while start <= end:    print(start, start.weekday())  # 0-6 代表周一到周日    start += tprint(end.year, end.month, end.day)"""2023-04-04 12023-04-05 22023-04-06 32023-04-07 42023-04-08 52023 4 8"""

---

三、常用算法模板

1.最大公约数 / 最小公倍数

最大公约数在math中可以写，也可以直接使用math.gcd(x, y)调用，调用的时候不要忘了import math :

import mathdef gcd(n1, n2):  # 自己写    if n2 > n1:        n1, n2 = n2, n1    while n2:        n1, n2 = n2, n1 % n2        print(n1, n2)    return n1    # return math.gcd(n1, n2) if n2 > 0 else n1  # 调用# print(gcd(6, 81))

最小公倍数就是两数乘积再除以最大公约数：

def lcm(n1, n2):    return n1 * n2 // gcd(n1, n2)    # return n1 * n2 // math.gcd(n1, n2)# print(lcm(6, 81))

2.质数判断 / 质数个数

判断数n是否为质数：

def isPrim(n):    if n < 2:        return False    for i in range(2, int(n ** 0.5) + 1):        if n % i == 0:            return False    return True# print(isPrim(7))

判断1到n之间（不包括n这个数）有多少个素数（厄拉多塞筛法）：

def countPrim(n):    count = 0    signs = [True] * n  # 先假设全为质数    for i in range(2, n):        if signs[i]:            count += 1            for j in range(i+i, n, i):  # 质数的倍数一定不是质数，置为False                signs[j] = False    return count# print(countPrim(5))  # 2 3

3.快速幂

参考了一位大佬的文章，想深入了解戳这里哦，一步一步带你去理解，真的写的非常非常好！

def normalPower(base, power):    result = 1    while power:        if power % 2 == 1:            result = result * base % 1000        base = base * base % 1000        power //= 2    return result# print(normalPower(2, 1000000000))

4.bisect二分

其实这一部分也可以放在上面内置模块部分。二分法当然可以自己写的，但是现成的库是真好用啊，做题时省时省力！
1)查找：
bisect：查找目标元素右侧插入点
bisect_left：查找目标元素左侧插入点
bisect_right：查找目标元素右侧插入点
2)插入：
insort：查找目标元素右侧插入点，并保序地插入元素
insort_left： 查找目标元素左侧插入点，并保序地插入元素
insort_right：查找目标元素右侧插入点，并保序地插入元素

from bisect import *l4 = [1, 2, 3, 3, 3, 4, 5]pos = bisect(l4, 3)  # 只查找，不改变列表pos_left = bisect_left(l4, 3)pos_right = bisect_right(l4, 3)print(pos, pos_left, pos_right)  # 5 2 5insort(l4, 4.5)print(l4)  # [1, 2, 3, 3, 3, 4, 4.5, 5]insort(l4, 2.5)print(l4)  # [1, 2, 2.5, 3, 3, 3, 4, 4.5, 5]

总结

好啦，今天就暂时到这里了，要是再想起什么我会继续补充的。如果大家发现有不妥之处或者有想补充的，欢迎留言哦。