MATLAB的小波分析工具箱(Wavelet Toolbox)为工程师和科学家提供了广泛的算法和应用来分析和处理信号和图像。该工具箱提供了一系列小波转换和小波分析函数,包括连续小波变换(CWT)、离散小波变换(DWT)、最大重叠离散小波变换(MODWT)等。
以下是一些主要的功能:
小波变换:小波变换包括连续小波变换(CWT)和离散小波变换(DWT)。连续小波变换可以提供信号的时间-尺度表示,离散小波变换可以将信号分解成不同频率的子带。
小波分解与重构:可以使用wavedec和waverec等函数进行小波分解和重构,这对于信号和图像的多分辨率分析与处理非常有用。
降噪与压缩:提供了一系列降噪和压缩函数,如wdencmp(进行小波分解的阈值压缩)、wden(自适应小波降噪)等。
特征提取:可以通过小波变换提取信号或图像的特征,例如findpeaks可以寻找模极大值。
小波族:提供了多种类型的小波函数,如Daubechies、Symlets、Coiflets等,并且允许用户自定义小波函数。
wavedec函数是MATLAB中的一个函数,用于计算一维信号的离散小波变换。它的输出参数 C 和 L 分别表示小波系数向量和书签向量。
C(小波系数向量):这是一个一维数组,其中包含了所有级别的详细系数和最后级别的近似系数。C的长度等于信号的长度加上滤波器长度减1,乘以分解级别。C的内容按照从低级别到高级别的顺序排列,即第1级详细系数,第2级详细系数,…,最后级别的详细系数,最后级别的近似系数。
L(书签向量):这是一个一维数组,其中包含了C中每一级的详细系数和近似系数的长度。L的长度等于分解级别加2。L的内容按照从高级别到低级别的顺序排列,即最后级别的近似系数长度,最后级别的详细系数长度,…,第1级详细系数长度,信号长度。
在MATLAB中,你可以使用wavedec函数进行小波分解,然后使用waverec函数进行重构,从而得到每一级小波分解的结果。
MATLAB代码:
clear all;clc;close all;
% snr=100;
% init=256;
% [xref,x]=wnoise(2,10,snr,init);
% signal=x;
N=1024;
t=linspace(0,6*pi,N)';
signal=5*sin(t)+rand(N,1);
% 选择小波基函数和分解级别
waveletFunction = 'db4';
level = 5;
% 进行小波分解
[C,L] = wavedec(signal,level,waveletFunction);%
% 重构信号
reconstructedSignal = waverec(C,L,waveletFunction);
% 画图对比原始信号和重构信号
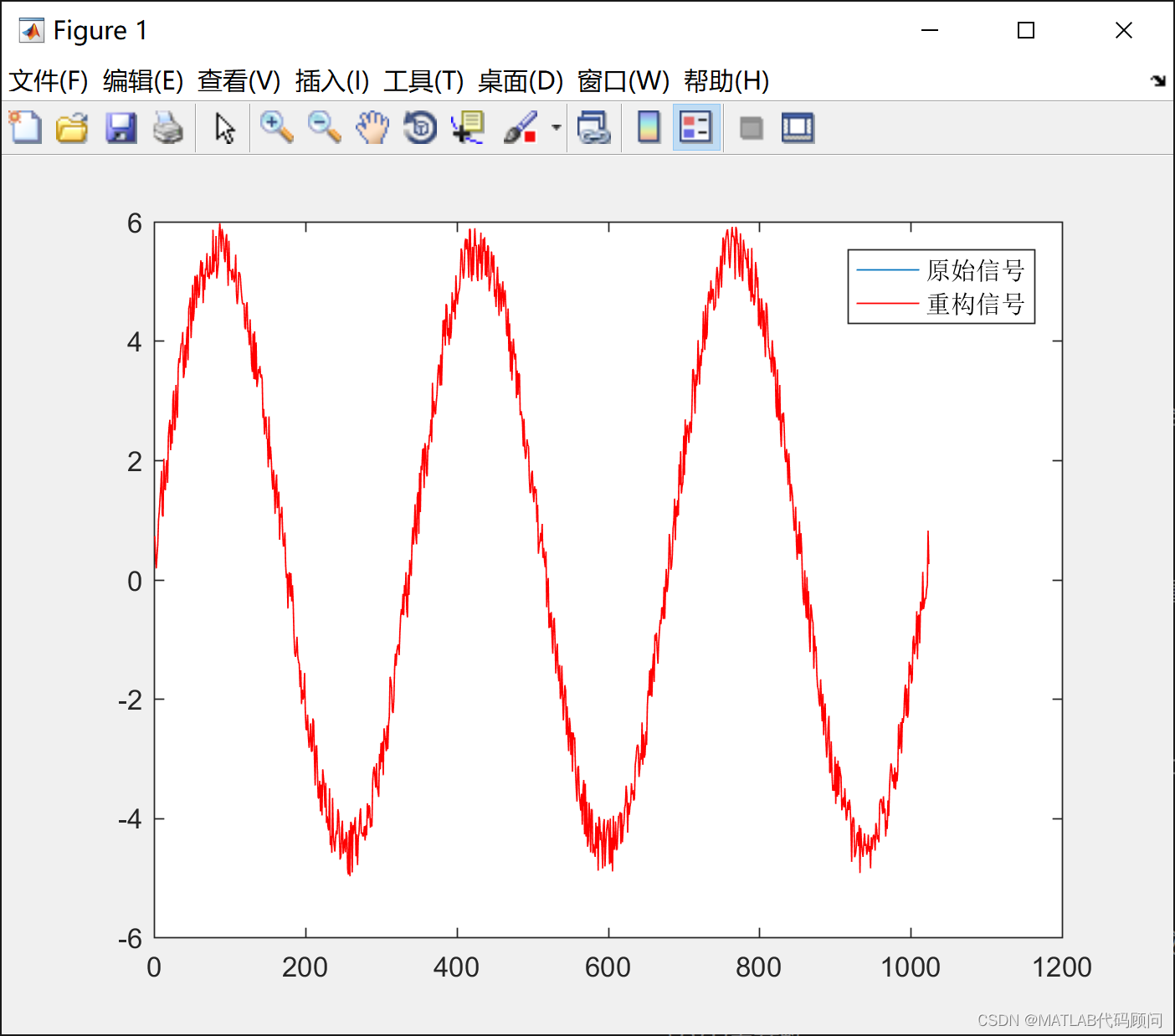
figure;
plot(signal);
hold on;
plot(reconstructedSignal,'r');
legend('原始信号','重构信号');
% 绘制小波分解
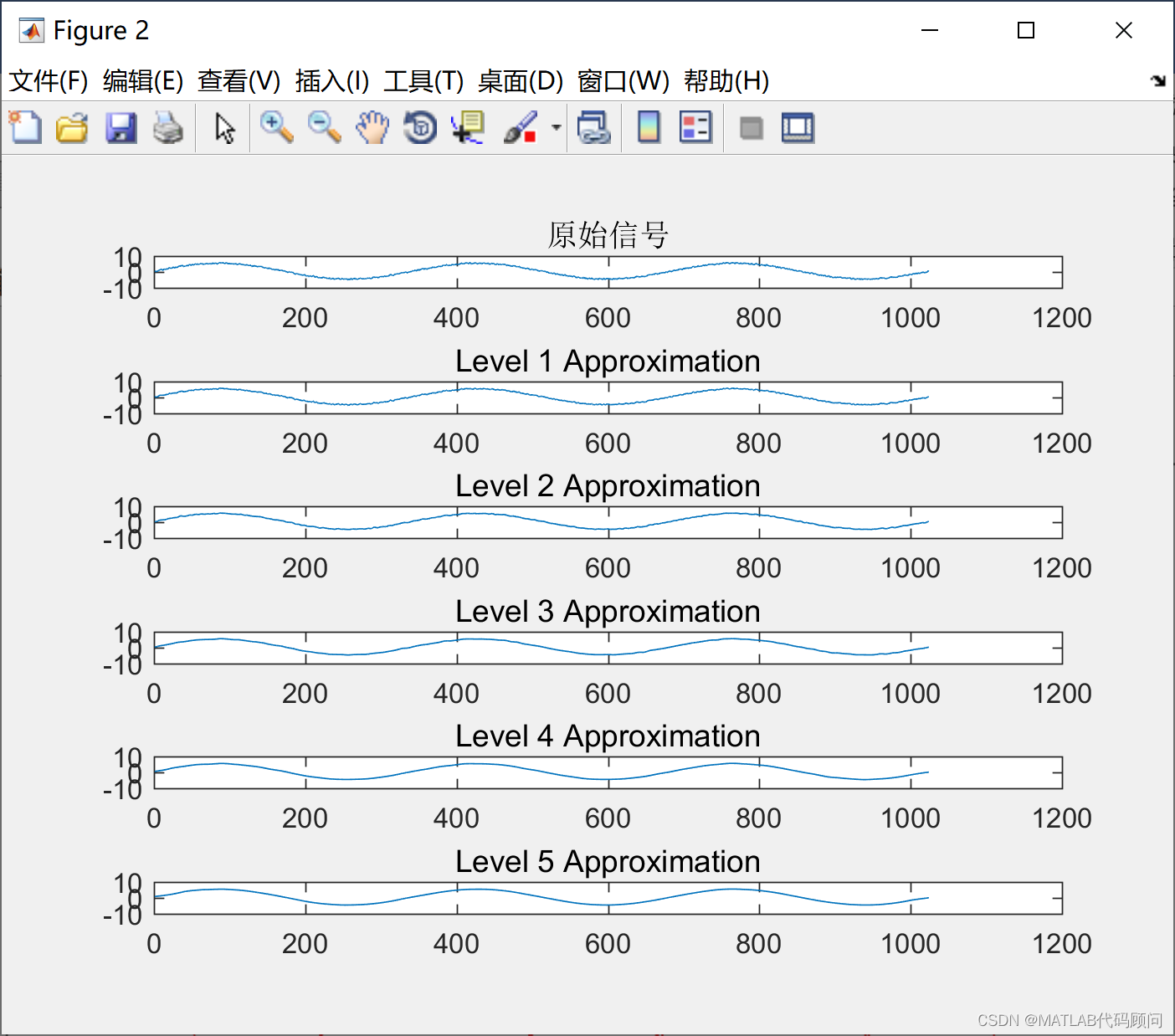
figure;
% 显示原始信号
subplot(level+1, 1, 1);
plot(signal);
title('原始信号');
% 重构并显示每一级的小波分解结果
for i = 1:level
% 重构近似系数或细节系数
A = wrcoef('a',C,L,waveletFunction,i);
D = wrcoef('d',C,L,waveletFunction,i);
% 显示近似系数
subplot(level+1, 1, i+1);
plot(A);
title(['Level ', num2str(i), ' Approximation']);
% 显示细节系数(如果需要的话)
% subplot(level+2, 1, i*2+1);
% plot(D);
% title(['Level ', num2str(i), ' Detail']);
end
figure;
plot(reconstructedSignal-signal);
%% 降噪与压缩
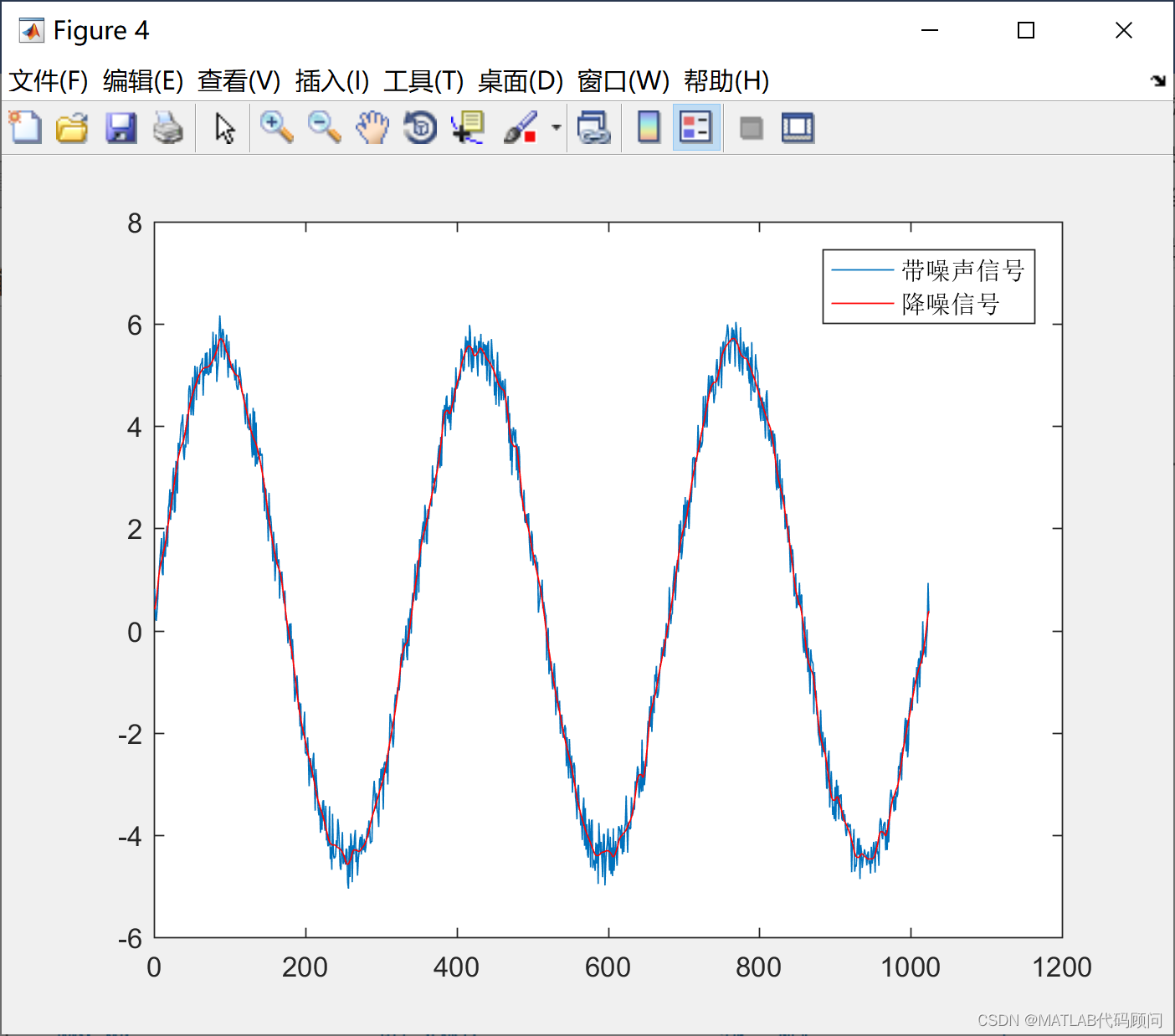
noisySignal =signal + randn(size(signal))*0.1;
% 选择小波基函数和分解级别
waveletFunction = 'db4';
level = 3;
% 进行小波降噪
denoisedSignal = wden(noisySignal,'heursure','s','one',level,waveletFunction);
% 画图对比原始信号和降噪后的信号
figure;
plot(noisySignal);
hold on;
plot(denoisedSignal,'r');
legend('带噪声信号','降噪信号');
%% 特征提取
% 选择小波基函数和分解级别
waveletFunction = 'db4';
level = 3;
% 进行小波分解
[C,L] = wavedec(signal,level,waveletFunction);
% 提取各级细节系数
for i = 1:level
details{i} = detcoef(C,L,i);
end
% 找到最大的细节系数
maxDetailCoef = max(cellfun(@max,details));
% 显示最大的细节系数
disp('最大的细节系数:');
disp(maxDetailCoef);
程序结果:
最大的细节系数:
0.7735
>>