文章目录
一、直观理解决策树二、熵的作用三、信息增益四、决策树构造实例4.1 问题描述4.2 根节点构造 五、信息增益率和GINI系数5.1 信息增益存在的问题5.2 信息增益率5.3 GINI系数 六、连续值特征划分七、剪枝方法(预剪枝和后剪枝)八、回归问题预测思路九、Python代码实现决策树9.1 导入所需要的库9.2 构建数据集9.3 函数编写9.4 测试算法效果 十、SkLearn库实现决策树并可视化10.1 Graphviz可视化库安装10.2 树模型的可视化展示10.3 预剪枝参数及作用分析10.3.1 预剪枝参数介绍10.3.2 预剪枝参数作用 10.4 对数据的敏感性分析10.5 回归任务
一、直观理解决策树
决策树即通过一步步决策得到最终结果的树
如下图所示,如果要判断一个人在家庭里的身份,我们可以先判断ta年龄是否大于15,如果是,则说明ta是爷爷或奶奶或妈妈,如果不是,则再判断ta是否为男性,如果是,则ta是儿子,否则ta是女儿。
这就是一个决策树的基本流程。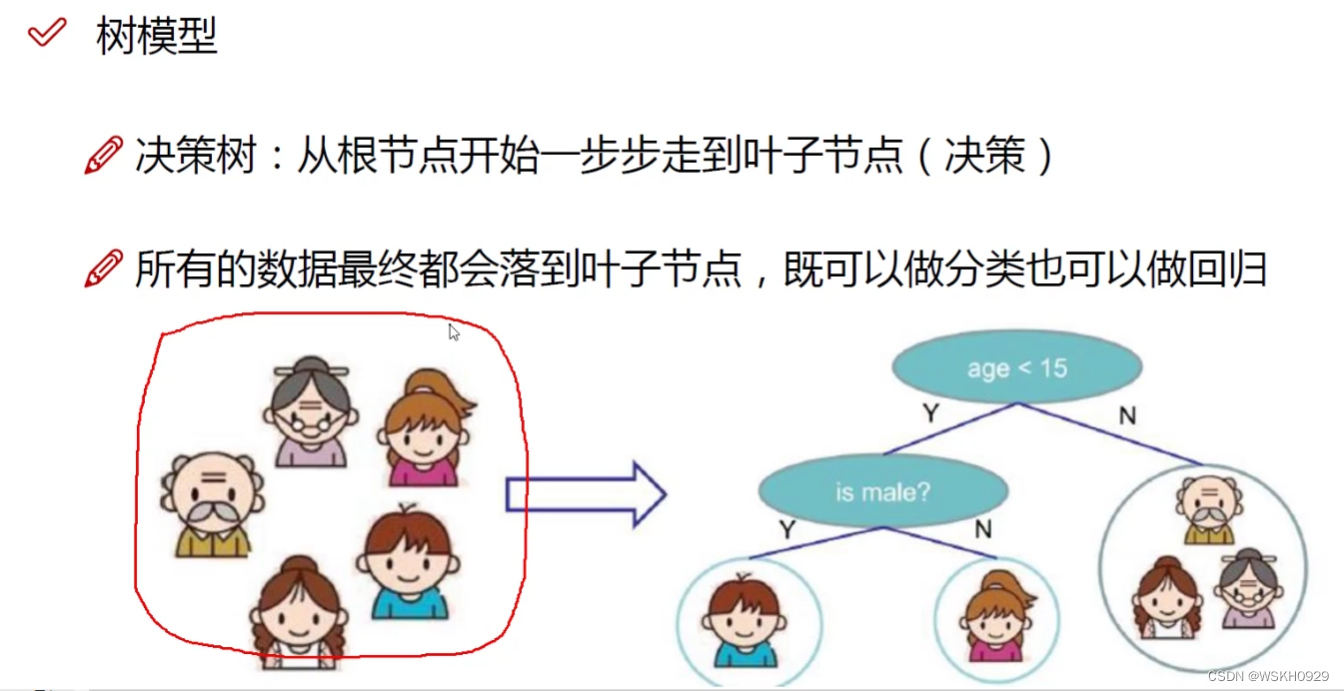
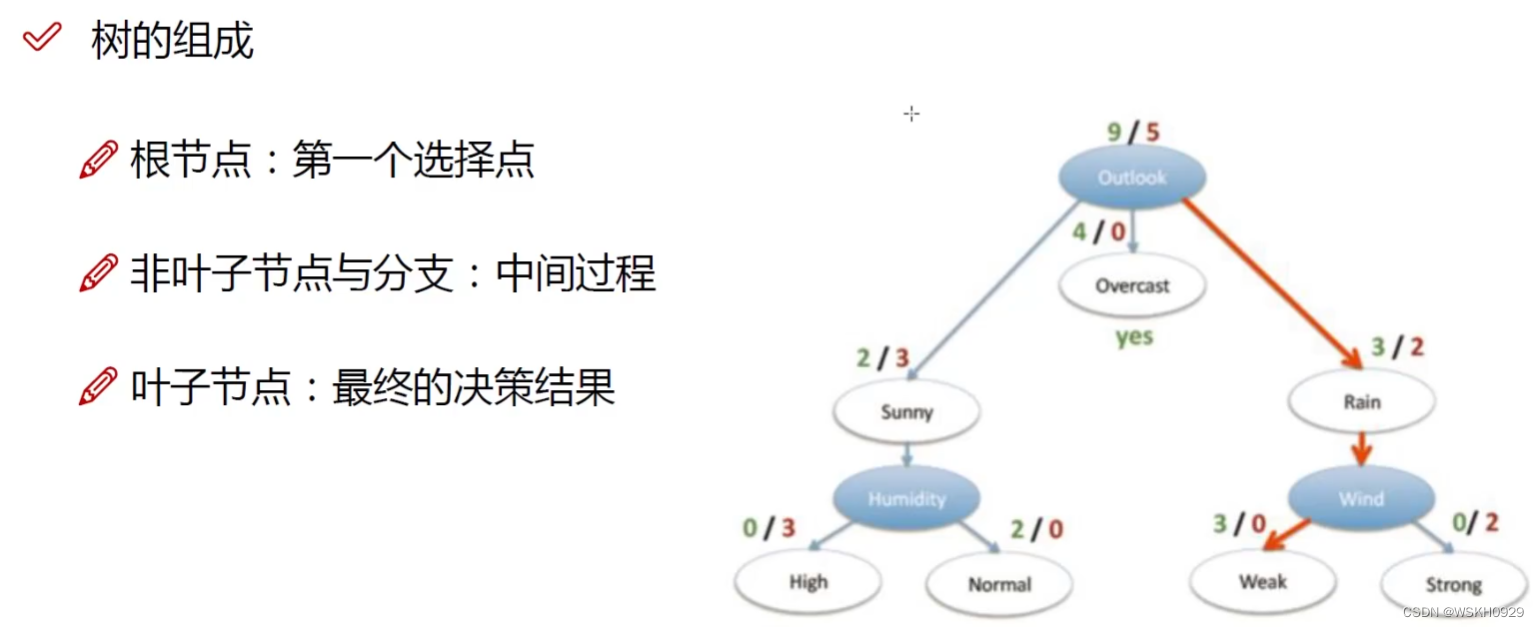
训练阶段(构造决策树):
测试阶段:根据训练出来的决策树从根节点往下走一遍就完事了
二、熵的作用
通过上面的讲解,我们肯定会疑惑,训练过程中根节点怎么选择用哪个特征进行判断呢?接下来的子节点又怎么选择呢?
答:选择分类效果最强的

但是,怎么评判一个特征的分类效果强还是不强呢?下面我们就介绍一个衡量标准:熵
简单理解:熵就是混乱程度
如:杂货铺卖的东西种类很多,可以说你去购买其中某个物品的熵很大
问:我们希望节点分支后数据类别的熵值大还是小呢?
答:当然希望熵值小。如果分支完熵值还是很大,那说明其还是很混乱,分支就没有什么作用了(我们最终目的是分类,每个决策树的叶子节点熵值都是很小的,都是纯纯的某一类)

三、信息增益
当概率P=0.5时,熵最大,最不确定
当P=0或1时,熵值最小,最确定
我们希望通过某特征判断后,熵值的下降越大越好,即不确定性减少的程度越大越好,而这个不确定性减少的程度就被成为信息增益。我们一般希望特征判断后信息增益越大越好。

四、决策树构造实例
4.1 问题描述
有四个特征(天气、温度、湿度、有无风),和一个标签(是否出去玩)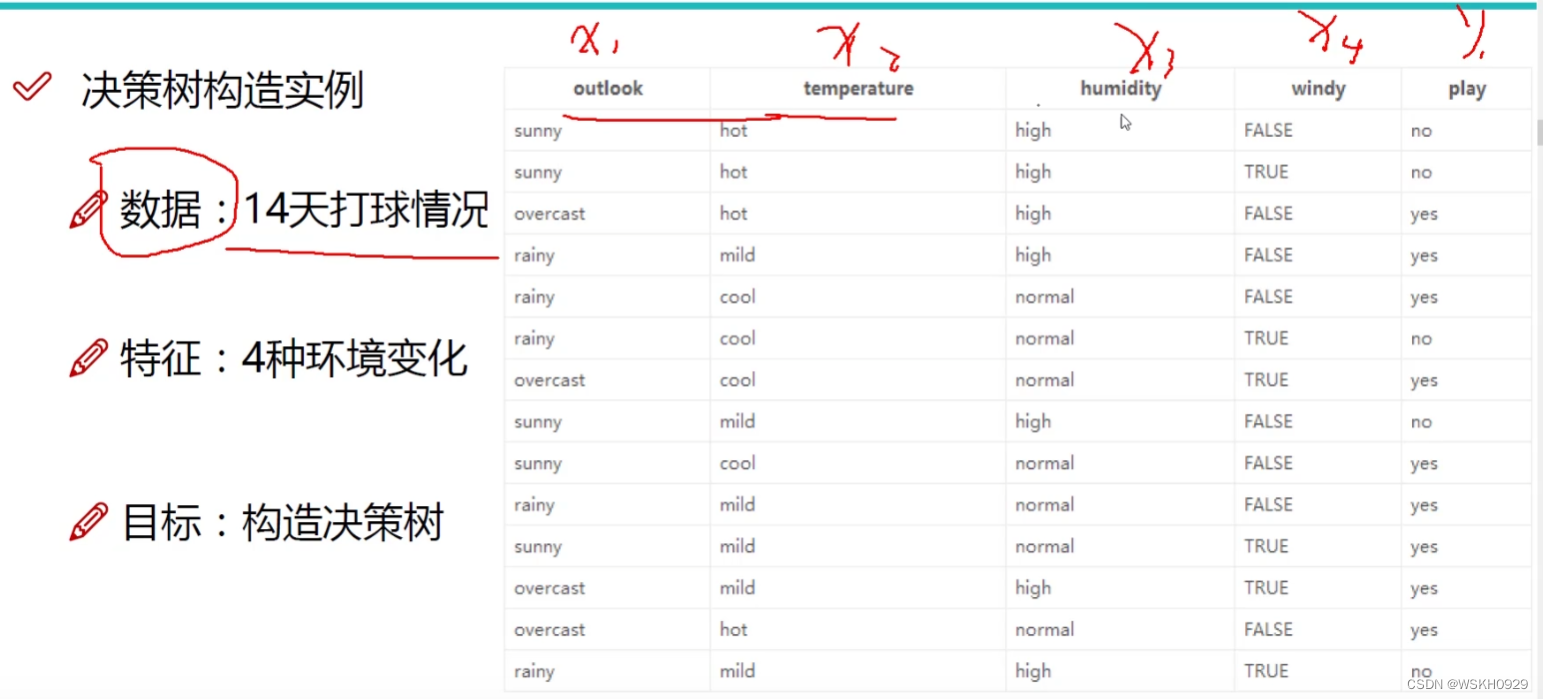
4.2 根节点构造
问题中有四个特征,故我们有4种构造根节点特征划分的方法。那我们怎么选择最好的特征划分呢?
前面说过了,看信息增益,选信息增益最大的特征划分构造根节点。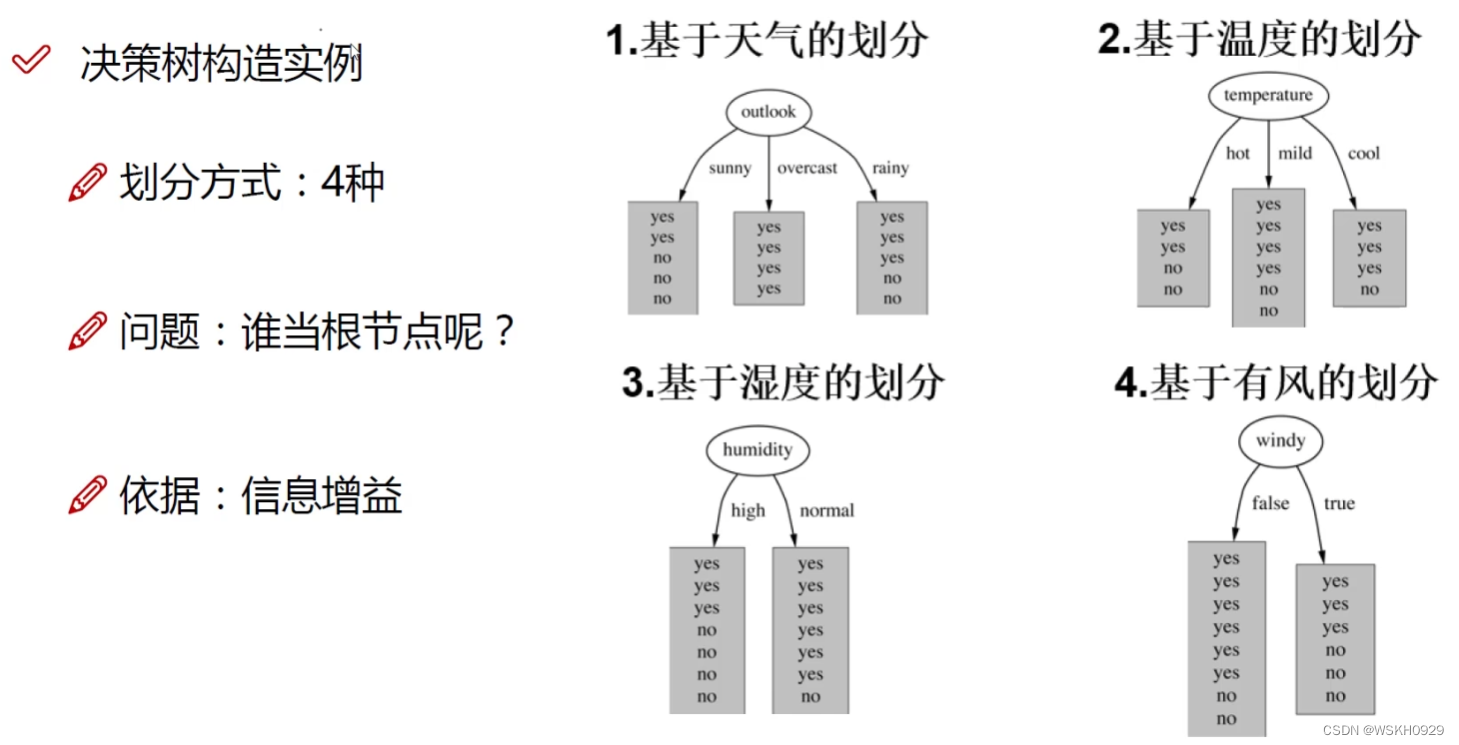
计算最开始没有进行特征划分时的数据的熵值:0.940

举例:基于天气的划分
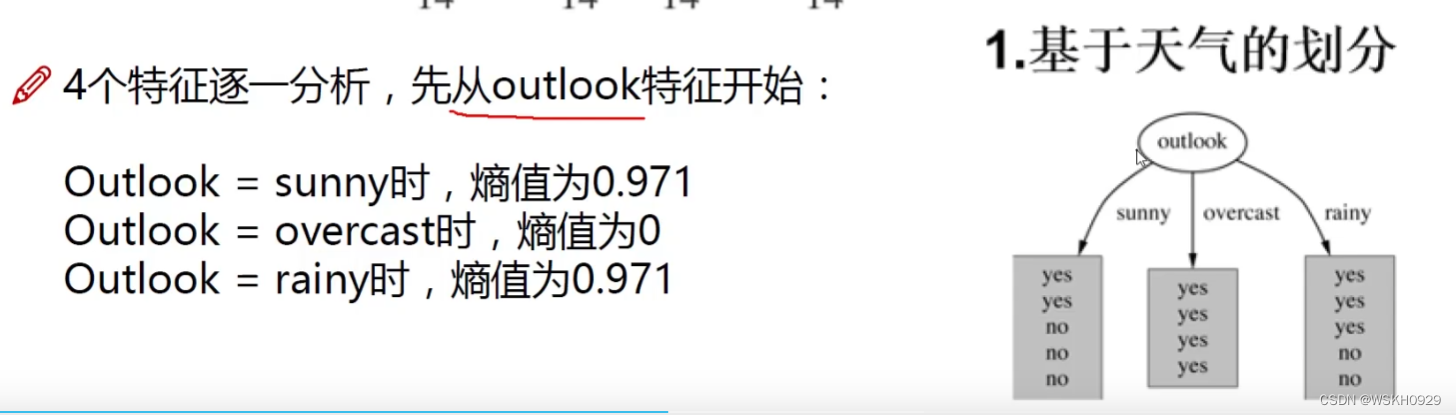
计算完每个种类的熵值之后,不能直接对其进行求和,而是进行加权的求和(取每个种类的概率作为权值)

从上图可以得出,信息增益最大的是outlook(基于天气的划分),所以根节点就以outlook进行特征划分,后面每一个节点的构造也是类似的步骤。
五、信息增益率和GINI系数
5.1 信息增益存在的问题
用信息增益来选取特征划分的方法,不适用与存在一个特征的可选值很多的情况(如将唯一编号id作为特征,每一个样本的id都不一样,导致用ID来作为根节点特征划分时,熵值直接下降为0,此时的信息增益为最大,但实际我们知道,用编号ID来作为根节点的特征划分是毫无意义的)

5.2 信息增益率
信息增益率= 信息增益 / 自身的熵值
例如计算编号的自身熵值,样本量为14,每一条样本的ID不同,故其概率 P = 1 14 \frac{1}{14} 141 ,根据熵值的计算公式可得,编号的自身熵值为:
编号的自身熵 = 14 ⋅ ( − 1 14 ⋅ log 2 ( 1 14 ) ) = 3.8074 编号的自身熵=14 \cdot\left(-\frac{1}{14} \cdot \log _2\left(\frac{1}{14}\right)\right)=3.8074 编号的自身熵=14⋅(−141⋅log2(141))=3.8074
再计算信息增益:
原始熵值 = − 5 14 log 2 ( 5 14 ) − 9 14 log 2 ( 9 14 ) = 0.9403 原始熵值=-\frac{5}{14} \log _2\left(\frac{5}{14}\right)-\frac{9}{14} \log _2\left(\frac{9}{14}\right)=0.9403 原始熵值=−145log2(145)−149log2(149)=0.9403
由于以ID进行特征划分后的熵值为0,故信息增益为:
信息增益 = 原始熵值 − 0 = 0.9403 信息增益=原始熵值 - 0 = 0.9403 信息增益=原始熵值−0=0.9403
综上,信息增益率为:
信息增益率 = 0.9403 3.8074 = 0.247 信息增益率=\frac{0.9403}{3.8074} = 0.247 信息增益率=3.80740.9403=0.247
同样的方法计算OutLook的信息增益率为0.2864,这样就避免了使用ID进行特征划分的情况。
显然利用信息增益率可以屏蔽掉类似ID类别过多的问题。
5.3 GINI系数
GINI系数的计算公式如下:
Gini ( p ) = ∑ k = 1 K p k ( 1 − p k ) = 1 − ∑ k = 1 K p k 2 \operatorname{Gini}(p)=\sum_{k=1}^K p_k\left(1-p_k\right)=1-\sum_{k=1}^K p_k^2 Gini(p)=k=1∑Kpk(1−pk)=1−k=1∑Kpk2
六、连续值特征划分
先对连续值特征进行升序排列以每两个相邻值的中间值进行特征划分,以下图为例,共有9种划分方式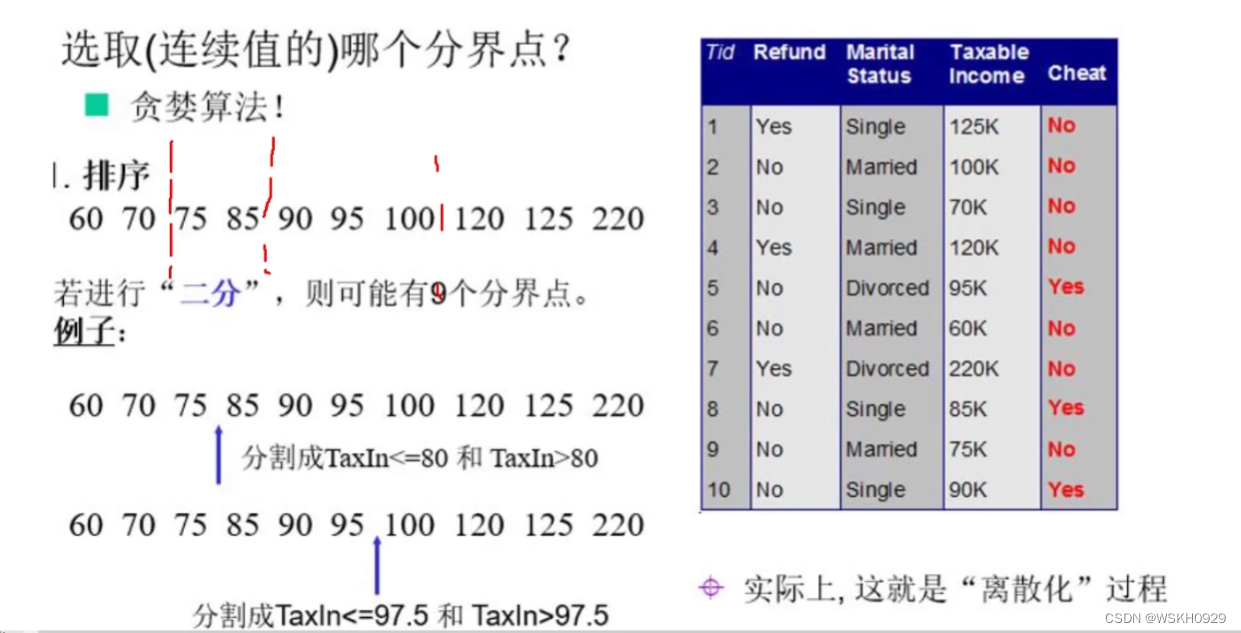
七、剪枝方法(预剪枝和后剪枝)
剪枝的目的:缓解过拟合

预剪枝:边建立决策树边剪枝(更实用)
限制树深度:相当于限制从根节点到叶子节点用来划分的特征个数限制叶子节点个数:设置决策树最末端的最大节点数(末端节点即叶子节点)限制叶子节点样本数:每个节点的最小样本数限制信息增益量:如果按照某特征进行划分后,信息增益量小于一个阈值,则不进行该特征划分后剪枝:建立完决策树后再进行剪枝操作
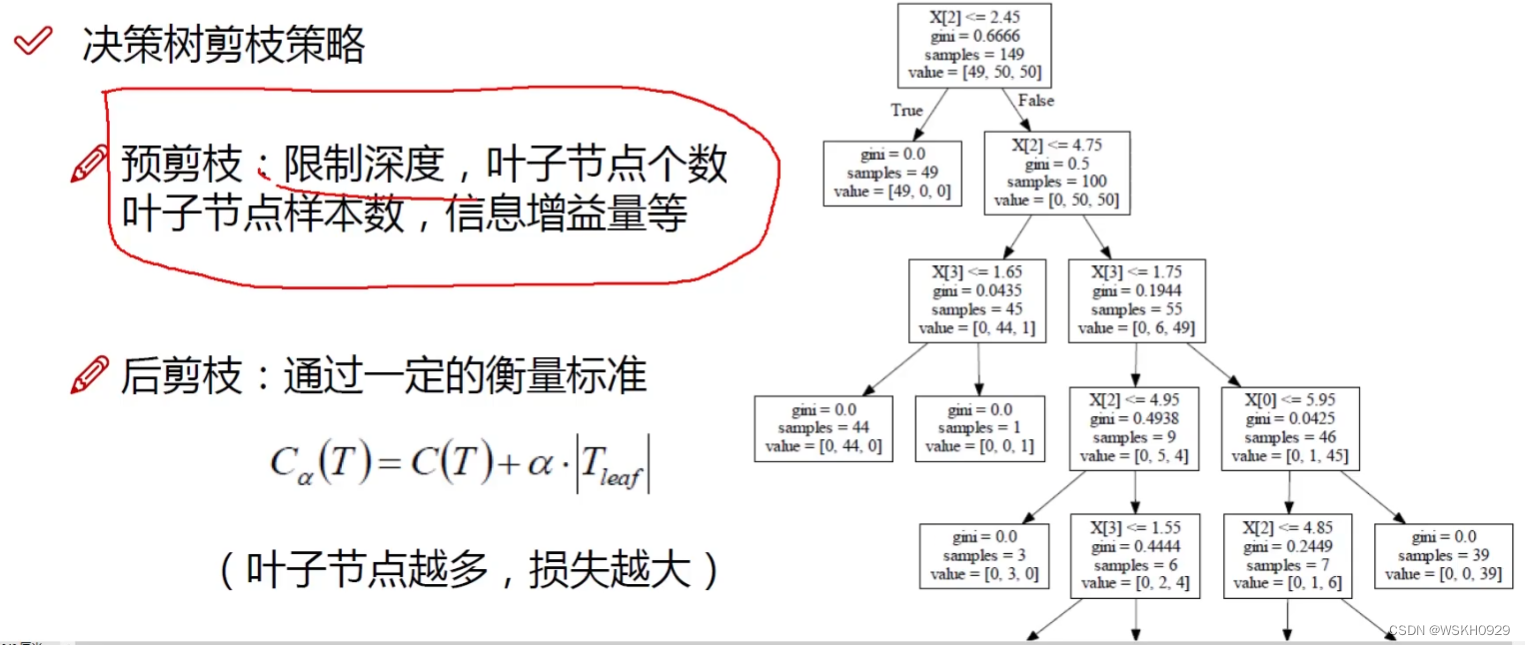
后剪枝的例子:
以下图的1处分支产生2处为例,按照公式计算1处的损失:
1 处的损失 = 0.4444 ∗ 6 + α 1处的损失=0.4444 * 6 + \alpha 1处的损失=0.4444∗6+α
2 处的损失 = 0 ∗ 3 + 0.4444 ∗ 3 + 2 α 2处的损失=0 * 3 + 0.4444 * 3 + 2\alpha 2处的损失=0∗3+0.4444∗3+2α
如果1处的损失小于2处的损失,则不应该进行分支,对1处进行后剪枝。
其中 α \alpha α 是个参数,我们可以对其进行设置,其越大,越难进行分支,就越不容易过拟合(但可能导致欠拟合)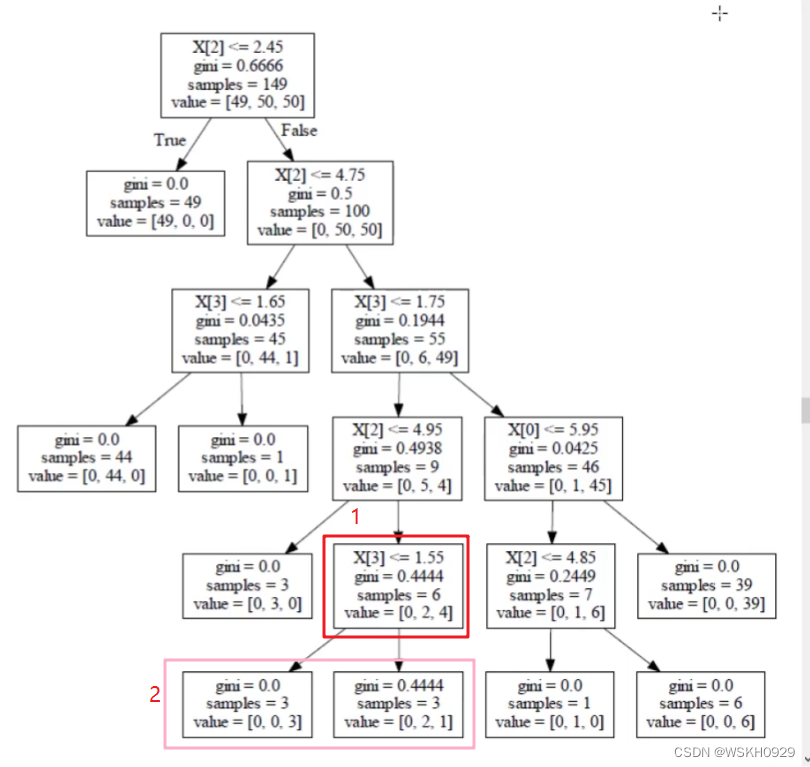
八、回归问题预测思路
如下所示,在回归问题中,右边叶子节点的输出等于该叶子节点中样本特征的平均值:
右边叶子节点的预测值 = 80 + 75 + 35 3 = 190 3 = 63.3333 右边叶子节点的预测值=\frac{80+75+35}{3}=\frac{190}{3}=63.3333 右边叶子节点的预测值=380+75+35=3190=63.3333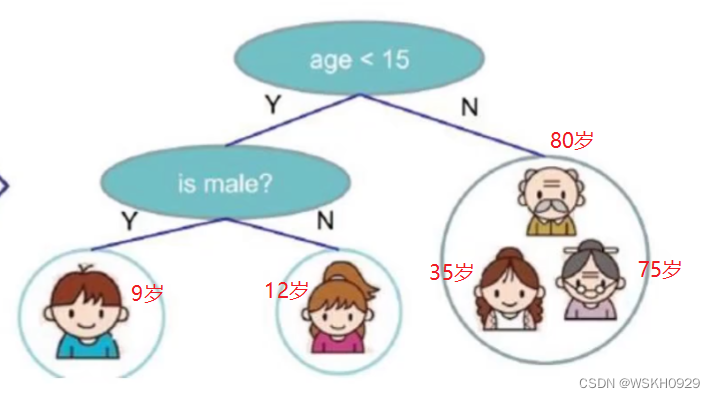
九、Python代码实现决策树
9.1 导入所需要的库
# 导入所需要的库import math9.2 构建数据集
# 创建数据def createDataSet(): # 数据 dataSet = [ [0, 0, 0, 0, 'no'], [0, 0, 0, 1, 'no'], [0, 1, 0, 1, 'yes'], [0, 1, 1, 0, 'yes'], [0, 0, 0, 0, 'no'], [1, 0, 0, 0, 'no'], [1, 0, 0, 1, 'no'], [1, 1, 1, 1, 'yes'], [1, 0, 1, 2, 'yes'], [1, 0, 1, 2, 'yes'], [2, 0, 1, 2, 'yes'], [2, 0, 1, 1, 'yes'], [2, 1, 0, 1, 'yes'], [2, 1, 0, 2, 'yes'], [2, 0, 0, 0, 'no'], ] # 列名 labels = ['F1-AGE', 'F2-WORK', 'F3-HOME', 'F4-LOAN'] return dataSet, labels9.3 函数编写
# 获取当前样本里最多的标签def getMaxLabelByDataSet(curLabelList): classCount = {} maxKey, maxValue = None, None for label in curLabelList: if label in classCount.keys(): classCount[label] += 1 if maxValuex < classCount[label]: maxKey, maxValue = label, classCount[label] else: classCount[label] = 1 if maxKey is None: maxKey, maxValue = label, 1 return maxKey# 计算熵值def calcEntropy(dataSet): # 1. 获取所有样本数 exampleNum = len(dataSet) # 2. 计算每个标签值的出现数量 labelCount = {} for featVec in dataSet: curLabel = featVec[-1] if curLabel in labelCount.keys(): labelCount[curLabel] += 1 else: labelCount[curLabel] = 1 # 3. 计算熵值(对每个类别求熵值求和) entropy = 0 for key, value in labelCount.items(): # 概率值 p = labelCount[key] / exampleNum # 当前标签的熵值计算并追加 curEntropy = -p * math.log(p, 2) entropy += curEntropy # 4. 返回 return entropy# 选择最好的特征进行分割,返回最好特征索引def chooseBestFeatureToSplit(dataSet): # 1. 计算特征个数 -1 是减去最后一列标签列 featureNum = len(dataSet[0]) - 1 # 2. 计算当前(未特征划分时)熵值 curEntropy = calcEntropy(dataSet) # 3. 找最好特征划分 bestInfoGain = 0 # 最大信息增益 bestFeatureIndex = -1 # 最好特征索引 for i in range(featureNum): # 拿到当前列特征 featList = [example[i] for example in dataSet] # 获取唯一值 uniqueVals = set(featList) # 新熵值 newEntropy = 0 # 计算分支(不同特征划分)的熵值 for val in uniqueVals: # 根据当前特征划分dataSet subDataSet = splitDataSet(dataSet, i, val) # 加权概率值 weight = len(subDataSet) / len(dataSet) # 计算熵值,追加到新熵值中 newEntropy += (calcEntropy(subDataSet) * weight) # 计算信息增益 infoGain = curEntropy - newEntropy # 更新最大信息增益 if bestInfoGain < infoGain: bestInfoGain = infoGain bestFeatureIndex = i # 4. 返回 return bestFeatureIndex# 根据当前选中的特征和唯一值去划分数据集def splitDataSet(dataSet, featureIndex, value): returnDataSet = [] for featVec in dataSet: if featVec[featureIndex] == value: # 将featureIndex那一列删除 deleteFeatVec = featVec[:featureIndex] deleteFeatVec.extend(featVec[featureIndex + 1:]) # 将删除后的样本追加到新的dataset中 returnDataSet.append(deleteFeatVec) return returnDataSet# 递归生成决策树节点def createTreeNode(dataSet, labels, featLabels): # 取出当前节点的样本的标签 -1 表示在最后一位 curLabelList = [example[-1] for example in dataSet] # -------------------- 停止条件 -------------------- # 1. 判断当前节点的样本的标签是不是已经全为1个值了,如果是则直接返回其唯一类别 if len(curLabelList) == curLabelList.count(curLabelList[0]): return curLabelList[0] # 2. 判断当前可划分的特征数是否为1,如果为1则直接返回当前样本里最多的标签 if len(labels) == 1: return getMaxLabelByDataSet(curLabelList) # -------------------- 下面是正常选择特征划分的步骤 -------------------- # 1. 选择最好的特征进行划分(返回值为索引) bestFeatIndex = chooseBestFeatureToSplit(dataSet) # 2. 利用索引获取真实值 bestFeatLabel = labels[bestFeatIndex] # 3. 将特征划分加入当前决策树 featLabels.append(bestFeatLabel) # 4. 构造当前节点 myTree = {bestFeatLabel: {}} # 5. 删除被选择的特征 del labels[bestFeatIndex] # 6. 获取当前最佳特征的那一列 featValues = [example[bestFeatIndex] for example in dataSet] # 7. 去重(获取唯一值) uniqueFeaValues = set(featValues) # 8. 对每个唯一值进行分支 for value in uniqueFeaValues: # 递归创建树 myTree[bestFeatLabel][value] = createTreeNode( splitDataSet(dataSet, bestFeatIndex, value), labels.copy(), featLabels.copy()) # 9. 返回 return myTree9.4 测试算法效果
# 测试一下!!!# 1. 获取数据集dataSet,labels = createDataSet()# 2. 构建决策树myDecisionTree = createTreeNode(dataSet,labels,[])# 3. 输出print(myDecisionTree)输出:
{'F3-HOME': {0: {'F2-WORK': {0: 'no', 1: 'yes'}}, 1: 'yes'}}十、SkLearn库实现决策树并可视化
10.1 Graphviz可视化库安装
进入下面网址
http://graphviz.gitlab.io/download/
点击右边菜单栏的Download按钮,然后选择一个版本进行下载(我选择了最新版的EXE格式的安装文件)
然后就是正常安装步骤即可
10.2 树模型的可视化展示
# 导入相关库from sklearn.datasets import load_irisfrom sklearn.tree import DecisionTreeClassifierfrom sklearn.tree import export_graphviz# 加载数据集iris = load_iris()# 获取特征x和标签yx = iris.data[:, 2:]y = iris.target# 创建决策树算法对象tree_clf = DecisionTreeClassifier(max_depth=2)# 构建决策树tree_clf.fit(x, y)# 导出.dot文件,为可视化做铺垫export_graphviz( tree_clf, out_file='iris_tree.dot', # 输出文件路径 feature_names=iris.feature_names[2:], class_names=iris.target_names, rounded=True, filled=True)获得.dot文件后,可以用下面的命令将其转化为png文件
dot -Tpng dot文件路径 -o 要输出的文件路径
例如:
dot -Tpng iris_tree.dot -o iris_tree.png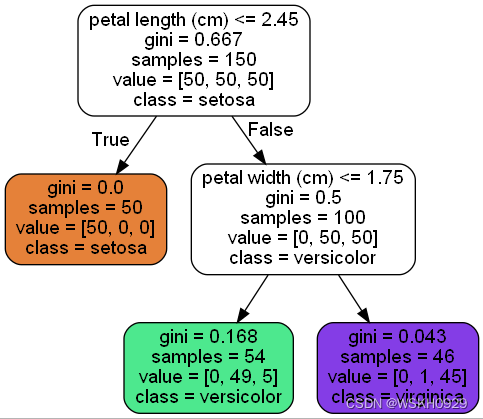
10.3 预剪枝参数及作用分析
10.3.1 预剪枝参数介绍
min_samples_split:节点在分割之前必须具有的最小样本数min_samples_.leaf:叶子节点必须具有的最小样本数max_leaf_nodes:叶子节点的最大数量max_features:在每个节点处评估用于拆分的最大特征数(除非特征非常多,否则不建议限制最大特征数)max_depth:树最大的深度10.3.2 预剪枝参数作用
预剪枝就是用来缓解过拟合的
下面让我们直观的感受一下预剪枝参数的作用:
首先,定义绘制决策边界的函数:
from matplotlib.colors import ListedColormapdef plot_decision_boundary(clf, X, y, axes=[0, 7.5, 0, 3], iris=True, legend=False, plot_training=True): x1s = np.linspace(axes[0], axes[1], 100) x2s = np.linspace(axes[2], axes[3], 100) x1, x2 = np.meshgrid(x1s, x2s) X_new = np.c_[x1.ravel(), x2.ravel()] y_pred = clf.predict(X_new).reshape(x1.shape) custom_cmap = ListedColormap(['#fafab0', '#9898ff', '#a0faa0']) plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap) if not iris: custom_cmap2 = ListedColormap(['#7d7d58', '#4c4c7f', '#507d50']) plt.contour(x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8) if plot_training: plt.plot(X[:, 0][y == 0], X[:, 1][y == 0], "yo", label="Iris-Setosa") plt.plot(X[:, 0][y == 1], X[:, 1][y == 1], "bs", label="Iris-Versicolor") plt.plot(X[:, 0][y == 2], X[:, 1][y == 2], "g^", label="Iris-Virginica") plt.axis(axes) if iris: plt.xlabel("Petal length", fontsize=14) plt.ylabel("Petal width", fontsize=14) else: plt.xlabel(r"$x_1$", fontsize=18) plt.ylabel(r"$x_2$", fontsize=18, rotation=0) if legend: plt.legend(loc="lower right", fontsize=14)然后是测试代码:
from sklearn.datasets import make_moonsimport matplotlib.pyplot as pltX, y = make_moons(n_samples=100, noise=0.25, random_state=53)tree_clf1 = DecisionTreeClassifier(random_state=42)tree_clf2 = DecisionTreeClassifier(min_samples_leaf=4, random_state=42)tree_clf1.fit(X, y)tree_clf2.fit(X, y)plt.figure(figsize=(12, 4))plt.subplot(121)plot_decision_boundary(tree_clf1, X, y, axes=[-1.5, 2.5, -1, 1.5], iris=False)plt.title('No Restrictions')plt.subplot(122)plot_decision_boundary(tree_clf2, X, y, axes=[-1.5, 2.5, -1, 1.5], iris=False)plt.title('min_samples_leaf = 4')结果:
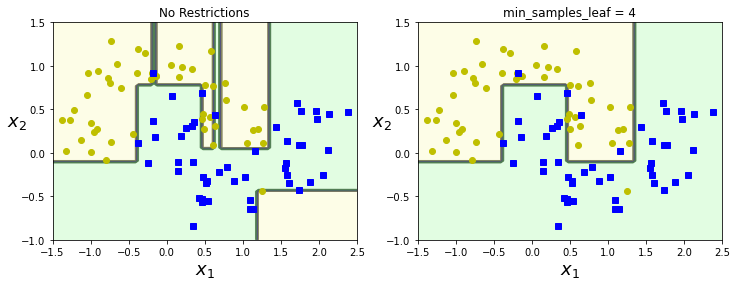
左边是没有增加预剪枝参数的决策边界,明显可以看出,它将一些离群点也考虑进去了,模型过为复杂,存在过拟合现象
而右边限制了 min_samples_leaf = 4 的决策树就没有存在明显的过拟合现象。
10.4 对数据的敏感性分析
先看左图,决策树很轻松的用一根垂直线将样本分成了两份,但如果我们对数据做一点小小的改动,将原本的数据进行90度旋转,如右图所示,决策边界就会复杂很多。
主要原因:决策树进行决策边界划分时只能沿着与坐标轴垂直的方向划分,所以对数据很敏感
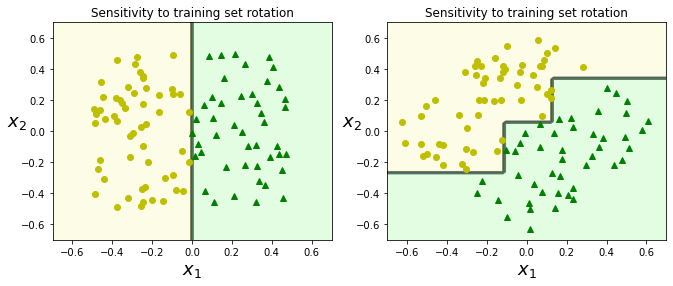
可视化代码(plot_decision_boundary函数见10.3.2节):
from sklearn.tree import DecisionTreeClassifierimport matplotlib.pyplot as pltimport numpy as npnp.random.seed(6)Xs = np.random.rand(100, 2) - 0.5ys = (Xs[:, 0] > 0).astype(np.int32)*2angle = np.pi / 4rotation_matrix = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]])Xsr = Xs.dot(rotation_matrix)tree_clf_s = DecisionTreeClassifier(random_state=42)tree_clf_s.fit(Xs, ys)tree_clf_sr = DecisionTreeClassifier(random_state=42)tree_clf_sr.fit(Xsr, ys)plt.figure(figsize=(11, 4))plt.subplot(121)plot_decision_boundary(tree_clf_s, Xs, ys, axes=[-0.7, 0.7, -0.7, 0.7], iris=False)plt.title('Sensitivity to training set rotation')plt.subplot(122)plot_decision_boundary(tree_clf_sr, Xsr, ys, axes=[-0.7, 0.7, -0.7, 0.7], iris=False)plt.title('Sensitivity to training set rotation')plt.show()10.5 回归任务
# 构建数据np.random.seed(42)m = 200X = np.random.rand(m,1)y = 4 * (X - 0.5)**2y = y + np.random.randn(m,1) / 10# 数据可视化plt.plot(X,y,'go')plt.show()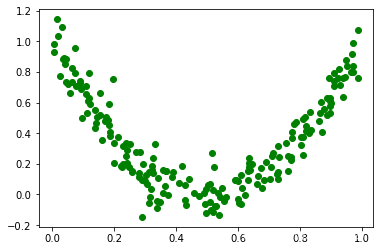
创建回归树对象并训练:
from sklearn.tree import DecisionTreeRegressor# 创建回归树tree_reg = DecisionTreeRegressor(max_depth=2)# 训练回归树tree_reg.fit(X, y)用10.2节中的可视化方法将树模型可视化:
可以发现,在回归树中,判断分支好坏的指标是MSE(均方差),分支后的子节点均方差越小越好,代表分支后,子节点的样本都比较接近,分类效果较好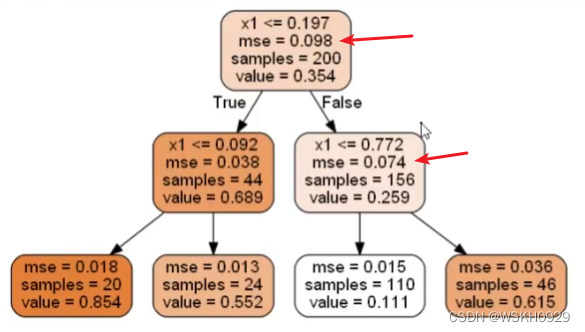
from sklearn.tree import DecisionTreeRegressortree_regl = DecisionTreeRegressor(random_state=42, max_depth=2)tree_reg2 = DecisionTreeRegressor(random_state=42, max_depth=3)tree_regl.fit(X, y)tree_reg2.fit(X, y)def plot_regression_predictions(tree_reg, X, y, axes=[0, 1, -0.2, 1], ylabel="$y$"): x1 = np.linspace(axes[0], axes[1], 500).reshape(-1, 1) y_pred = tree_reg.predict(x1) plt.axis(axes) plt.xlabel("$x_1$", fontsize=18) if ylabel: plt.ylabel(ylabel, fontsize=18, rotation=0) plt.plot(X, y, "b.") plt.plot(x1, y_pred, "r.-", linewidth=2, label=r"$\hat{y}$")plt.figure(figsize=(11, 4))plt.subplot(121)plot_regression_predictions(tree_regl, X, y)for split, style in ((0.1973, "k-"), (0.0917, "k-"), (0.7718, "k-")): plt.plot([split, split], [-0.2, 1], style, linewidth=2)plt.text(0.21, 0.65, "Depth=0", fontsize=15)plt.text(0.01, 0.2, "Depth=1", fontsize=13)plt.text(0.65, 0.8, "Depth=1", fontsize=13)plt.legend(loc="upper center", fontsize=18)plt.title("max_depth=2", fontsize=14)plt.subplot(122)plot_regression_predictions(tree_reg2,X,y,ylabel=None)for split,style in ((0.1973,"k-"),(0.0917,"k-"),(0.7718,"k-")): plt.plot([split,split],[-0.2,1],style,linewidth=2)for split in (0.0458,0.1298,0.2873,0.9040): plt.plot([split,split],[-0.2,1],"k:",linewidth=1)plt.text(0.3,0.5,"Depth=2",fontsize=13)plt.title("max_depth=3",fontsize=14)plt.show ()从下图可以看出,max_depth设置为3的模型较为复杂,max_depth设置为2的模型较为简单
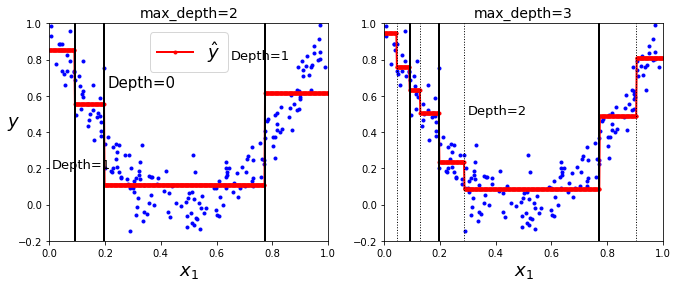
让我们不限制回归树模型看看它能多复杂
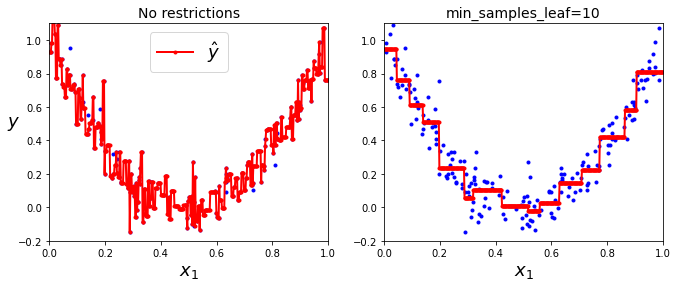
tree_reg1 = DecisionTreeRegressor(random_state=42)tree_reg2 = DecisionTreeRegressor(random_state=42, min_samples_leaf=10)tree_reg1.fit(X, y)tree_reg2.fit(X, y)x1 = np.linspace(0, 1, 500).reshape(-1, 1)y_pred1 = tree_reg1.predict(x1)y_pred2 = tree_reg2.predict(x1)plt.figure(figsize=(11, 4))plt.subplot(121)plt.plot(X, y, "b.")plt.plot(x1, y_pred1, "r.-", linewidth=2, label=r"$\hat{y}$")plt.axis([0, 1, -0.2, 1.1])plt.xlabel("$x_1$", fontsize=18)plt.ylabel("$y$", fontsize=18, rotation=0)plt.legend(loc="upper center", fontsize=18)plt.title("No restrictions", fontsize=14)plt.subplot(122)plt.plot(X,y,"b.")plt.plot(x1,y_pred2,"r.-",linewidth=2,label=r"$\hat{y}$")plt.axis([0,1,-0.2,1.1])plt.xlabel("$x_1$",fontsize=18)plt.title("min_samples_leaf=10".format (tree_reg2.min_samples_leaf),fontsize=14)plt.show()下图中可以看出,左边(不进行预剪枝)的回归树模型非常复杂,几乎拟合了所有点
右边限制了 min_samples_leaf=10 的回归树 就相对简单一些