前言
之前学习了 DDPM(DDPM原理与代码剖析)和 IDDPM(IDDPM原理和代码剖析), 这次又来学习另一种重要的扩散模型。它的采样速度比DDPM快很多(respacing),扩散过程不依赖马尔科夫链。
Denoising diffusion implicit models, ICLR 2021
理论
摘选paper一些重要思想。
Astract和Introduction部分
(1) 由于DDPM加噪基于马尔科夫链过程,那么在去噪过程过程也必须基于走这个过程,导致step数很多。
(2) DDIM的训练过程和DDPM一样,则可以利用起DDPM的权重,代码也可重用。而只要重新写一个sample的代码,就可以享受到采样step减少的好处。
(3) DDIM的采样过程是个确定的过程。
(4) 先有的概率模型主要有扩散的,也有分数的。
“Recent works on iterative generative models (Bengio et al., 2014), such as denoising diffusion probabilistic models (DDPM, Ho et al. (2020)) and noise conditional score networks (NCSN, Song & Ermon (2019))”
(5) 采样过程可以是郎之万,也可以是对逆扩散过程进行建模
“This generative Markov Chain process is either based on Langevin dynamics (Song & Ermon, 2019) or obtained by reversing a forward diffusion process that progressively turns an image into noise (Sohl-Dickstein et al., 2015).”
回顾DDPM
若没掌握过DDPM, 建议看下我之前的一篇博客 DDPM原理与代码剖析。
在ddim中, α t \alpha_t αt 相当于之前的 α ‾ t \overline{\alpha}_t αt
于是原来采样的公式变成了
q ( X 1 : T ∣ X 0 ) : = ∏ t = 0 T q ( X t ∣ X t − 1 ) q(X_{1:T}|X_0) := \prod_{t=0}^T q(X_t|X_{t-1}) q(X1:T∣X0):=∏t=0Tq(Xt∣Xt−1), where q ( X t ∣ X t − 1 ) : = N ( α t α t − 1 X t − 1 , ( 1 − α t α t − 1 ) I ) q(X_t|X_{t-1}) := N(\sqrt{\frac{\alpha_t}{\alpha_{t-1}}}X_{t-1}, (1-\frac{\alpha_t}{\alpha_{t-1}})I) q(Xt∣Xt−1):=N(αt−1αt Xt−1,(1−αt−1αt)I)
A special property of the forward process is that
q ( X t ∣ X 0 ) : = N ( X t ; α t X 0 , ( 1 − α t ) I ) q(X_t|X_0) := N(X_t; \sqrt{\alpha_t}X_0, (1-\alpha_t)I) q(Xt∣X0):=N(Xt;αt X0,(1−αt)I)
X t = α t X 0 + 1 − α t ϵ X_t = \sqrt{\alpha_t}X_0 + \sqrt{1-\alpha_t}\epsilon Xt=αt X0+1−αt ϵ
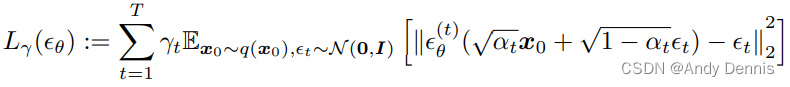
Variational Inference for Non-markovian Forward Processes
(1) DDPM的 L s i m p l e L_{simple} Lsimple 只依赖边缘分布,而不直接依赖联合分布。
Our key observation is that the DDPM objective in the form of L γ L_γ Lγ only depends on the marginals q ( X t ∣ X 0 ) q(X_t|X_0) q(Xt∣X0), but not directly on the joint q ( X 1 : T ∣ X 0 ) q(X_{1:T} |X_{0}) q(X1:T∣X0).
这是设计出非马尔科夫加噪过程的理论基础。
by the way, DDIM最后设计出来的 q ( X t ∣ X 0 ) q(X_t|X_0) q(Xt∣X0) 还和DDPM的形式一样,于是他们可以共用同一套目标函数。
(2) 在推导出 L s i m p l e L_{simple} Lsimple 过程中,我们没有使用到 q ( X 1 : T ∣ X 0 ) q(X_{1:T} |X_{0}) q(X1:T∣X0) 的具体形式,只是基于贝叶斯公式和 q ( X t ∣ X t − 1 , X 0 ) q(X_t|X_{t-1}, X_0) q(Xt∣Xt−1,X0), q ( X t ∣ X 0 ) q(X_t|X_0) q(Xt∣X0) 的表达式。
噪音项是来自 q ( X t ∣ X 0 ) q(X_t|X_0) q(Xt∣X0) 的采样,因此,ddpm的的目标函数其实只由 q ( X t ∣ X 0 ) q(X_t|X_0) q(Xt∣X0) 表达式决定。
换句话说,只要让 q ( X t ∣ X 0 ) q(X_t|X_0) q(Xt∣X0) 满足高斯分布, 就可以用DDPM预测噪声的方式来训练扩散模型。
(3) 在DDPM中,假设 q ( X t ∣ X t − 1 , X 0 ) = q ( X t ∣ X t − 1 ) q(X_t|X_{t-1}, X_0) = q(X_t|X_{t-1}) q(Xt∣Xt−1,X0)=q(Xt∣Xt−1), 也就意味着它要满足马尔科夫链性质。那么如果我们可以把 q ( X t ∣ X t − 1 , X 0 ) q(X_t|X_{t-1}, X_0) q(Xt∣Xt−1,X0) 推广为更一般的形式, 并且保证 q ( X t ∣ X 0 ) q(X_t|X_0) q(Xt∣X0) 形式不变,就可以用更少的step采样,同时复用DDPM的训练方式和模型权重。

上述过程只说明 T 时刻满足与DDPM同样的 q ( X T ∣ X 0 ) q(X_T|X_0) q(XT∣X0), 但不能说明所有的 t 时刻,接下来就要证明:
前置知识:(截图来自: 64、扩散模型加速采样算法DDIM论文精讲与PyTorch源码逐行解读 1:06:20)
根据以上前置知识和数学归纳法,可以有以下证明过程(原论文附录 part B)

优化函数:

当 σ t = 0 \sigma_t = 0 σt=0 时,就是一个确定性的生成过程了, 这时候就是DDIM了。
respacing
respacing是一种加速采样的技巧。
训练可以是一个长序列,而采样可以只在子序列上进行。
效果比较
代码
案例主要基于这份OpenAI官方代码 openai/improved-diffusion 。
关于主要代码已经在上一篇博文 IDDPM原理和代码剖析 交代了, 这里只要关注一下与 DDIM 相关的代码。
ddim_sample
Sample x_{t-1} from the model using DDIM. Same usage as p_sample().
out 是 { “mean”: model_mean, “variance”: model_variance,
“log_variance”: model_log_variance, “pred_xstart”: pred_xstart} 组成的字典
out = self.p_mean_variance( model, x, t, clip_denoised=clip_denoised, denoised_fn=denoised_fn, model_kwargs=model_kwargs, )推出噪声
eps = self._predict_eps_from_xstart(x, t, out["pred_xstart"])先取出 α ‾ t \overline{\alpha}_{t} αt 和 α ‾ t − 1 \overline{\alpha}_{t-1} αt−1
alpha_bar = _extract_into_tensor(self.alphas_cumprod, t, x.shape)alpha_bar_prev = _extract_into_tensor(self.alphas_cumprod_prev, t, x.shape)然后根据公式 σ = η ( 1 − α τ i − 1 ) / ( 1 − α τ i ) 1 − α τ i / α τ i − 1 \sigma = \eta \sqrt{(1-\alpha_{\tau_{i-1}})/(1-\alpha_{\tau_{i}})} \sqrt{1-\alpha_{\tau_{i}}/\alpha_{\tau_{i-1}}} σ=η(1−ατi−1)/(1−ατi) 1−ατi/ατi−1 算出 σ \sigma σ
sigma = ( eta * th.sqrt((1 - alpha_bar_prev) / (1 - alpha_bar)) * th.sqrt(1 - alpha_bar / alpha_bar_prev) )
mean_pred = ( out["pred_xstart"] * th.sqrt(alpha_bar_prev) + th.sqrt(1 - alpha_bar_prev - sigma ** 2) * eps )得到 X t − 1 X_{t-1} Xt−1 时刻的采样结果
nonzero_mask = ( (t != 0).float().view(-1, *([1] * (len(x.shape) - 1))) ) # no noise when t == 0sample = mean_pred + nonzero_mask * sigma * noise最后返回 X t − 1 X_{t-1} Xt−1 的采样结果和预测的 X 0 X_{0} X0
ddim_sample_loop_progressive函数会迭代调用这个函数。
respace.py
space_timesteps
该函数返回采样的子序列
For example, if there’s 300 timesteps and the section counts are [10,15,20],then the first 100 timesteps are strided to be 10 timesteps, the second 100 are strided to be 15 timesteps, and the final 100 are strided to be 20.
def space_timesteps(num_timesteps, section_counts): if isinstance(section_counts, str): if section_counts.startswith("ddim"): desired_count = int(section_counts[len("ddim") :]) for i in range(1, num_timesteps): if len(range(0, num_timesteps, i)) == desired_count: return set(range(0, num_timesteps, i)) raise ValueError( f"cannot create exactly {num_timesteps} steps with an integer stride" ) section_counts = [int(x) for x in section_counts.split(",")] size_per = num_timesteps // len(section_counts) extra = num_timesteps % len(section_counts) start_idx = 0 all_steps = [] for i, section_count in enumerate(section_counts): size = size_per + (1 if i < extra else 0) if size < section_count: raise ValueError( f"cannot divide section of {size} steps into {section_count}" ) if section_count <= 1: frac_stride = 1 else: frac_stride = (size - 1) / (section_count - 1) cur_idx = 0.0 taken_steps = [] for _ in range(section_count): taken_steps.append(start_idx + round(cur_idx)) cur_idx += frac_stride all_steps += taken_steps start_idx += size return set(all_steps)SpacedDiffusion
respace.py文件中的一个类,继承自GaussianDiffusion, 它会覆盖父类的一些函数。 “A diffusion process which can skip steps in a base diffusion process.”
init
当前子序列 和 原始序列步长
self.use_timesteps = set(use_timesteps)self.original_num_steps = len(kwargs["betas"])计算子序列的加噪方案new_betas, 同时记录子序列相对于原序列的下标,方便后续反推
new_betas = []for i, alpha_cumprod in enumerate(base_diffusion.alphas_cumprod): if i in self.use_timesteps: new_betas.append(1 - alpha_cumprod / last_alpha_cumprod) last_alpha_cumprod = alpha_cumprod self.timestep_map.append(i)更新一下betas
kwargs["betas"] = np.array(new_betas)super().__init__(**kwargs)该类的 p_mean_variance 函数 和 training_losses 函数都经过了一个包裹函数
def p_mean_variance( self, model, *args, **kwargs ): # pylint: disable=signature-differs return super().p_mean_variance(self._wrap_model(model), *args, **kwargs)def training_losses( self, model, *args, **kwargs ): # pylint: disable=signature-differs return super().training_losses(self._wrap_model(model), *args, **kwargs)def _wrap_model(self, model): if isinstance(model, _WrappedModel): return model return _WrappedModel( model, self.timestep_map, self.rescale_timesteps, self.original_num_steps )_WrappedModel
timestep_map是子序列相对于原序列的下标
class _WrappedModel: def __init__(self, model, timestep_map, rescale_timesteps, original_num_steps): self.model = model self.timestep_map = timestep_map self.rescale_timesteps = rescale_timesteps self.original_num_steps = original_num_steps def __call__(self, x, ts, **kwargs): map_tensor = th.tensor(self.timestep_map, device=ts.device, dtype=ts.dtype) new_ts = map_tensor[ts] if self.rescale_timesteps: new_ts = new_ts.float() * (1000.0 / self.original_num_steps) return self.model(x, new_ts, **kwargs)