?博客主页: 小羊失眠啦.
?系列专栏:《C语言》 《数据结构》 《C++》 《Linux》 《Cpolar》
❤️感谢大家点赞?收藏⭐评论✍️

文章目录
试题A:握手问题问题描述思路 试题B:小球反弹问题描述思路 试题C:好数问题描述思路 试题D:R格式问题描述思路 试题E:宝石组合问题描述思路
试题A:握手问题
问题描述
小蓝组织了一场算法交流会议,总共有 50 人参加了本次会议。在会议上, 大家进行了握手交流。按照惯例他们每个人都要与除自己以外的其他所有人进 行一次握手(且仅有一次)。但有 7 个人,这 7 人彼此之间没有进行握手(但 这 7 人与除这 7 人以外的所有人进行了握手)。请问这些人之间一共进行了多 少次握手?
注意 A 和 B 握手的同时也意味着 B 和 A 握手了,所以算作是一次握手。
思路
总共有50人参加了会议,其中7个人之间没有握手,但他们与其他43个人都握过手,握手次数为7*43=301次。
另外43个人之间握手的次数可以通过组合公式计算:C(43,2)=903次。
所以,这些人之间一共进行了 301+903=1204次握手。
因此,答案是:1204次。
#include <iostream>#include <cmath> using namespace std;int countHandshakes(int total, int group) { int groupHandshakes = group * (total - group); int otherHandshakes = (total - group) * (total - group - 1) / 2; return groupHandshakes + otherHandshakes;}int main() { int total = 50; int group = 7; int numHandshakes = countHandshakes(total, group); cout << "这些人之间一共进行了 " << numHandshakes << " 次握手" << endl; return 0;}试题B:小球反弹
问题描述
有一长方形,长为 343720 单位长度,宽为 233333 单位长度。在其内部左 上角顶点有一小球(无视其体积),其初速度如图所示且保持运动速率不变,分 解到长宽两个方向上的速率之比为 dx : dy = 15 : 17。小球碰到长方形的边框时 会发生反弹,每次反弹的入射角与反射角相等,因此小球会改变方向且保持速 率不变(如果小球刚好射向角落,则按入射方向原路返回)。从小球出发到其第 一次回到左上角顶点这段时间里,小球运动的路程为多少单位长度?答案四舍 五入保留两位小数。
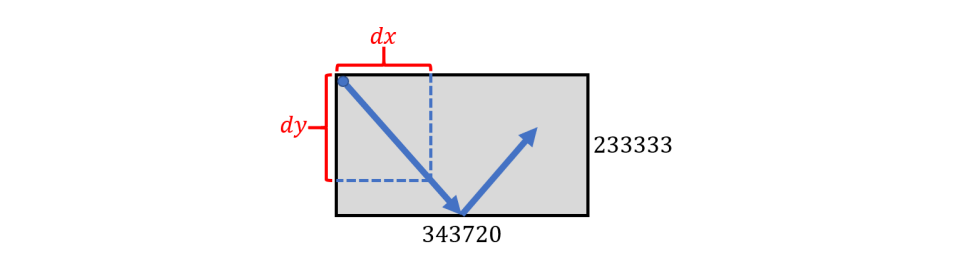
思路
为了计算小球运动的路程,我们需要模拟小球在长方形内的反弹过程,直到它再次回到左上角顶点。由于小球在长宽方向上的速率之比是恒定的(dx : dy = 15 : 17),我们可以将问题分解为两个独立的一维问题,分别处理小球在长和宽方向上的运动。
首先,我们需要确定小球在碰到哪一边之前会先碰到另一边。这可以通过比较小球在两个方向上到达边界所需的时间来实现。一旦小球碰到边界,它就会以相同的角度反弹。我们可以记录每次反弹的位置和方向,直到小球再次回到起始点。
#include <iostream> #include <cmath> #include <iomanip> using namespace std;struct Point { Point(double x = 0, double y = 0) : x(x) , y(y) {} double x, y;};struct Velocity { Velocity(double dx = 0, double dy = 0) : dx(dx) , dy(dy) {} double dx, dy;};double calculateDistance(double length, double width, const Velocity& v) { double totalDistance = 0; Point position(0, 0); // 初始位置为左上角顶点 Velocity currentVelocity = v; while (true) { // 计算小球在长和宽方向上分别需要多长时间到达边界 double timeToHitX = (length - position.x) / currentVelocity.dx; double timeToHitY = (width - position.y) / currentVelocity.dy; // 根据时间决定小球先碰到哪一边 if (timeToHitX < timeToHitY) { // 碰到长方形的右边 totalDistance += position.x + currentVelocity.dx * timeToHitX; currentVelocity.dx = -currentVelocity.dx; // 反弹 position.x = length - currentVelocity.dx * timeToHitX; } else { // 碰到长方形的下边 totalDistance += position.y + currentVelocity.dy * timeToHitY; currentVelocity.dy = -currentVelocity.dy; // 反弹 position.y = width - currentVelocity.dy * timeToHitY; } // 检查是否回到起始点 if (position.x == 0 && position.y == 0) { break; // 如果回到起始点,退出循环 } } return totalDistance;}int main() { double length = 343720; // 长方形长 double width = 233333; // 长方形宽 Velocity v(15, 17); // 小球的速率比 // 计算小球运动的总路程 double totalDistance = calculateDistance(length, width, v); // 输出结果,保留两位小数 cout << fixed << setprecision(2) << totalDistance << endl; return 0;}试题C:好数
问题描述
一个整数如果按从低位到高位的顺序,奇数位(个位、百位、万位 · · · )上 的数字是奇数,偶数位(十位、千位、十万位 · · · )上的数字是偶数,我们就称 之为“好数”。
给定一个正整数 N,请计算从 1 到 N 一共有多少个好数。
输入格式
一个整数 N。
输出格式
一个整数代表答案。
样例输入
24
2024
样例输出
7
150
样例说明
对于第一个样例,24 以内的好数有 1、3、5、7、9、21、23,一共 7 个。
评测用例规模与约定
对于 10% 的评测用例,1 ≤ N ≤ 100。
对于 100% 的评测用例,1 ≤ N ≤ 107。
思路
遍历从1到N的所有整数,判断每个整数是否满足好数的条件,如果满足则计数器加1。
条件:定位一个flag在奇数位上为1,在偶数位上为-1,判断奇数位上是否为奇数且flag是否为1或者偶数位上是否为偶数且flag是否为-1
#include <iostream>using namespace std;bool isGoodNumber(int num) { int flag = 1; while (num ) { int current = num % 10; if (!((flag == 1 && current % 2) || (flag == -1 && current % 2 == 0))) return false; num /= 10; flag *= -1; } return true;}int countGoodNumbers(int N) { int count = 0; for (int i = 1; i <= N; i++) { if (isGoodNumber(i)) count++; } return count;}int main() { int N = 0; cin >> N; cout << countGoodNumbers(N) << endl; return 0;}试题D:R格式
问题描述
小蓝最近在研究一种浮点数的表示方法:R 格式。对于一个大于 0 的浮点 数 d,可以用 R 格式的整数来表示。给定一个转换参数 n,将浮点数转换为 R 格式整数的做法是:
将浮点数乘以 2的n次方 ;四舍五入到最接近的整数。输入格式
一行输入一个整数 n 和一个浮点数 d,分别表示转换参数,和待转换的浮 点数。
输出格式
输出一行表示答案:d 用 R 格式表示出来的值。
样例输入
2 3.14
样例输出
13
样例说明
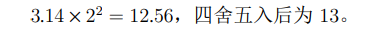
评测用例规模与约定
对于 50% 的评测用例:1 ≤ n ≤ 10,1 ≤ 将 d 视为字符串时的长度 ≤ 15。
对于 100% 的评测用例:1 ≤ n ≤ 1000,1 ≤ 将 d 视为字符串时的长度 ≤ 1024;
保证 d 是小数,即包含小数点。
思路
首先,我们需要定义一个函数convertToRFormat,该函数接受一个浮点数d和一个整数n作为参数。在函数中,我们首先计算转换因子factor,即2的n次方。然后,我们将浮点数d乘以转换因子factor,得到一个新的浮点数。最后,我们使用四舍五入函数round将新的浮点数四舍五入到最接近的整数,并将结果返回。 #include <iostream>#include <cmath>using namespace std;long long convertToRFormat(double d, int n) { double factor = pow(2, n); long long result = round(d * factor); return result;}int main() { double d = 0.0; int n = 0; cin >> n >> d; long long rFormat = convertToRFormat(d, n); cout << rFormat << endl; return 0;}试题E:宝石组合
问题描述
在一个神秘的森林里,住着一个小精灵名叫小蓝。有一天,他偶然发现了 一个隐藏在树洞里的宝藏,里面装满了闪烁着美丽光芒的宝石。这些宝石都有 着不同的颜色和形状,但最引人注目的是它们各自独特的 “闪亮度” 属性。每颗 宝石都有一个与生俱来的特殊能力,可以发出不同强度的闪光。小蓝共找到了 N 枚宝石,第 i 枚宝石的 “闪亮度” 属性值为 Hi,小蓝将会从这 N 枚宝石中选 出三枚进行组合,组合之后的精美程度 S 可以用以下公式来衡量:
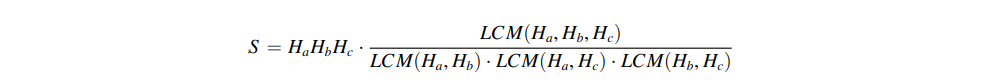
其中 LCM 表示的是最小公倍数函数。
小蓝想要使得三枚宝石组合后的精美程度 S 尽可能的高,请你帮他找出精 美程度最高的方案。如果存在多个方案 S 值相同,优先选择按照 H 值升序排列 后字典序最小的方案。
输入格式
第一行包含一个整数 N 表示宝石个数。
第二行包含 N 个整数表示 N 个宝石的 “闪亮度”。
输出格式
输出一行包含三个整数表示满足条件的三枚宝石的 “闪亮度”。
样例输入
5
1 2 3 4 9
样例输出
1 2 3
评测用例规模与约定
对于 30% 的评测用例:3 ≤ N ≤ 100,1 ≤ Hi ≤ 1000。
对于 60% 的评测用例:3 ≤ N ≤ 2000。
对于 100% 的评测用例:3 ≤ N ≤ 105,1 ≤ Hi ≤ 105。
思路
我们需要找到三枚宝石的组合,使得他们的最小公倍数与各自“闪亮度”属性值的乘积之和最大。此外,如果有多个最大精美程度的方案,我们还需要根据H值的升序排列选择字典序最小的方案。
首先,我们需要实现计算两个数的最小公倍数(LCM)的函数,通常LCM可以通过两数乘积除以它们的最大公约数(GCD)来得到。然后,我们需要遍历所有可能的宝石组合,计算每个组合的精美程度,并跟踪最大的S值以及对应的宝石组合。
#include <iostream> #include <vector> #include <algorithm> using namespace std;// 计算最大公约数 float gcd(int a, int b) { if (b == 0) return a; return gcd(b, a % b);}// 计算最小公倍数 float lcm(int a, int b) { return a * b / gcd(a, b);}// 定义一个宝石的结构体 struct Gem { int H; // 闪亮度 int index; // 宝石的索引,用于记录宝石的原始顺序 };// 自定义比较函数,用于按H值升序排序 bool compareGems(const Gem& a, const Gem& b) { if (a.H == b.H) return a.index < b.index; // 如果H值相同,按索引升序排列 return a.H < b.H;}// 查找最大精美程度的宝石组合 vector<int> findMaxBeautyCombination(const vector<int>& gems) { int N = gems.size(); vector<Gem> gemVec(N); for (int i = 0; i < N; ++i) { gemVec[i].H = gems[i]; gemVec[i].index = i; } // 按H值升序排序 sort(gemVec.begin(), gemVec.end(), compareGems); float maxBeauty = 0; vector<int> bestCombination; // 遍历所有可能的宝石组合 for (int i = 0; i < N - 2; ++i) { for (int j = i + 1; j < N - 1; ++j) { for (int k = j + 1; k < N; ++k) { float beauty = (gemVec[i].H * 100 + gemVec[j].H * 10 + gemVec[k].H) * (lcm(lcm(gemVec[i].H, gemVec[j].H), gemVec[k].H) / (lcm(gemVec[i].H, gemVec[j].H) * lcm(gemVec[j].H, gemVec[k].H) * lcm(gemVec[i].H, gemVec[k].H))); if (beauty > maxBeauty) { maxBeauty = beauty; bestCombination = { gemVec[i].H, gemVec[j].H, gemVec[k].H }; } } } } return bestCombination;}int main() { int N; cin >> N; // 输入宝石数量 vector<int> gems(N); for (int i = 0; i < N; ++i) cin >> gems[i]; // 输入每颗宝石的闪亮度 // 查找最大精美程度的宝石组合 vector<int> result = findMaxBeautyCombination(gems); // 输出结果 for (int H : result) cout << H << " "; cout << endl; return 0;}