前言

PCA多用于对数据特征集进行降维，也方便对数据集进行可视化操作，说白了最后进行结果展示那么多特征向量要一起表示的话肯定很难展示，超过三维的数据就很难展示了。而PCA可对特征集进行简化，通俗的来讲也就是合并好理解。PCA应用的范围很广因此很有必要要学习，原理肯定还是数学证明，在特征工程上经常使用。希望读者看完能够提出错误或者看法，博主会长期维护博客做及时更新。纯分享，希望大家喜欢。

强烈推荐大家看看这篇Python机器学习笔记：主成分分析（PCA）算法，写的很详细很好。

一、为什么需要PCA？（为什么要降维）

在各个领域进行数据收集或是数据采样时往往都是存在多个指标或是特征用来表示某一现象或是用来作评估好坏。但是庞大的数据量难以展示，对多维数据分析的难度很大。更重要的是在多数情况下，许多变量之间可能存在相关性，从而增加了问题分析的复杂性，同时对分析带来不便。如果分别对每个指标进行分析，分析往往是孤立的，而不是综合的。盲目减少指标会损失很多信息，容易产生错误的结论。

我们常常用二维模型来进行结果展示，通常进行展示的数据都是二维数据，但是想象一下对于四维以及四维以上的数据我们该如何进行展示？

例如我们要对地铁拥堵情况进行评估和展示，对于评估地铁拥堵情况，我们将采用

日期

天气情况

湿度

风级

降水量

体感温度

节假日波动系数

突发事件

客流量

这九个指标进行预测地铁拥堵情况。我们通常在一张坐标轴上进行效果展示从而进行分析，但在对这些多维数据进行展示的话我们寻常的展示效果图肯定展示不出来。数据往往拥有超出显示能力的更多特征。数据显示并非大规模特征下的唯一难题，对数据进行简化还有如下一系列的原因：

使得数据集更容易使用；
降低很多算法的计算开销；
去除噪声；
使得结果容易理解；

在已标注与未标注的数据上都有降维技术。这里我们将主要关注未标注数据上的降维技术，该技术同时也可以应用于已标注的数据。

而在数据特征工程降维技术中，PCA的应用目前最为广泛。

二、PCA简介

主成分分析法（PCA）是设法将原来变量重新组合成一组新的相互无关的几个综合变量，同时根据实际需要从中可以取出几个较少的总和变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析，也是数学上处理降维的一种方法。主成分分析是设法将原来众多具有一定相关性（比如P个指标），重新组合成一组新的互相无关的综合指标来代替原来的指标。通常数学上的处理就是将原来P个指标作线性组合，作为新的综合指标。

在数学上更简单的理解我们可以把它想象为对很多个坐标点通过映射方法到一根函数直线上。通过这种方法我们肯定会得到新的特征用来表示这个事件，新的特征剔除了原有特征的冗余信息，因此更有区分度。新的特征基于原有特征，它能够重建原有特征。主成分分析要保留最有可能重建原有特征的新特征，从而达到数据降维的作用。

例如我们得到了一个二维数据集，里面一个标签仅仅只用两个（ $x1,x2$ ）特征就能表示，但是我们只能用一个特征去描述这件事。在原始的 $x1,x2$ 坐标轴上，我们无论删掉 $x1$ 或者是 $x2$ 我们都不能完整的表达出这个点来。但是我们可以通过PCA，将数据从原来的坐标系转换到了新的坐标系，新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴的选择和第一个坐标轴正交且具有最大方差的方向。该过程一直重复，重复次数为原始数据中特征的数目。就通过该数据集（ $x1,x2$ ），我们通过该方法构建出 $(y1,y2)$ 坐标系，在该坐标系中我们可以发现数据基本都集中在 $y1$ 轴上面，而 $y2$ 这条短轴上则差距很小。在极端的情况，短轴如果退化成一点，那只有在长轴的方向才能够解释这些点的变化了；这样，由二维到一维的降维就自然完成了。

三、PCA算法推导

要详细了解PCA算法原理还是需要一定的数学基础的，不是那么容易理解推导出来的。但是可以尽可能的简化推导过程，但是还是有必须清楚掌握的数学知识。

1.投影

首先我们知道在笛卡尔直角坐标系中上面的点都可以用一个二维向量表示。当然如果是 $n$ 维向量可以等价表示为 $n$ 维空间中的一条从原点发射的有向线段，只不过就是很那表示。假设我们就在二维笛卡尔直角坐标系中，有

$A(x1,y1),B(x2,y2)$ ,那么在二维平面上A和B可以用两条发自原点的有向线段表示，如下图：

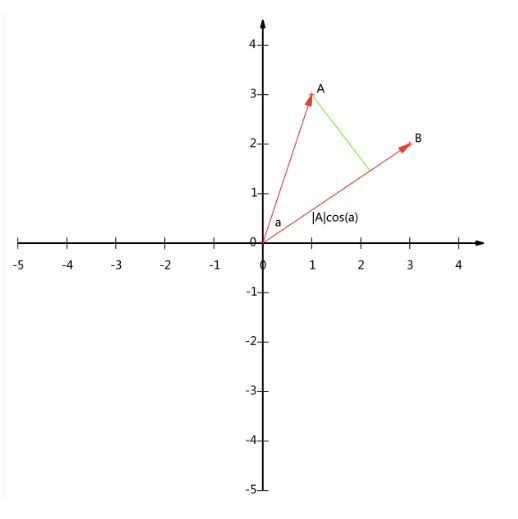
我们知道垂线与B的交点叫做A在B上的投影，再假设A与B的夹角为a，则投影的矢量长度为（这里假设向量B的模为1） $|A|cos(a)$ .

$|A|$ 就是A点的模，也就是A线段的标量长度。

而且我们知道： $A\cdot B=|A||B|cos(a)$ 。

如果B向量的模为1的话，我们就可以发现得到 $A\cdot B=|A|cos(a)$ .

2.基

一个二维向量可以对应二维笛卡尔直角坐标系中从原点出发的一条有向线段，对于（ $x1,x2$ ）来说，那么他们对应的坐标轴就是：

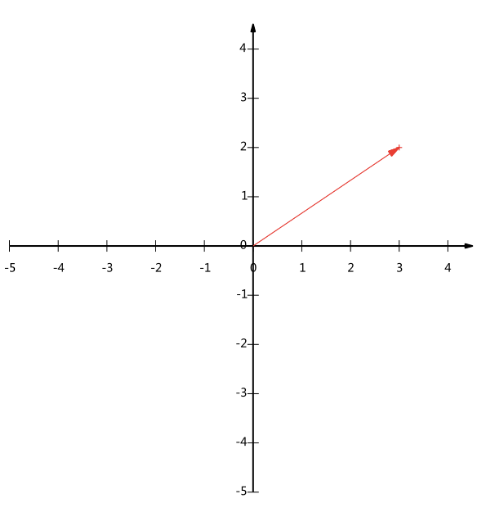
我们假设有一点 $(3,2)$ ，而它对应的向量就为从原点到 $(3,2)$ 的有向线段，而我们知道该向量在轴上的投影值3，在 $y$ 轴上的投影值为2。我们设该点为 $A$ 。

在 $x$ 轴上： $x\cdot A=|A||x|cos(a)$ ,而在 $x$ 轴上我们可以设它的模为1， $x$ 可为 $(1,0)$ .

在 $y$ 轴上： $y\cdot A=|A||y|cos(a)$ ,而在 $y$ 轴上我们可以设它的模为1， $y$ 可为 $(1,0)$ .

经过简单的数学变换，向量（ $x1,x2$ ）实际上表示线性组合：

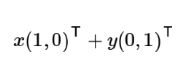
不难证明所有二维向量都可以表示为这样的线性组合，此处 $(1,0)$ 和 $(0,1)$ 叫做二维空间的一组基。

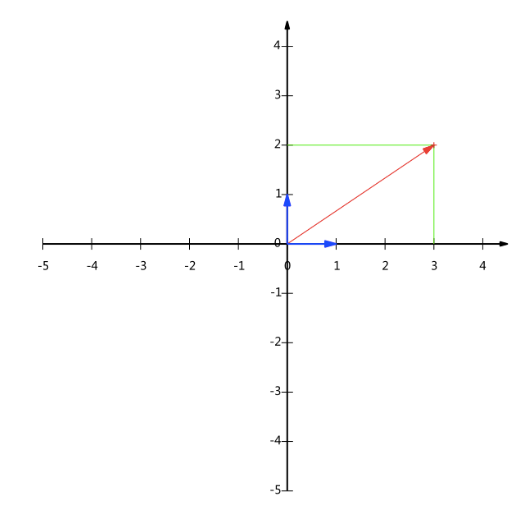
所以，要准确描述向量，首先要确定一组基，然后给出基所在的各个直线上的投影值，就可以了，只不过我们经常省略第一步，而默认以 $(1,0)$ 和 $(0,1)$ 为基。

当然我们也可以以其他向量为基底， $（1，1）$ $(1,1)$ 和 $(1,-1)$ 也可以成为一组基。

一般来说，我们希望基的模是1，因为从内积的意义可以看到，如果基的模式1，那么就可以方便的用向量点乘基而直接获得其在新基上的坐标了！实际上，对应于任何一个向量我们总可以找到其同方向上模为1的向量，只要让两个分量分别除以模就好了，例如上面的基就可以变为： $(1/\sqrt{2},1/\sqrt{2})$ , $(1/\sqrt{2},-1/\sqrt{2})$ 。

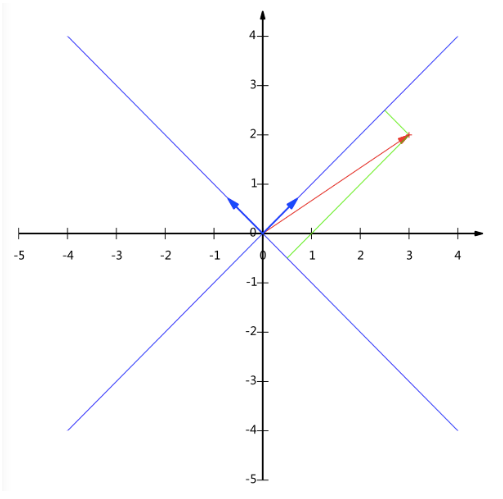
现在我们想获得 $(3,2)$ 在新基上的坐标，即在两个方向上的投影矢量值，那么根据内积的几何意义，我们只要分别计算 $(3,2)$ 和两个基的内积，不难得到新的坐标为( $(5/ \sqrt{2}, -1/\sqrt{2} )$ )。

3.基变换的矩阵表示

将 $(3,2)$ 变换为新基上的坐标，就是用 $(3,2)$ 与第一个基做内积运算，作为第一个新的坐标分量，然后用 $(3,2)$ 与第二个基做内积运算，作为第二个新坐标的分量。实际上，我们可以用矩阵想成的形式简洁的表示这个变换：

那么对于多个二维向量，例如（1,1），（2，2），（3,3）想变换到刚才那组基上，则可以变为这样：

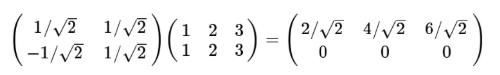
一般地，如果我们有M个N维向量，想将其变换为由R个N维向量表示的新空间中，那么首先将R个基按照行组成矩阵A,，然后将向量按照列组成矩阵B，那么两个矩阵的乘积AB就是变换结果，其中AB的第m列为A中的第M列变换后的结果。

　　数学表示为：

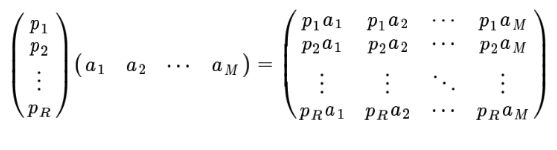
特别要注意的是，这里R可以小于N，而R决定了变换后数据的维数，也就是说，我们可以将一个N维数据变换到更低维度的空间中去，变换后的维度取决于基的数量，因此这种矩阵相乘的表示也可以表示为降维变换。

4.方差

现在我们知道可以通过将原始矩阵（特征集）通过投影的方式映射到不同的基底上从而构建新的特征，经过变换后达到降维的目的。而现在我们要知道如何选择正确的基底来帮助我们降维。

我们知道要使得向量经过投影之后更具有区分性，经过投影后要尽可能的分散。而这种分散程度，可以用数学上的方差来表述。

此处，一个字段的方差可以看做事每个元素与字段均值的差的平方和的均值，即：

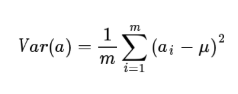
但如果每一次计算方差都要减去一个字段均值显然更加累赘。我们可以通过对数据的预处理使得字段的均值为0，例如我们的数据由五条记录组成，将它们表示为矩阵形式：

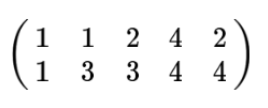
我们通过减去均值得到：

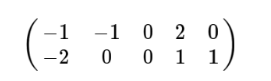
这样的话 $\mu$ 就为0了，因此方差可以直接用每个元素的平方和除以元素个数表示：

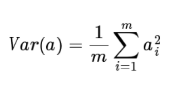
于是上面的问题被形式化表示为：寻找一个一维基，使得所有数据变换为这个基上的坐标表示后，方差值最大。

5.协方差

上述方法只能解决二维到一维的降维，但是对于多维数据我们第一步选择方差最大化的降第一维方式，那么我们第二步该如何选择呢？

如果我们还是单纯的只选择方差最大的方向，很显然，这个方向与第一个方向应该是“几乎重合在一起”，显然这样的维度是没有用的，因此应该有其他约束条件。

数学上可以用两个字段的协方差表示其相关性

是一种用来度量两个随机变量关系的统计量。
只能处理二维问题。
计算协方差需要计算均值。

由于已经让每个字段均值为0，则：

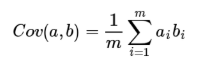
可以看出，在字段均值为0的情况下，两个字段的协方差简洁的表示为其内积除以元素数m。协方差的绝对值越大，则二个变量相互影响越大。

当协方差为0时，表示两个字段完全独立，为了让协方差为0，我们选择第二个即时只能在与第一个基正交的方向上选择。因此最终选择的两个方向一定是正交的。

　　至此，我们得到了降维问题的优化目标：将一组N维向量降维k维（K大于0，小于N），其目标是选择K个单位（模为1）正交基，使得原始数据变换到这组基上后，各字段两两间协方差为0，而字段的方差则尽可能大（在正交的约束下，取最大的k个方差）。

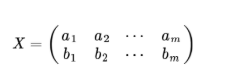
然后我们用X乘以X的转置，并乘上系数1/m：

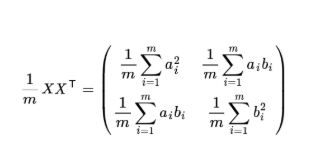
这时候我们会发现，这个矩阵对角线上的两个元素分别是两个字段的方差，而其他元素是a和b的协方差，两者被统一到了一个矩阵的。

根据矩阵相乘的运算法则，这个结论很容易被推广到一般情况：

设我们有m个n维数据记录，将其按列排成n乘m的矩阵X，设 $C= 1/m*X*XT$ ，则C是一个对称矩阵，其对角线分别是各个字段的方差，而第l行j列和j行i列元素相同，表示i和j两个字段的协方差。

6.协方差矩阵

　假设我们只有a和b 两个字段，那么我们将他们按行组成矩阵X：

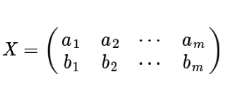
协方差矩阵能处理多维问题；
协方差矩阵是一个对称的矩阵，而且对角线是各个维度上的方差。
协方差矩阵计算的是不同维度之间的协方差，而不是不同样本之间的。
样本矩阵中若每行是一个样本，则每列为一个维度，所以计算协方差时要按列计算均值。

如果数据是3维，那么协方差矩阵是：

7.特征值与特征向量

对于 $Ax=\lambda x$ 也可以写作：

8.协方差矩阵对角化

设原始数据矩阵X对于的协方差矩阵为C，而P是一组基按行组成的矩阵，设Y=PX，则Y为X对P做基变换后的数据，设Y的协方差矩阵为D，我们推导一下D与C的关系：

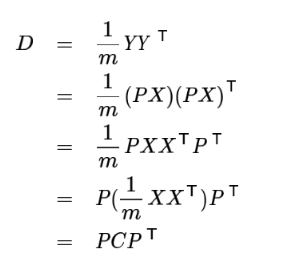
其实到这里快差不多了，优化目标变成了寻找一个矩阵P，满足PCPT是一个对角矩阵，并且对角元素按照从大到小依次排列，那么P的前K行就是要寻找的基，用P的前K行就是要寻找的基，用P的前K行组成的矩阵乘以X就使得X从N维降到了K维并满足上述优化条件。

协方差矩阵C是一个对称矩阵，在线性代数上，实对称矩阵有一系列非常好的性质：

实对称矩阵不同特征值对应的特征向量必然正交。
设特征向量 λ 重数为r，则必然存在r个线性无关的特征向量对应于 λ，因此可以将这r个特征向量单位正交化。

一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量，设这n个特征向量为e1, e2, ...en，我们将其按照列组成矩阵：

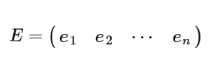
　则对协方差矩阵C有如下结论：

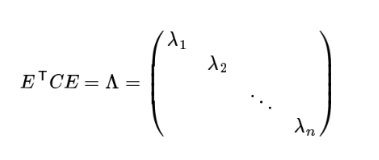
其中 Λ 为对称矩阵，其对角元素为各特征向量对应的特征值（可能有重复）。

到这里，我们发现我们已经找到了需要的矩阵P：

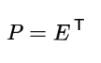
P是协方差矩阵的特征向量单位化后按照行排列出的矩阵，其中每一行都是C的一个特征向量，如果设P按照 Λ 中特征值从大到小，将特征向量从上到下排列，则用P的前K行组成的矩阵乘以原始数据矩阵X，就可以得到我们需要的降维后的数据矩阵Y。

至此，我们完成了整个PCA的数学原理讨论。

四、PCA运用流程

1）将原始数据按列组成n行m列矩阵X
2）将X的每一行（代表一个属性字段）进行零均值化（去平均值），即减去这一行的均值
3）求出协方差矩阵 C= 1/m*X*XT
4）求出协方差矩阵的特征值及对应的特征向量
5）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P（保留最大的k各特征向量）
6）Y=PX 即为降维到K维后的数据

将数据转换成前N个主成分的伪代码大致如下：

去除平均值
计算协方差矩阵
计算协方差矩阵的特征值和特征向量
将特征值从大到小排序
保留最上面的N个特征向量
将数据转换到上述N个特征向量构建的新空间中

from numpy import *
 
 
#从一个文本文件中读入一个数据集,数据集示例如下：
'''
8.805945	10.575145
9.584316	9.614076
11.269714	11.717254
9.120444	9.019774
7.977520	8.313923
'''
 
def loadDataSet(fileName, delim='\t'):
    fr = open(fileName)
    stringArr = [line.strip().split(delim) for line in fr.readlines()]
    datArr = [map(float,line) for line in stringArr]
    return mat(datArr)
 
	
#基于numpy实现pca算法	
def pca(dataMat, topNfeat=9999999):                           #原数据  m*n
    meanVals = mean(dataMat, axis=0)                          #均值：1*n
    meanRemoved = dataMat - meanVals 			              #去除均值  m*n
    covMat = cov(meanRemoved, rowvar=0)                       #协方差矩阵 n*n
    eigVals,eigVects = linalg.eig(mat(covMat))				  #特征矩阵  n*n
    eigValInd = argsort(eigVals)            #将特征值排序
    eigValInd = eigValInd[:-(topNfeat+1):-1]  #仅保留p个列（将topNfeat理解为p即可）   
    redEigVects = eigVects[:,eigValInd]       # 仅保留p个最大特征值对应的特征向量，按从大到小的顺序重组特征矩阵n*p
    lowDDataMat = meanRemoved * redEigVects		#将数据转换到低维空间lowDDataMat： m*p
    reconMat = (lowDDataMat * redEigVects.T) + meanVals    #从压缩空间重构原数据reconMat：  m*n
    return lowDDataMat, reconMat

参阅：

Python机器学习笔记：主成分分析（PCA）算法

https://baike.baidu.com/item/%E4%B8%BB%E6%88%90%E5%88%86%E5%88%86%E6%9E%90/829840?fromtitle=%E4%B8%BB%E6%88%90%E5%88%86%E5%88%86%E6%9E%90%E6%B3%95&fromid=2652206&fr=aladdin

PCA原理

均值，方差，协方差，协方差矩阵，特征值，特征向量

https://blog.csdn.net/wiborgite/article/details/83513234

张士玉小黑屋

当前位置：首页 » 《关于电脑》 » 正文

PCA（主成分分析法）原理以及应用+代码实现_master_hunter的博客

10 人参与 2021年03月12日 16:43 分类 : 《关于电脑》评论

前言

一、为什么需要PCA？（为什么要降维）

二、PCA简介

三、PCA算法推导

1.投影

2.基

3.基变换的矩阵表示

4.方差

5.协方差

6.协方差矩阵

7.特征值与特征向量

8.协方差矩阵对角化

四、PCA运用流程

评论（0）

赞助本站

最新文章

张士玉小黑屋

当前位置：首页 » 《关于电脑》 » 正文

PCA（主成分分析法）原理以及应用+代码实现_master_hunter的博客

10 人参与 2021年03月12日 16:43 分类 : 《关于电脑》 评论

前言

一、为什么需要PCA？（为什么要降维）

二、PCA简介

三、PCA算法推导

1.投影

2.基

3.基变换的矩阵表示

4.方差

5.协方差

6.协方差矩阵

7.特征值与特征向量

8.协方差矩阵对角化

四、PCA运用流程

评论（0） 赞助本站

最新文章

10 人参与 2021年03月12日 16:43 分类 : 《关于电脑》评论

评论（0）

赞助本站