转基因干饭迷宫老鼠

问题描述

相信大家应该很熟悉迷宫老鼠问题，也一定有相当多部分的人能够熟练地使用BFS求解迷宫老鼠的最短路径问题，那么，如果现在，我们对迷宫老鼠问题进行适当的强化，你是否还能熟练的求解这个问题：

问题1：

在传统迷宫老鼠问题的基础上，思考一下问题：转基因超级干饭老鼠可以在迷宫中斜着走，但是横向移动一下你需要喂它10斤饭，斜着走一下你需要喂它14斤饭（因为距离变成了根号2），你能输出这个超级迷宫老鼠干饭最少的路径和干饭吗？

问题2：

在问题1的基础上，如果迷宫里存在“水域”，“高地”等不同地形，老鼠分别需要消耗15，20斤饭才能移动一个地形，那么，又该如何求解这个问题？

问题分析

首先，你可能认为写出这个题目的人多多少少沾点儿脑瘫，但是，问题也并非空穴来风，这种行为其实是在游戏中非常常用的行为。试想在一个RTS或MOBA游戏中，游戏的地形很少有完全平坦的陆地。大多数情况下，游戏中不仅存在或多或少的障碍物，穿过不同的地形往往也意味着不同的代价。事实上，游戏中的寻路方法远远比我们接下来要讨论的算法复杂许多。

我不可以用BFS，DFS或者Dijkstra 算法吗？

不可以。

首先我们来探讨BFS：BFS是一个相当常用的算法，这个算法被广泛的应用在寻路，遍历图，求最短路径等多种图论算法中。他的核心思想是平等的探索起始点的各个方向。对于普通的迷宫问题而言，这种算法是求解最短路的优秀方法，然而，由于它平等探索的特性，决定了BFS无法在这种带有权值的问题中使用。

其次，我们来考察DFS算法：在本人的经验中，首先很少见到有人使用DFS来求解最短路径问题，不过DFS确实可以用来求最短路径。它面临的问题和BFS相同：DFS总是平等的对待所有的点，在这个问题中，图中每个节点却拥有不同的权值，因此，DFS算法并不适用这个问题。

最后，让我们观察Dijkstra算法，Dijkstra算法可以用来解决带有权值的问题。但是，Dijkstra算法的扩张方式是从启示点开始向四周扩张的，这对于程序的速度而言并不是一件好事，而游戏算法往往对速度具有极高的要求。

因此，我们应该考虑的最好算法，应该是既能考虑遍历方向应该是优先选择向结束点靠近的，同时，又能处理移动代价的算法。

A*算法

A*算法是用来干什么的？

寻路的
尽管我们发现以上讨论的三种方法并不适用于解决这个问题，但是我们一直以来的努力并非全部木大。我们依然能参考使用Dijkstra算法与BFS的思维，提出新的思路。在实践中，A算法被认为是一种高效而可行的算法，在接下来的部分中，我们将尝试使用A算法来解决转基因干饭老鼠问题1

A*算法如何工作

试看这幅地图：

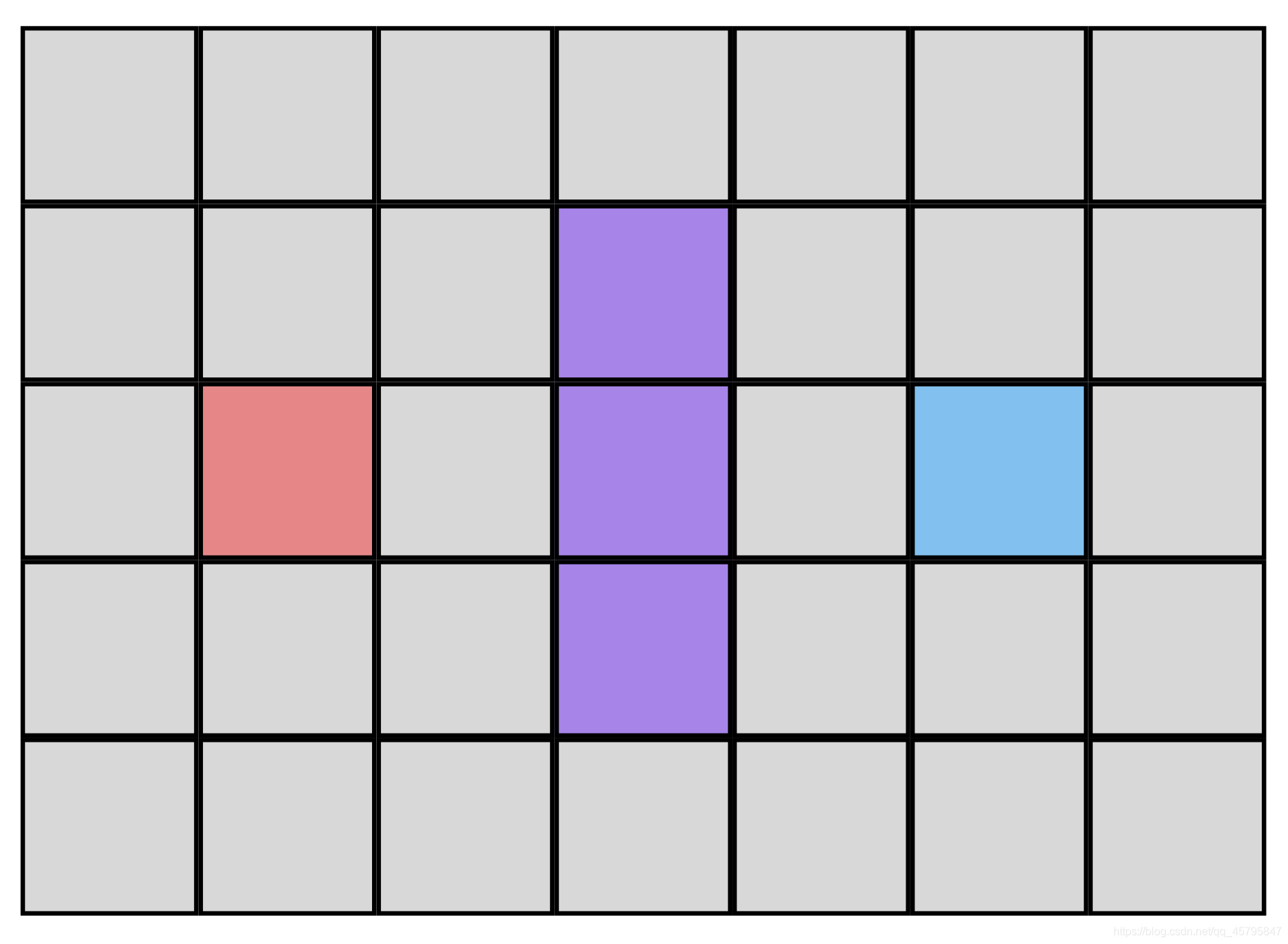
在这地图中，紫色地图块为障碍物，红色地图块为起点，蓝色地图块为结束点，其余地图块均为可到达区域，其他题设与问题1所描述的相同。

我们将以这幅地图为例介绍A*算法的使用方法，在此之前，我们需要明确我们将在此处使用的工具。

1.Open List：一个用于储存节点的数据结构，虽然他的名字叫Open List，但是使用线性表的等其他数据结构也可以。

2.Closed List：同Open List，一个用于储存节点的数据结构，使用链表，线性表等常见数据结构均可。

3.每个节点具有三个数值：
F： 满足 F = G + H。
G： 从起点开始，到指定格子的距离。
H： 从起点开始，到达这个格子的预计距离。

4.每个节点还应该具有一个父亲，你可以使用一个指向节点的指针表示，也可以使用简单的记录父亲坐标的方法表示。

看到这里估计大家并不知道这四个工具如何使用，没关系，我们开始搜索，边说边用：

开始工作！

0.输入各点的坐标，绘制地图，置空你的OpenList与ClosedList

1.第一步，从起点A开始，标记所有A周围的可以到达的点，并将他们全部加入OpenList，当然，这些点不可以本来就在OpenList或者ClosedList中。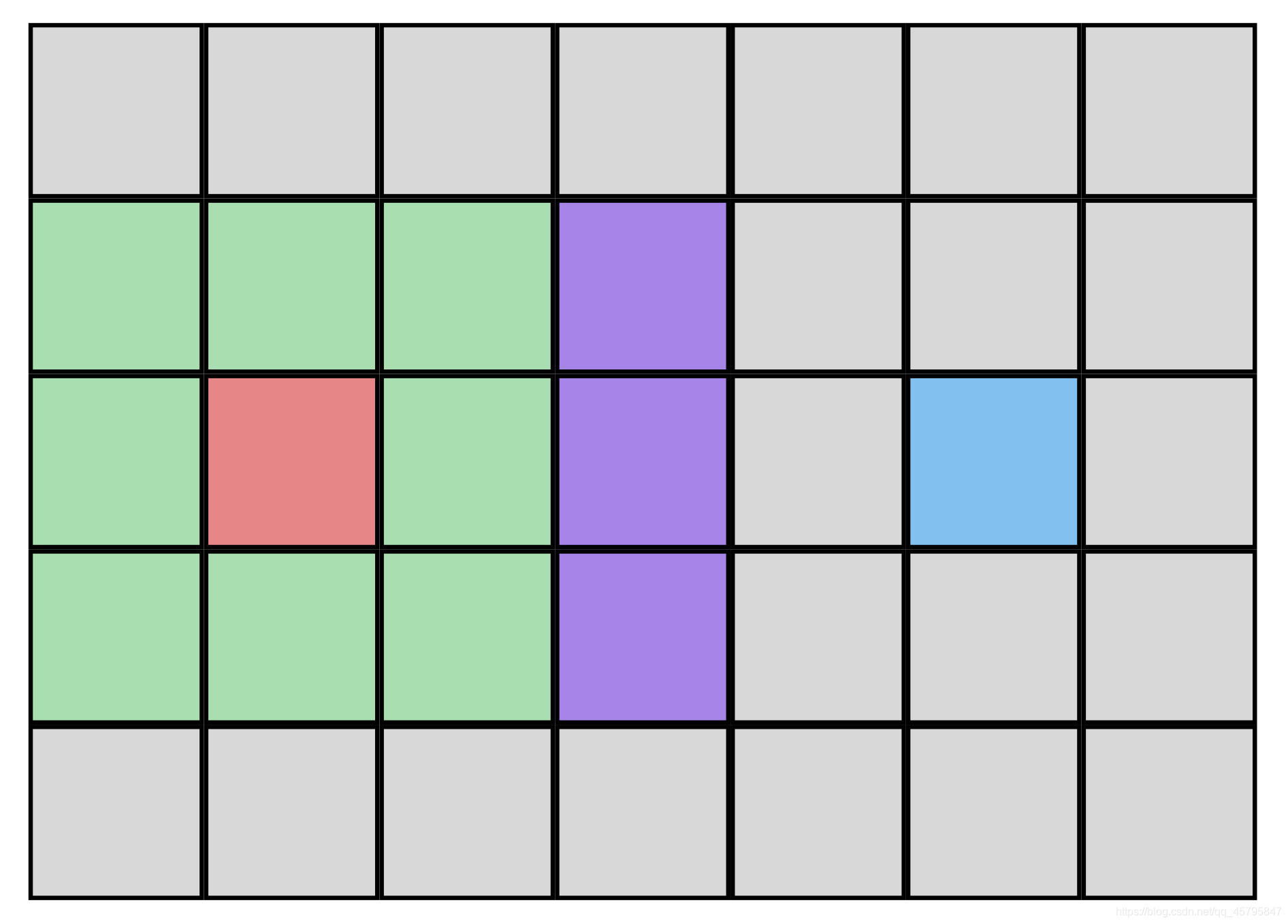
如图所示，所有绿色色块代表他们被加入了OpenList。

2.我们为所有的点都设置父亲，在这里，他们的父亲就是起始点，标记完父亲之后的图应该是这个样子的：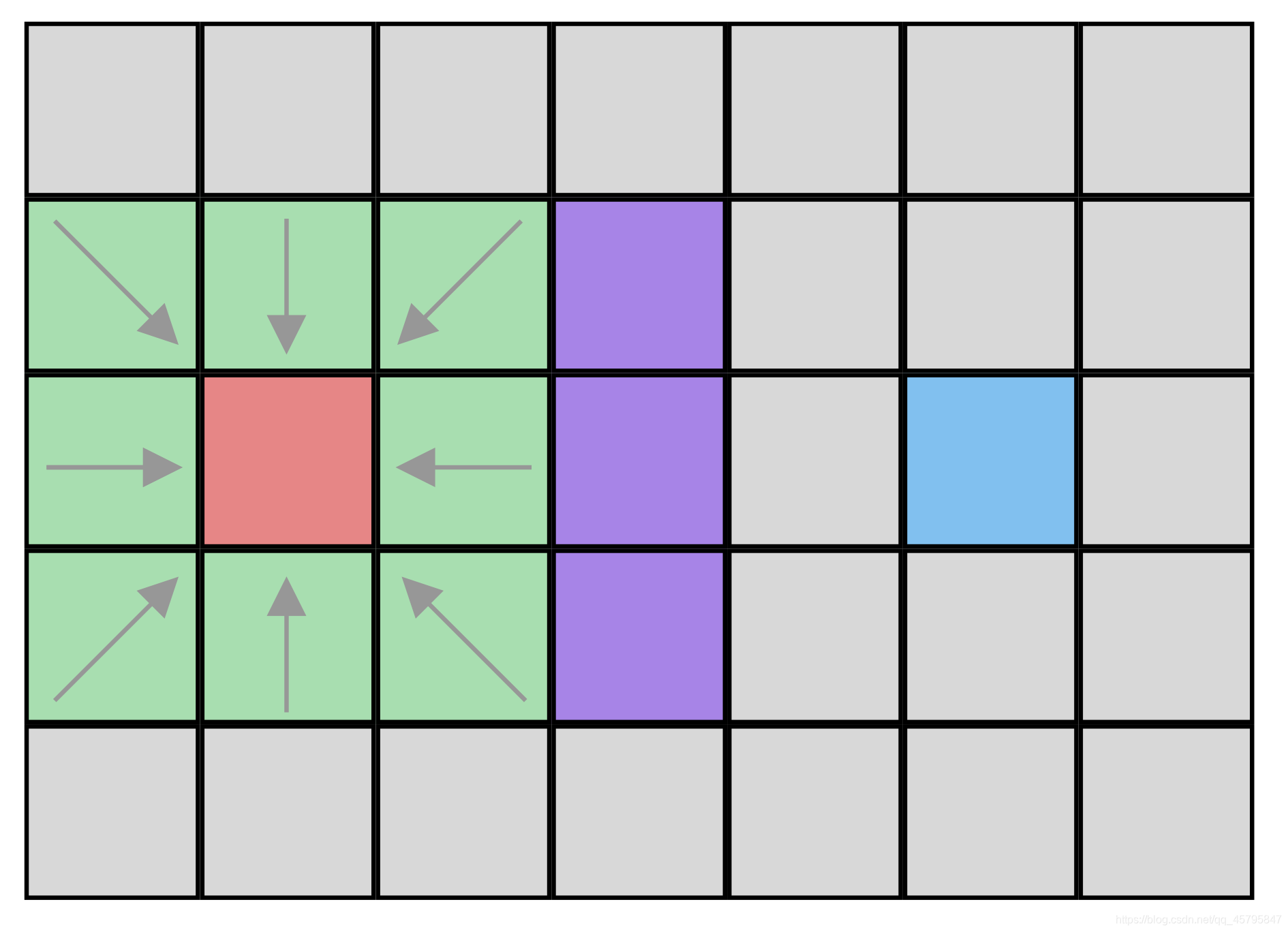
这一步是很有必要的，因为我们需要能够追踪这些点的父亲，来寻找这个路径。我们稍后将看到这个点所发挥的巨大作用。

3.下一步，我们需要选出一个点来，把这个点作为选中点，并把A加入到ClosedList中，不过，这里我们遇到了A*算法的一个关键问题：

我应该选择哪个点？

答案是：F值最小的那个，那么如何求F值呢？

如何求F值

F = G + H ！求F的过程就是一个求G和H的过程，我们首先来探讨简单的G

G怎么求？

G非常容易理解，他就是从A点开始到周围点的移动代价，我们在题设中已经说了，横向移动为10，斜向移动为14，很容易求起始点周围的个点的移动代价。注意：是到A的！不是到当前选中点的，在一轮循环中，应该等于 当前点的移动代价 + 10 或 当前点的移动代价 +14 ，并且这个值并不是对于一个点来说永远不变的，我们接下来将看到。

H怎么求

求H的方法是非常多变的，这里我们使用 Manhattan 方法，这个方法允许我们去估算当前点到终止点的距离，我们不妨设终止点的坐标分别为：
end_point_x与end_point_y，设当前点的坐标为current_point_x与current_point_y。在不同的地图中，用来计算H的公式并不是相同的，在这个地图中，这个公式是一种好方法：

H = abs(end_point_x - current_point_x) * 10 + abs(end_point_y - current_point_y) * 10;

这个距离是忽略代价与障碍的，因此，非常便于使用。

这只是一个估计值，并不是实际的距离。

在完成了以上的操作之后，我们就可以求得各个点的F值，我将他们的值全部标记在了地图上。

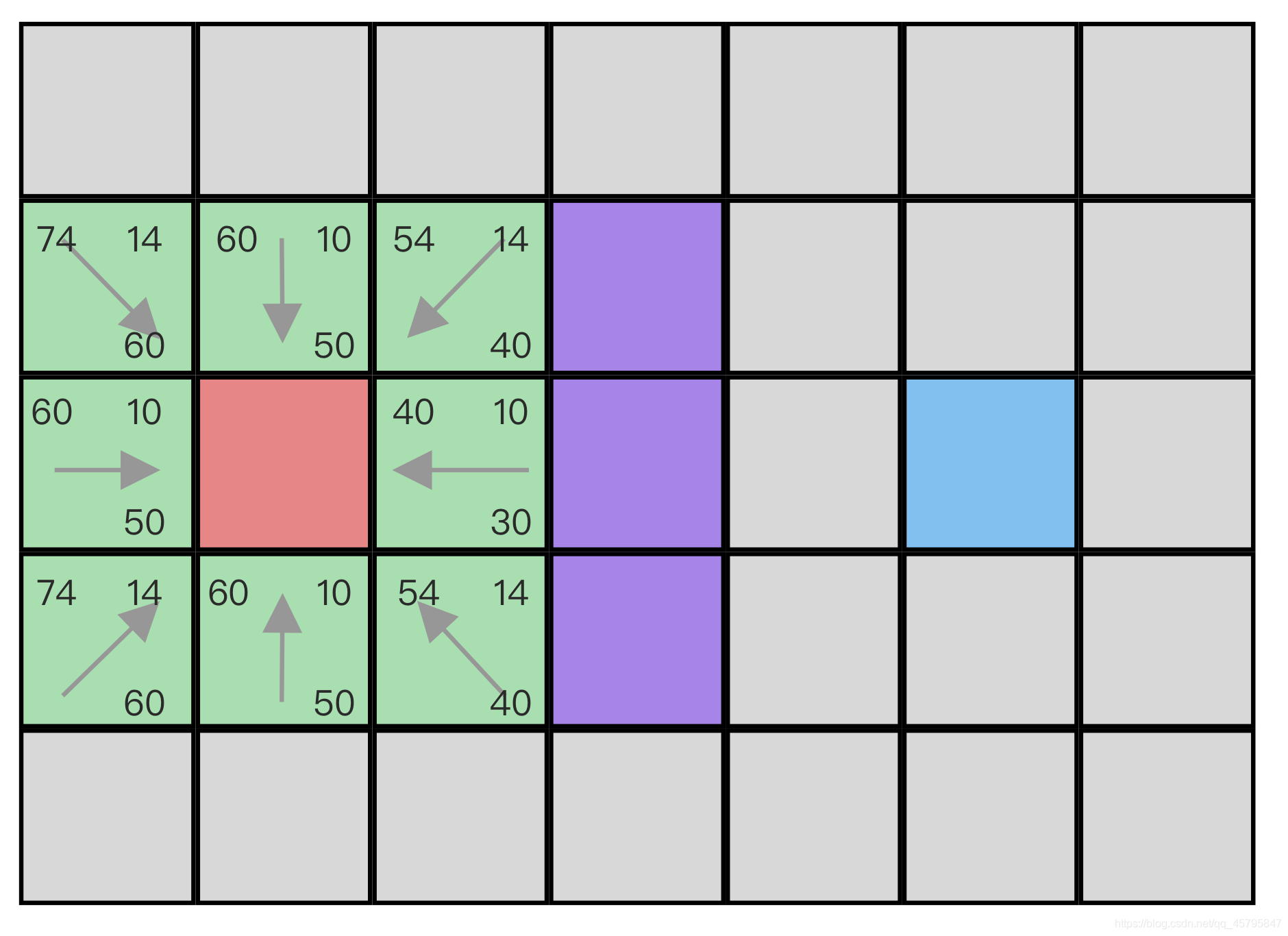
回到工作！

现在，我们已经求得了所有A邻近的点的F值，按照我们刚才所述，将A加入Closed List，在途中，我用黄色标记表示所有被加入Closed List的点，并且将最小F值得点标记为当前点，即current_point，我们使用红色点来将其标记：

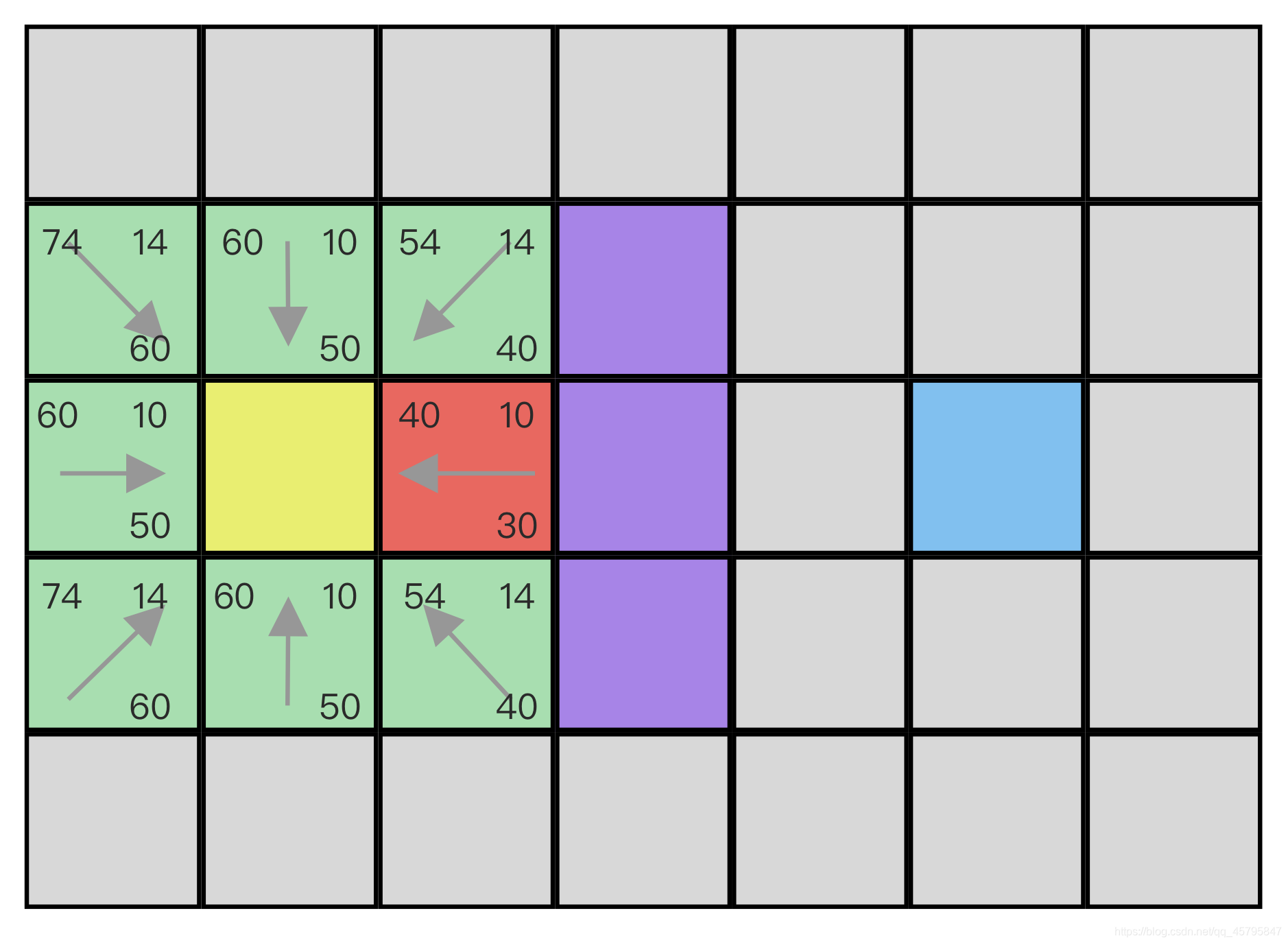
现在，重复1，2，3，把选中点周围的点可到达的，不在OpenList的，不在ClosedList的点，全部加入Open List中，一般来说，不会更新各个点的父亲，但是，在求F，G，H这里一定要非常非常注意：如果通过当前点到达临界点的方式会造成一个更小的G值，那么，需要更新G，F，与父亲。我们在本轮循环中，这一点没有被使用，我们考察接下来的下一步循环结果：

注意！我们设定不可以逾越墙角！因此红色点的右下角不可以到达！实际上你可以删除这个设定，这里加入是为了方便讲解

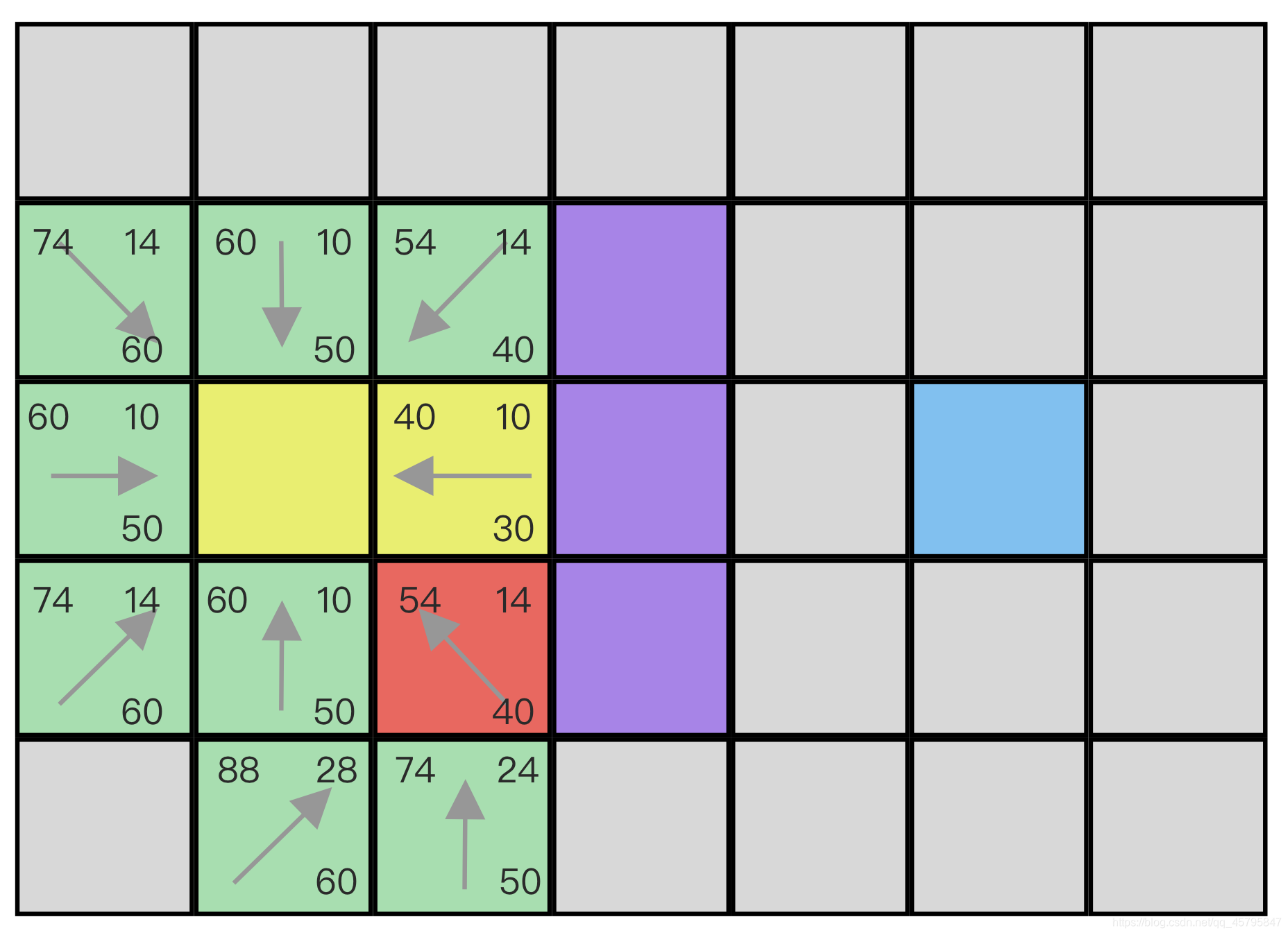
看下一轮循环：

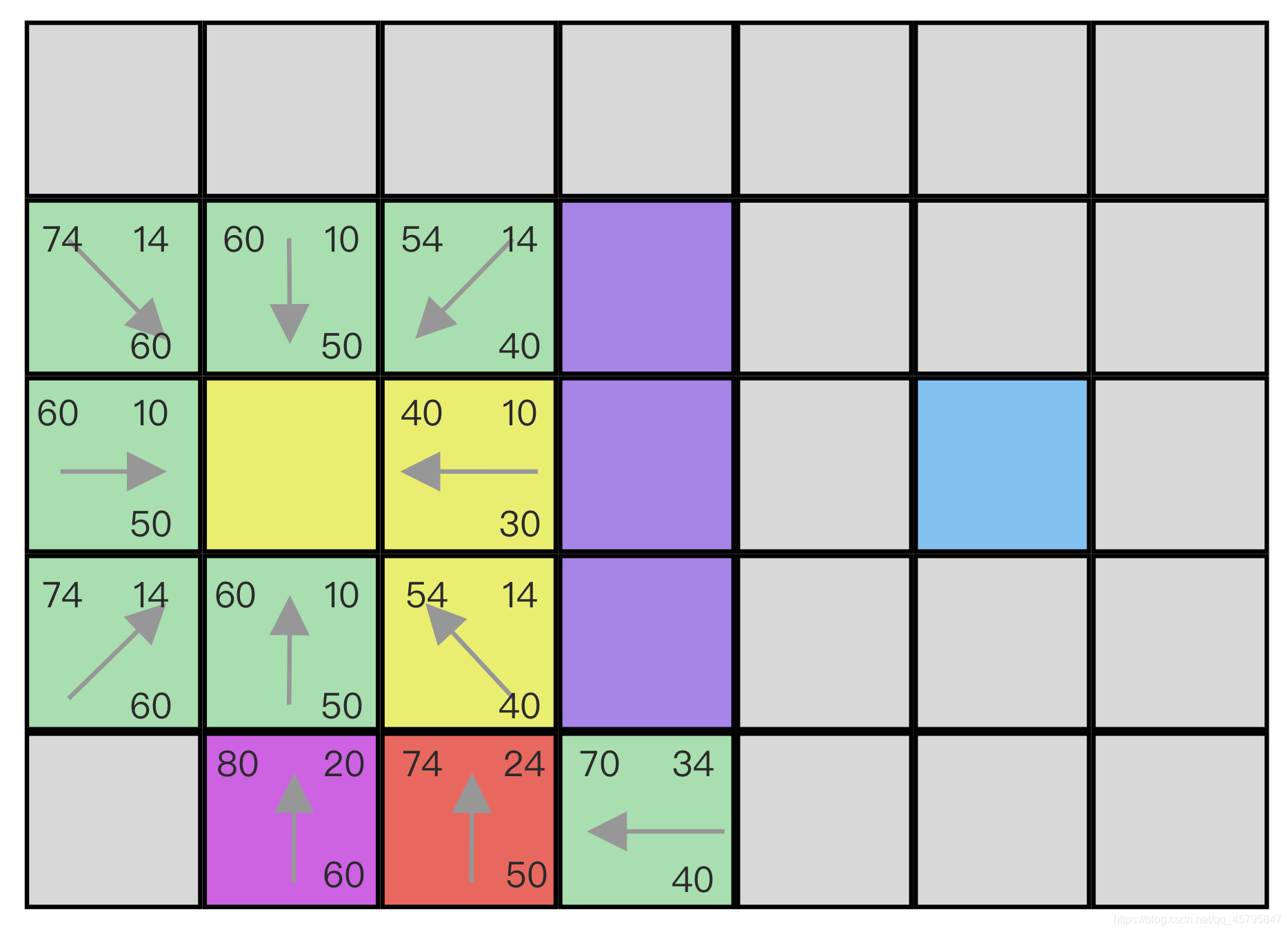
注意当前点左边这个点，他的G值被更新了，父母也被指向了它上面的格子，诸位可以试想一下，这件事情实际上在这个循环中发生了吗？很遗憾。没有。如果从当前的格子看，那么这个粉色的格子应该的G是24+10 = 34，要小于上一轮循环的得到的G，因此他的G，F，父母应该是没有被更新的。

那么为什么我要更新这个点？如果你选中粉色的格子的正上方那个点，那么这个点肯定就需要被更新，更新G，F与父母是A*算法中很重要的一点，但是我们选择的样例不太好，没有体现出来，在接下来的图中，这个点会被保持是没有更新的状态，请大家注意。

我们继续循环，直到结束点加入Open List，注意，请不要忘记我们不能逾越墙角的约定，此时图的状态应该是：

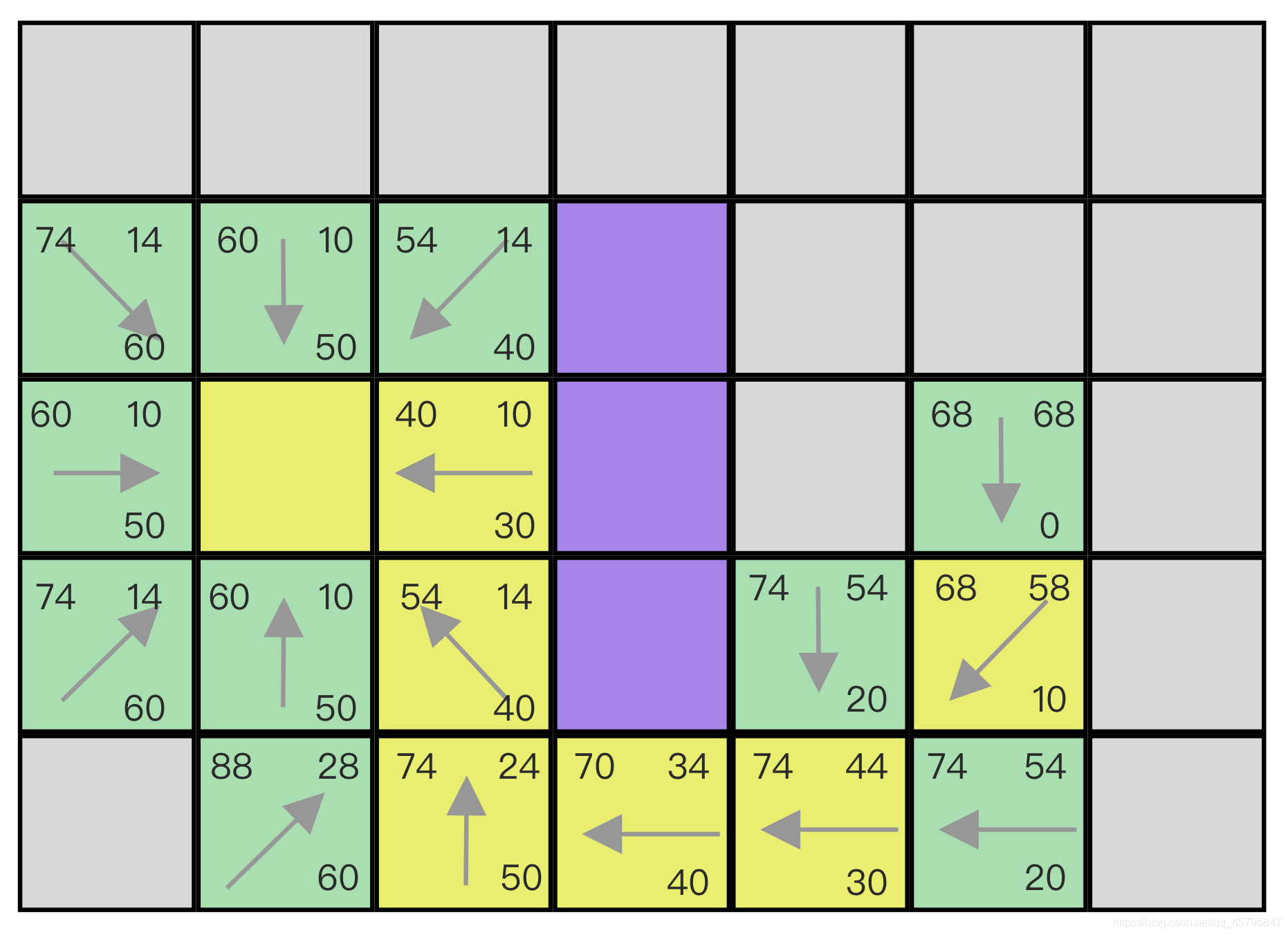
至此，结束点被加入Open List，顺着他的父亲，我们就可以找到最短路径，其G值就是最小的消耗值，我们把最短路径标记出来：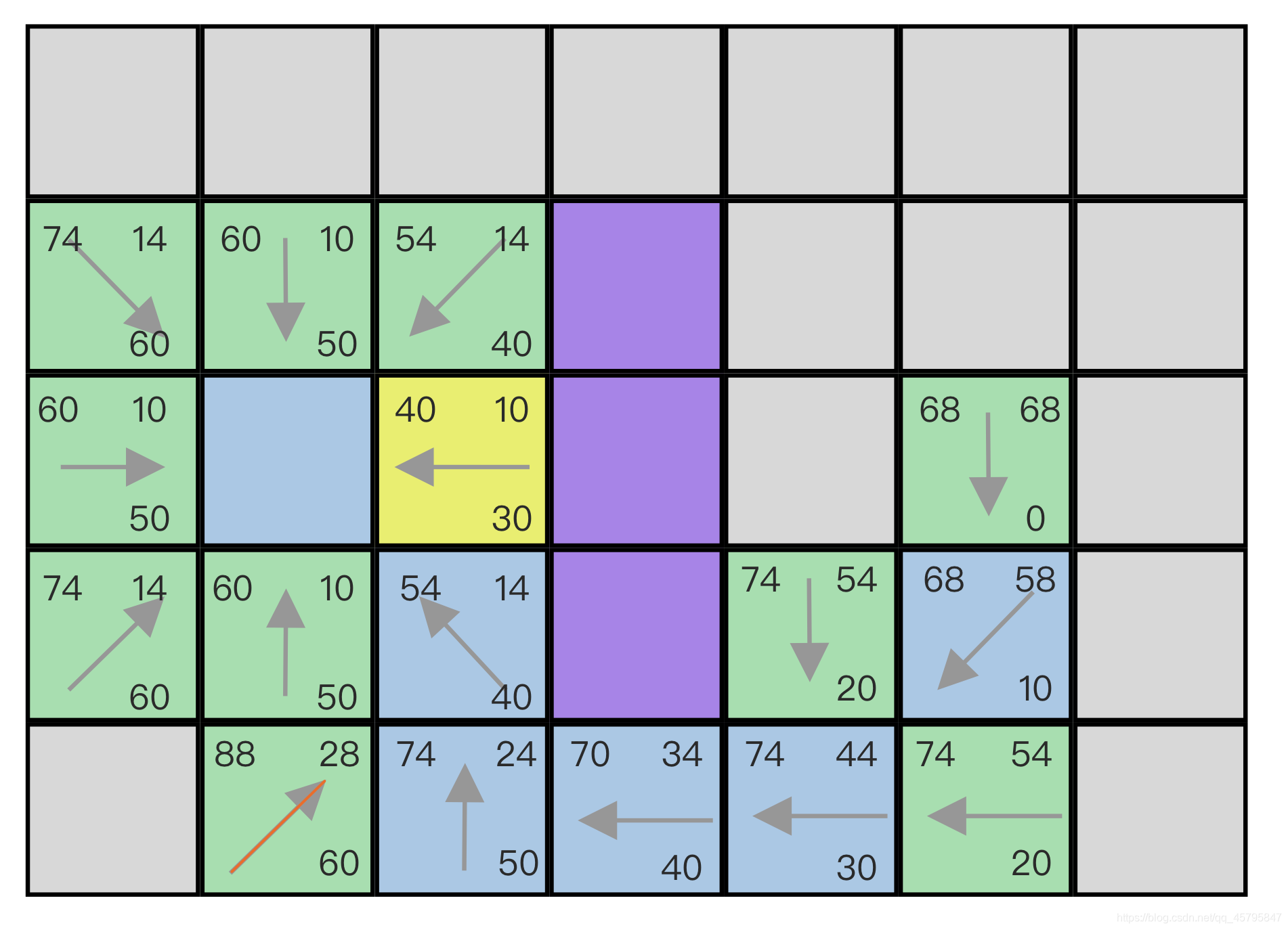
蓝色的路径即为最短路径！

代码实现（C++）

注意！以下代码在代码规范方面存在严重问题，语法组织不佳，且仅进行了部分小数据集验证，请谨慎使用！
注意！以下代码在代码规范方面存在严重问题，语法组织不佳，且仅进行了部分小数据集验证，请谨慎使用！
注意！以下代码在代码规范方面存在严重问题，语法组织不佳，且仅进行了部分小数据集验证，请谨慎使用！
(但是算法原理肯定是没问题的)

//
//  main.cpp
//  A*算法与迷宫干饭老鼠
//
//  Created by 讨狐之猛将 on 2021/3/22.
//

#include <iostream>
#include <vector>
#include <list>
#include <cmath>

/*
 转基因超级干饭老鼠可以在迷宫中斜着走，但是横向移动一下你需要喂它10斤饭，斜着走一下你需要喂它14斤饭（因为距离变成了根号2），你能输出这个超级迷宫老鼠干饭最少的路径和干饭吗？
 测试地图见：
 https://blog.csdn.net/hitwhylz/article/details/23089415
 */

using std::cin;
using std::cout;
using std::endl;
using std::vector;
using std::list;

struct node{
    
    int parent_x;
    int parent_y;
    int x_;
    int y_;
    int G;
    int F;
    int H;
    bool barrier;
    
    node(int x=0, int y=0):x_(x),y_(y){
        G = 0;
        F = 0;
        H = 0;
        barrier = false;
        parent_x = -1;
        parent_y = -1;
    }
    
};

int dx[] = {0,0,1,-1,1,-1,-1,1};
int dy[] = {1,-1,0,0,1,-1,1,-1};

int map_row;
int map_col;

vector<vector<node> >map;
vector<node> open_list;
vector<node> closed_list;

//判断相邻点是否在open_list
bool in_open_list(node n,int dx,int dy){
    
    bool In_list = false;
    
    for(vector<node>::iterator i = open_list.begin(); i!= open_list.end(); i++){
        if(i->x_ == n.x_ + dx && i->y_ == n.y_ + dy)
            In_list = true;
    }
    
    return In_list;
}

//判断相邻点是否可以加入open_list
bool Judge(node n,int dx,int dy){
    bool In_list = false;
    
    for(vector<node>::iterator i = open_list.begin(); i!= open_list.end(); i++){
        if(i->x_ == n.x_ + dx && i->y_ == n.y_ + dy)
            In_list = true;
    }
    
    for(vector<node>::iterator i = closed_list.begin(); i!= closed_list.end(); i++){
        if(i->x_ == n.x_ + dx && i->y_ == n.y_ + dy)
            In_list = true;
    }
    
    if(n.x_ + dx > 0 && n.y_ + dy > 0 && n.x_ + dx <= map_row && n.y_ + dy <=map_col && map[n.x_+dx][n.y_+dy].barrier == false && !In_list)
        //超出地图边界的不可以，障碍物不可以
        return true;
    
    return false;
}

int main(int argc, const char * argv[]) {
    
    //初始化地图信息
    std::ios::sync_with_stdio(false);
    
    int start_point_x;
    int start_point_y;
    int end_point_x;
    int end_point_y;
    int barrier_x,barrier_y;
    
    cin>>map_row>>map_col;
    cin>>start_point_x>>start_point_y;
    cin>>end_point_x>>end_point_y;
    
    for(int i = 0; i <= map_row; i++){
        map.push_back(vector<node>(map_col+1));
    }
    
    for(int i = 1; i<=map_row; i++){
        for(int j = 1; j<=map_col; j++){
            map[i][j].x_ = i;
            map[i][j].y_ = j;
        }
    }
    
    while(cin>>barrier_x>>barrier_y){
        
        if(barrier_x == -1 && barrier_y == -1)
            break;
        
        map[barrier_x][barrier_y].barrier = true;
    }
    
    //将起始点加入open_list
    open_list.push_back(map[start_point_x][start_point_y]);
    node& cc_node = map[start_point_x][start_point_y];
    
    //计算起始点的H
    map[cc_node.x_][cc_node.y_].H = abs(map[cc_node.x_][cc_node.y_].x_ - end_point_x) * 10 + abs(map[cc_node.y_][cc_node.y_].y_ - end_point_y) * 10;
    
    while (true) {
        
        for(int i = 0; i<8; i++){
            
            int G_new;
            
            if(Judge(cc_node, dx[i], dy[i])){
                //设置不在open_list的点的父亲
                if(!in_open_list(cc_node,dx[i],dy[i])){
                    map[cc_node.x_ + dx[i]][cc_node.y_+dy[i]].parent_x = cc_node.x_;
                    map[cc_node.x_ + dx[i]][cc_node.y_+dy[i]].parent_y = cc_node.y_;
                    
                    
                    //将符合要求的点加入open_list，如果不在open_list，设置他们的父亲
                    open_list.push_back(map[cc_node.x_ + dx[i]][cc_node.y_+dy[i]]);
                    
                    //如果end_point结束点被加入open_list,跳出循环，已找到最短路。
                    if(open_list.back().x_ == end_point_x && open_list.back().y_ == end_point_y)
                        break;
                }
                
                
                //计算这个点周围点的H
                map[cc_node.x_ + dx[i]][cc_node.y_+dy[i]].H = abs(map[cc_node.x_ + dx[i]][cc_node.y_+dy[i]].x_ - end_point_x) * 10 + abs(map[cc_node.y_ + dx[i]][cc_node.y_+dy[i]].y_ - end_point_y) * 10;
                
                if(abs(dx[i]-dy[i])==1)//是一个上下左右移动
                    G_new = cc_node.G + 10;
                else//是一个斜向移动
                    G_new = cc_node.G + 14;
                
                //判断点是否之前加入过open_list，如果没有，更新G
                if(map[cc_node.x_ + dx[i]][cc_node.y_+dy[i]].G == 0)
                    map[cc_node.x_ + dx[i]][cc_node.y_+dy[i]].G = G_new;
                
                else{
                    //之前该点的G已经被确定过，那么他在open_list中
                    if(in_open_list(cc_node,dx[i],dy[i]) && map[cc_node.x_ + dx[i]][cc_node.y_+dy[i]].G > G_new){//新G比老G小
                        //更新G
                        map[cc_node.x_ + dx[i]][cc_node.y_+dy[i]].G = G_new;
                        
                        //重设父亲
                        map[cc_node.x_ + dx[i]][cc_node.y_+dy[i]].parent_x = cc_node.x_;
                        map[cc_node.x_ + dx[i]][cc_node.y_+dy[i]].parent_y = cc_node.y_;
                    }
                }
                
                //一轮循环更新完G之后，计算点的F
                map[cc_node.x_ + dx[i]][cc_node.y_+dy[i]].F = map[cc_node.x_ + dx[i]][cc_node.y_+dy[i]].G + map[cc_node.x_ + dx[i]][cc_node.y_+dy[i]].H;
                
            }
        }
        //将该点放入closed list，移出open list;
        open_list.erase(std::find_if(open_list.begin(), open_list.end(), [cc_node](node a){
            return a.x_ == cc_node.x_ && a.y_ == cc_node.y_;
        }));
        closed_list.push_back(cc_node);
        
        int n_x = open_list.front().x_;
        int n_y = open_list.front().y_;
        int current_smallest_F = map[n_x][n_y].F;
        
        for(vector<node>::iterator i = open_list.begin(); i != open_list.end(); i++){
            int round_F = map[i->x_][i->y_].F;
            if(round_F < current_smallest_F){
                current_smallest_F = round_F;
                n_x = i->x_;
                n_y = i->y_;
            }
            
        }
        
        cc_node = map[n_x][n_y];
        
        //如果end_point被加入了open_list 结束循环
        if(open_list.back().x_ == end_point_x && open_list.back().y_ == end_point_y)
            break;
        
    }
    
    node temp = map[end_point_x][end_point_y];
    
    vector<std::pair<int, int> >ans;
    ans.push_back(std::make_pair(end_point_x, end_point_x));
    
    while (temp.parent_x != start_point_x || temp.parent_y != start_point_y) {
        
        int next_x = temp.parent_x;
        int next_y = temp.parent_y;
        ans.push_back(std::make_pair(temp.parent_x, temp.parent_y));
        temp = map[next_x][next_y];
        
    }
    
    ans.push_back(std::make_pair(start_point_x, start_point_y));
    
    for(const auto& e : ans){
        cout<<"("<<e.first<<" , "<<e.second<<")"<<endl;
    }
    
    return 0;
    
}

延伸讨论

我们讨论了A*算法的一种模式，然而，实际游戏中，往往会产生更多问题，包括但不限于：

1.如果我一次选中的多个单位，那么我们需要让每一个单位都寻路吗？你可能会说我们只需要求一个单位的即可，其他单位顺着求得的路径来，那么，如果两个单位相离较远呢？如果设置一个距离界限，让超过距离界限的两个单位独立寻路，那么，怎么设定这个界限呢？如果你选中的单位里有海军和陆军，寻找不同的路径呢？

2.游戏中的路径并不是固定的，如果一个不可逾越的单位占据了目标格子，或者另一个玩家在寻得的路径上建立了一个建筑物，得到的最短路径还可以使用吗？或者如果地图是动态的，一些容易低代价的格子会动态的变成高代价的，那么，能否将A*改造为一个动态算法？

3.你的地图往往是十分巨大的，在一张巨大的地图上，如果把它们划分成1x1的格子使用A算法是很费时的，那么，是不是距离很远的点我们可以先设置为大格子，距离接近时我们设置为小格子呢？我们如何改进A算法可以得到类似的效果。

4.如果你的地图不是方形的，而是六边形的，你如何使用A*算法来求得最短路径呢？你的算法能否适配不同不规则图形的地图？

5.你选择的路径是直来直去的，是否有一种方法，能把A*算法得到的路径换为平滑的路径，让单位的移动更加自然呢？你该如何改进你的算法？

希望这篇文章能够帮到你，如有错误，烦请联系作者。

以上，刍荛之见，伏候卓裁。

原文地址：https://link.csdn.net/?target=http%3A%2F%2Fwww.gamedev.net%2Freference%2Farticles%2Farticle2003.asp
参考：https://blog.csdn.net/hitwhylz/article/details/23089415