目录
题目：三数之和
1. 题目解析
2. 算法原理
①. 暴力枚举
②. 双指针算法
不漏的处理：
去重处理：
固定一个数 a 的优化：
3. 代码实现
Ⅰ. 暴力枚举（会超时 O（N³））
Ⅱ. 双指针算法 （O（N²））
题目：三数之和
1. 题目解析
题目截图：
题目中所述的顺序不重要有两种情况：
最终选出来的几个三元组里，每个三元组里的数据顺序，是可以不用考虑的。
最终选出来的几个三元组，三元组的顺序，也是可以不用考虑的。
题目中还要求元素不能相同：
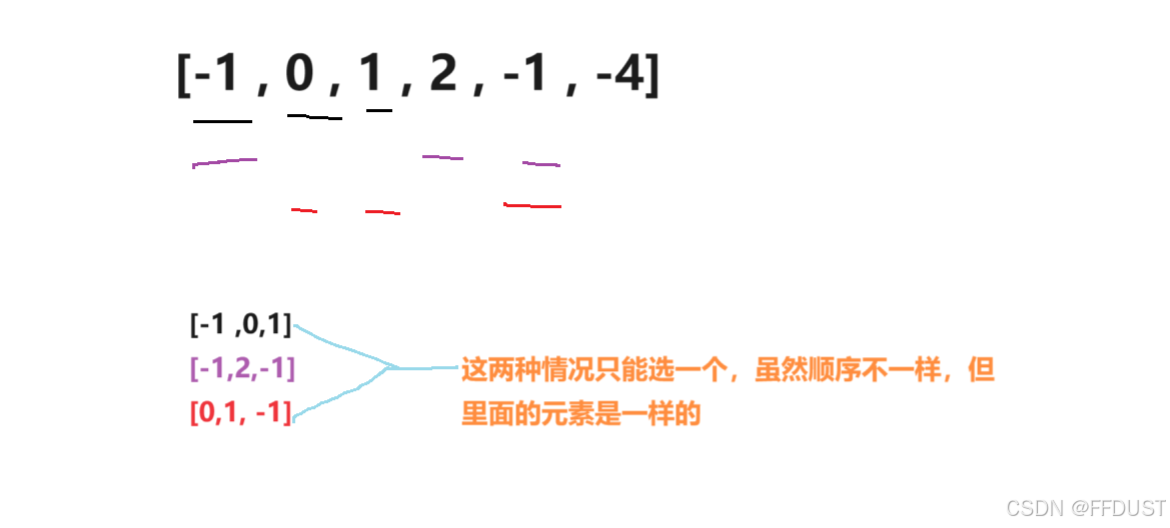
题目的细节要求也就是：
最终选出来的几个三元组里面的元素是对应不同的 返回的三元组及其三元组里的数据的顺序不重要。
题目给的示例二就是没有最终结果的情况
2. 算法原理
这道题有两种解法：
暴力枚举（但会超时）双指针算法①. 暴力枚举
虽然暴力枚举会超时，这里还要介绍一下的，因为双指针解法就是基于暴力枚举进行优化的。
这里方法就是：排序+暴力枚举（从左往右）+去重
这里排序去重要注意的是：
所以可以换个策略，先对原数组整个排序：
所以，也就是先排序，再暴力枚举（从左往右枚举），再去重。
这样套三个for循环就可以暴力枚举结果了
//伪代码演示for (int i = 0; i < n;) // 固定一个数a{ for (int j = i + 1; j < n;) //依次固定枚举第二个数 { for (int k = j + 1; k < n;) //枚举第三个数 { //查找符合的三元组，去重... } } }（这里去重在下面双指针解法解释），这里套了三个for循环时间复杂度：O（N³）。
②. 双指针算法
这里双指针算法的解决方法就是：排序+双指针+去重
排序同上面暴力枚举，都先对一整个数组排序，再进行下面的处理。
这里举例一个已经排过序的新数组：
我们先固定一个数，这里先固定第一个数：
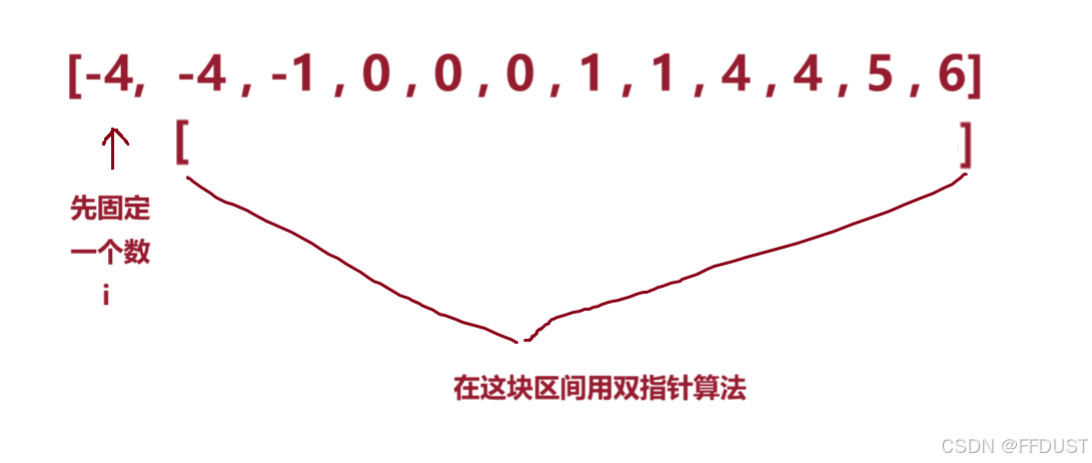
这里就转化成了和为s的两个数的问题，这里的s就是这个固定的数的相反数。也就是：
所以这里解决步骤：
先对整个数组排序固定一个数 a（这里有个小优化，后续介绍）在该数后面的区间内，利用双指针算法快速找到两个数的和为 -a 的即可。注意：这里只是找到了符合条件的情况，并没有去重。
接下来就是处理细节问题了，也就是去重和确保所有符合条件的情况不落下（后面简称不漏） 。
和为s的两个数（这里会用到，详细介绍在此链接）
不漏的处理：
先控制指针找到符合情况：
这时可以看到是找到符合的情况了：
接下来就需要调整：
所以，也就是找到一种结果之后，不要停（两个指针不停），缩小区间（两指针都向内移动一步），继续寻找符合的情况。
去重处理：
去重要考虑两种情况：
找到一种结果之后，left和right指针要跳过重复的元素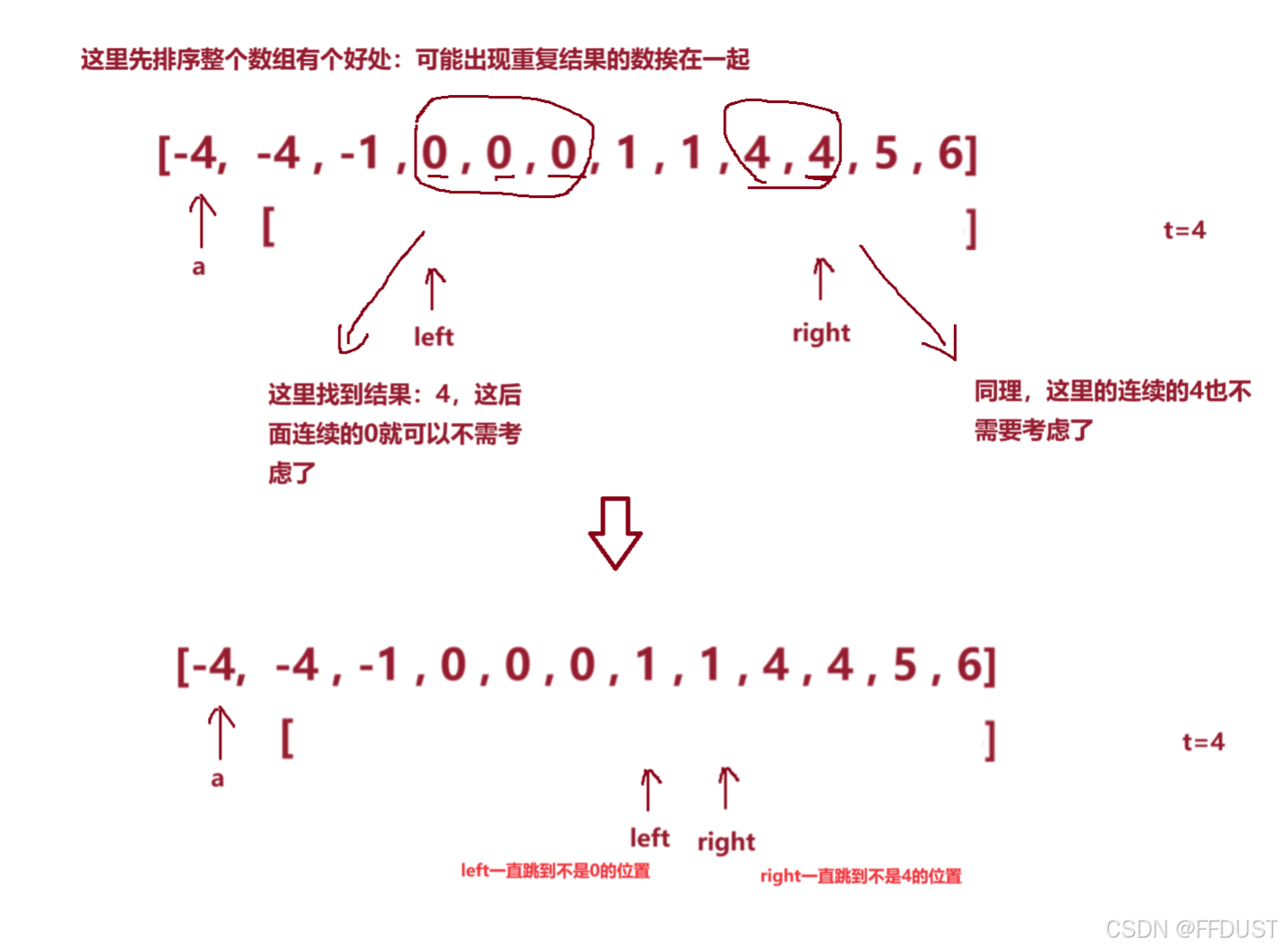
（这里也就把第一个4给枚举完了）。
但这里固定的 a 还是为-4，再继续枚举，是肯定都是重复结果的。所以当使用完一次双指针算法后，a也需要跳过重复的元素。
这里去重可能指针会越界，为了避免越界：
这里的越界问题不止对整个数组区间的越界，还有对要用双指针处理的区间可能会越界。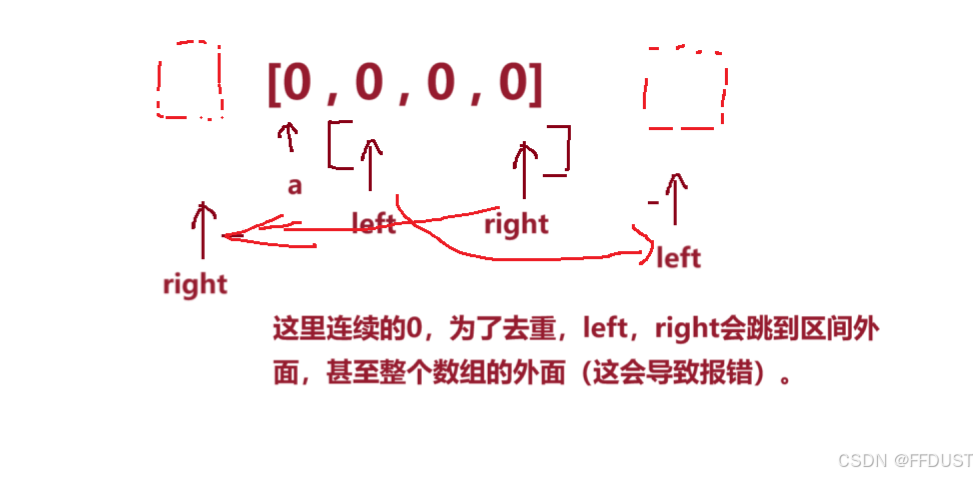
在实现去重代码时需要加个判断条件就可以解决：
要判断处理这个条件,既可避免越界if(left < right) 也就判断两个指针是否在相遇前固定一个数 a 的优化：
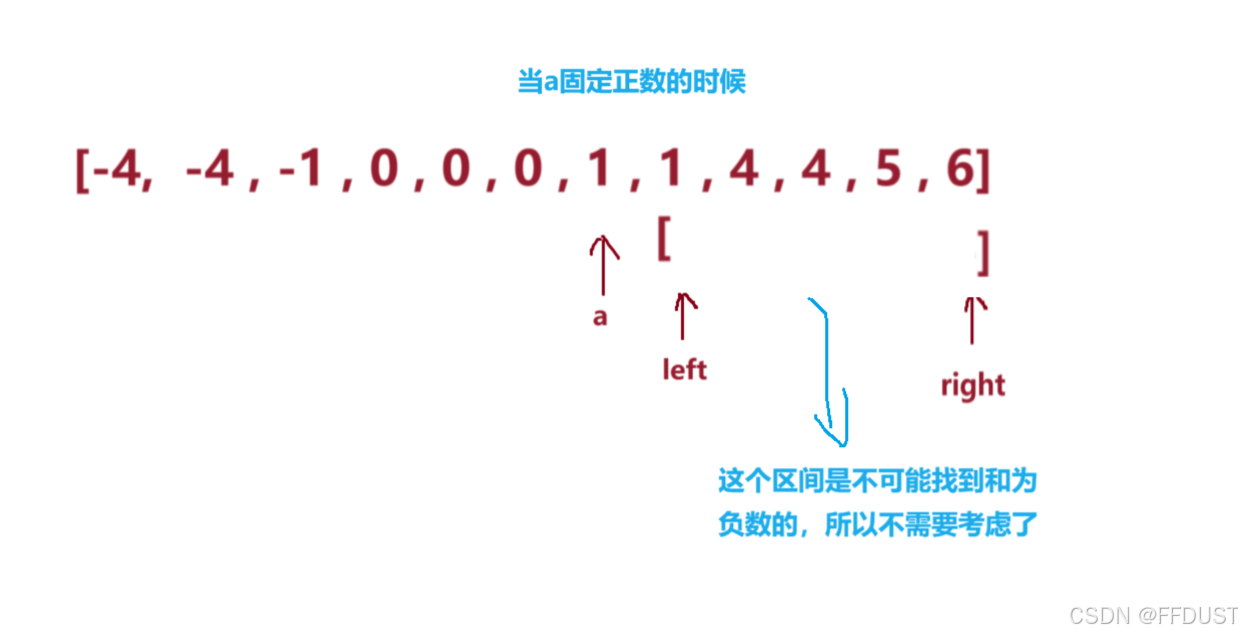
因为我们前面先排序该数组为升序了，所以固定数a就可以仅仅需要保证它≤0即可。
if (nums[i] > 0){ break; // 小优化，数a为正数情况不用考虑，是一定不成立的}接下来实现代码。
3. 代码实现
题目链接：三数之和
Ⅰ. 暴力枚举（会超时 O（N³））
class Solution {public: vector<vector<int>> threeSum(vector<int>& nums) { // 1.排序 sort(nums.begin(), nums.end()); vector<vector<int>> ret; // 用来存储所有的三元组 // 2.暴力枚举 int n = nums.size(); int i, j, k; for (i = 0; i < n;) // 固定一个数a { for (j = i + 1; j < n;) //依次固定枚举第二个数 { for (k = j + 1; k < n;) //枚举第三个数 { int sum = nums[i] + nums[j] + nums[k]; if (sum == 0) { ret.push_back({ nums[i],nums[j],nums[k] }); } //去重 ++k; while (k < n && nums[k] == nums[k - 1]) { ++k; } } //去重 ++j; while (j < n && nums[j] == nums[j - 1]) { ++j; } } //去重 ++i; while (i < n && nums[i] == nums[i - 1]) { ++i; } } return ret; }};提交记录：
测试用例：
Ⅱ. 双指针算法 （O（N²））
class Solution {public: vector<vector<int>> threeSum(vector<int>& nums) { // 1.排序 sort(nums.begin(), nums.end()); vector<vector<int>> ret; // 用来存储所有的三元组 // 2.利用双指针解决 int n = nums.size(); for (int i = 0; i < n;) // 固定一个数a { if (nums[i] > 0) { break; // 小优化，数a为正数情况不用考虑，是一定不成立的 } // 定义left，right，target通过双指针获取相加等于0的组合 int left = i + 1, right = n - 1, target = -nums[i]; while (left < right) { int sum = nums[left] + nums[right]; if (sum > target) { --right; } else if (sum < target) { ++left; } else { // 将获取的三元组尾插ret里 ret.push_back({nums[i], nums[left], nums[right]}); // 将所有的情况获取--不漏，并去重 // 缩小区间查找 ++left; --right; // 去重left和right，注意区间越界问题 while (left < right && nums[left] == nums[left - 1]) { ++left; } while (left < right && nums[right] == nums[right + 1]) { --right; } } } // 注意去重i ++i; while (i < n && nums[i] == nums[i - 1]) { ++i; } } return ret; }};注：这里时间复杂度是O（N²）。
提交记录：
制作不易,若有不足之处或出问题的地方，请各位大佬多多指教 ，感谢大家的阅读支持！！!
