目录
一、常见进制介绍
1.1 十进制(Decimal)
1.2. 二进制(Binary)
1.3. 八进制(Octal)
1.4. 十六进制(Hexadecimal)
二、进制转换方法
2.1. 二进制与十进制之间的转换
2.2. 八进制与十进制之间的转换
2.3. 十六进制与十进制之间的转换
2.4. 二进制、八进制与十六进制之间的转换
三、进制转换在嵌入式开发中的应用
3.1. 数据存储
3.2. 数据传输
3.3. 代码优化
3.4. 其他应用
3.5. 示例代码
四、注意事项
4.1. 精度问题
4.2. 转换工具
4.3. 边界条件处理
4.4. 性能优化
4.5. 代码可读性
五、总结
在嵌入式开发领域,进制转换是一项基础且至关重要的技能。计算机内部采用二进制进行数据存储和运算,而开发者通常使用十进制、八进制或十六进制来表示和操作数据。因此,掌握进制转换对于理解和优化嵌入式系统至关重要。
一、常见进制介绍
进制是计算技术中用于表示数值的一种方式,不同的进制使用不同数量的符号来表示数值。
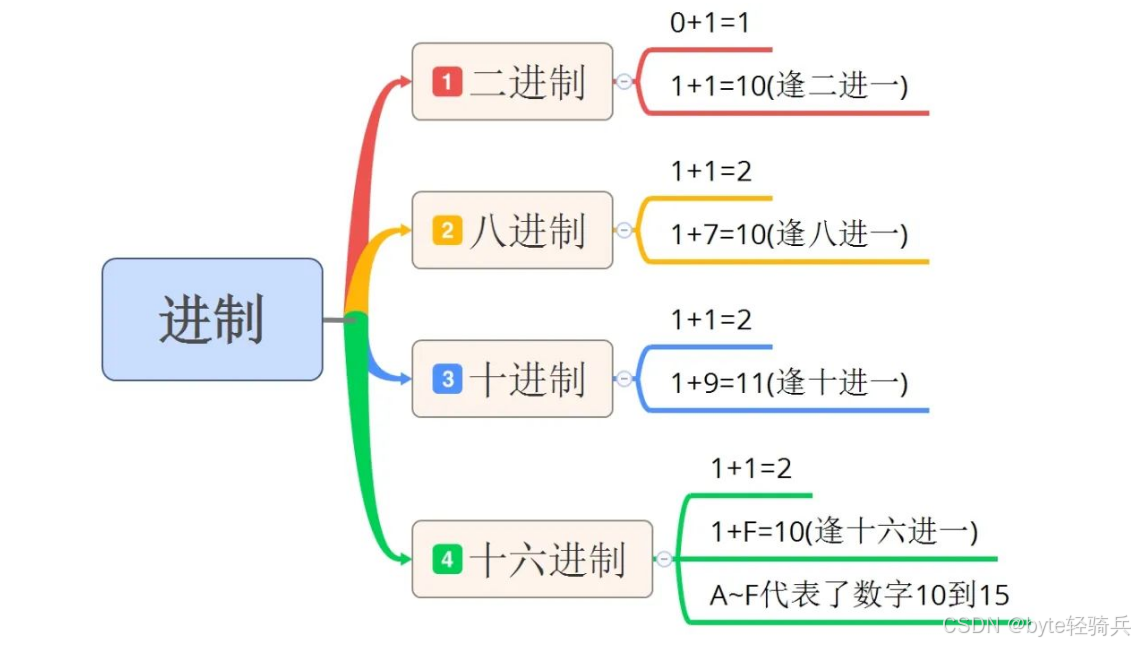
常见进制包括二进制(0和1)、八进制(0-7)、十六进制(0-9及A-F)和十进制(0-9),它们在计算机科学、数学和其他领域中有着广泛的应用。了解这些进制的特点和转换方法对于理解计算机的工作原理和进行数值计算都是非常重要的。
1.1 十进制(Decimal)
1.2. 二进制(Binary)

1.3. 八进制(Octal)

1.4. 十六进制(Hexadecimal)

二、进制转换方法
2.1. 二进制与十进制之间的转换
二进制转十进制:二进制数由0和1组成,每一位的数值是其位置上的权值(2的幂次方)乘以该位上的数字(0或1)。将所有这些乘积相加,即可得到十进制数。例如:二进制数 1101 转换为十进制数的计算过程为:1×2^3 + 1×2^2 + 0×2^1 + 1×2^0 = 8 + 4 + 0 + 1 = 13
23 转换为二进制数的过程为:23 ÷ 2 = 11 余 111 ÷ 2 = 5 余 15 ÷ 2 = 2 余 12 ÷ 2 = 1 余 01 ÷ 2 = 0 余 1从下往上读取余数,得到
23 的二进制表示为 10111。 2.2. 八进制与十进制之间的转换
八进制转十进制:八进制数由0到7的数字组成,每一位的数值是其位置上的权值(8的幂次方)乘以该位上的数字。将所有这些乘积相加,即可得到十进制数。 例如: 八进制数7654 转换为十进制数的计算过程为:7×8^3 + 6×8^2 + 5×8^1 + 4×8^0 = 28672 + 3072 + 400 + 4 = 32148十进制转八进制:将十进制数不断除以8,记录余数,直到商为0。将余数按从低位到高位的顺序排列,得到的数就是对应的八进制数。 例如:将十进制数29转换为八进制的过程为: 29 ÷ 8 = 3 余 5
所以 29 的八进制表示为 35。
2.3. 十六进制与十进制之间的转换
十六进制转十进制:十六进制数由0到9和A到F(或a到f)组成,其中A到F代表10到15。每一位的数值是其位置上的权值(16的幂次方)乘以该位上的数字(0-9或A-F)。将所有这些乘积相加,即可得到十进制数。例如:十六进制数 3E 转换为十进制数的计算过程为:3×16^1 + 14×16^0 = 48 + 14 = 62
123 转换为十六进制数的过程为: 123 ÷ 16 = 7 余 11(B)7 ÷ 16 = 0 余 7
所以 123 的十六进制表示为 7B。
2.4. 二进制、八进制与十六进制之间的转换
二进制转八进制:从小数点开始,分别向左、右按3位分组转换成对应的八进制数字字符,最后不满3位的,则需补0。 例如,二进制数 110101 转换为八进制。 分组为 011 和 010 和 101。011 对应八进制数 3,010 对应八进制数 2,101 对应八进制数 5。所以,110101 的八进制表示为 65。八进制转二进制:将每位八进制数用3位二进制数表示即可。例如:八进制数 35 转换为二进制:3 转换为二进制为 0115 转换为二进制为 101
所以 35 的二进制表示为 011101(注意:通常我们省略前导的0,但在这里为了保持位数一致,我保留了它)。
110101 转换为十六进制: 分组为 0011 和 0101(注意:这里我添加了前导的0以保持4位一组)。0011 对应十六进制数 3,0101 对应十六进制数 5。
所以 110101 的十六进制表示为 35。
35 转换为二进制:3 转换为二进制为 00115 转换为二进制为 0101所以
35 的二进制表示为 00110101(同样,为了保持位数一致,我保留了前导的0,但在实际应用中通常会省略它们)。 三、进制转换在嵌入式开发中的应用
进制转换在嵌入式开发中具有广泛的应用,不仅涉及数据存储、数据传输,还与代码优化等多个方面紧密相连。
3.1. 数据存储
在嵌入式系统中,数据通常以二进制形式存储在内存中。了解进制转换有助于开发者理解数据的存储方式,并进行有效的数据读写操作。
二进制存储的优势:计算机系统是基于二进制运算的,使用二进制可以直接与硬件交互,减少中间步骤,提高存储和读取的速度。因此,在存储器中,数据以二进制的形式存储,数据的读取和写入都非常快速。不同进制的优化存储:虽然二进制是最基础的进制,但在某些情况下,使用其他进制(如十六进制)可以优化存储空间。例如,十六进制是二进制的简化表示形式,每个十六进制字符可以表示四个二进制位,这使得数据表示更加紧凑。3.2. 数据传输
在嵌入式系统中,数据常常需要在不同的模块或设备之间进行传输。了解进制转换有助于开发者设计高效的数据传输协议,并确保数据的正确传输。具体来说:
进制转换与数据传输效率:通过选择合适的进制表示方式,可以优化数据传输的效率。例如,十六进制编码常用于网络数据包的表示和传输,因为它可以将二进制数据表示得更加紧凑,减少传输的字符数量。数据安全性:在加密通信中,不同的进制表示可以用于加密算法和密钥的生成与传输。通过使用不同的进制,可以提高加密算法的复杂性和安全性,从而保护数据免受未授权访问。3.3. 代码优化
在嵌入式开发中,代码的优化对于提高系统的性能和降低功耗至关重要。了解进制转换有助于开发者编写更加紧凑和高效的代码,减少不必要的资源消耗。具体来说:
减少代码量:通过合理使用进制转换,可以减少代码中的冗余部分,使代码更加简洁明了。例如,在处理二进制数据时,可以直接使用位操作来替代复杂的算术运算,从而减少代码量并提高执行效率。优化数据结构:在选择数据结构时,可以考虑数据的存储和访问方式。通过选择合适的进制表示方式,可以优化数据结构的存储和访问效率。例如,在嵌入式系统中常用的链表、数组等数据结构,可以通过优化数据的存储顺序和访问方式来提高性能。3.4. 其他应用
除了上述三个方面外,进制转换在嵌入式开发中还有其他重要的应用:
硬件编程与低级系统操作:在硬件编程和低级系统操作中,十六进制与二进制的转换非常常见。开发者需要熟悉这些进制之间的转换规则,以便能够正确地与硬件进行交互。硬件配置:在配置寄存器时,常常需要使用十六进制或二进制来设置特定的位。例如,设置一个 GPIO 引脚的输入输出模式,可能需要通过写入特定的十六进制值到寄存器中来实现。调试与开发:在调试和开发过程中,使用十六进制表示数据可以方便地查看内存和数据结构的内容。这是因为十六进制比二进制更加简洁,同时比十进制更能直观地反映数据的二进制结构。进制转换在嵌入式开发中具有广泛的应用和重要的作用。开发者需要熟练掌握进制转换的基本知识和技巧,以便能够更好地理解和处理嵌入式系统中的数据、代码和硬件交互问题。
3.5. 示例代码
以下是一个C语言代码示例,展示进制转换在嵌入式开发中的一些基本应用。请注意,这个示例主要是为了教学目的,实际应用中可能需要更复杂的处理和优化。
#include <stdio.h>#include <stdint.h>// 将二进制字符串转换为十进制整数uint32_t binaryToDecimal(const char *binaryStr) { uint32_t decimal = 0; while (*binaryStr) { decimal = decimal * 2 + (*binaryStr - '0'); binaryStr++; } return decimal;}// 将十进制整数转换为二进制字符串(静态分配缓冲区,注意溢出风险)void decimalToBinary(uint32_t decimal, char *binaryStr, size_t bufferSize) { binaryStr[bufferSize - 1] = '\0'; // 确保字符串以null结尾 for (size_t i = bufferSize - 2; i >= 0; i--) { binaryStr[i] = (decimal % 2) ? '1' : '0'; decimal /= 2; } // 移除前导零(除了最高位可能是0的情况) char *start = binaryStr; while (*start == '0' && *(start + 1) != '\0') { start++; } if (*start == '\0') { // 如果整个字符串都是0 binaryStr[0] = '0'; } else { // 将非零部分复制到缓冲区开头 for (size_t j = 0; j < bufferSize - (start - binaryStr) - 1; j++) { binaryStr[j] = start[j]; } binaryStr[bufferSize - (start - binaryStr) - 1] = '\0'; } // 注意:这里为了简化,没有处理缓冲区溢出的情况。在实际应用中,应该添加额外的检查。}// 将十六进制字符串转换为十进制整数uint32_t hexToDecimal(const char *hexStr) { uint32_t decimal = 0; while (*hexStr) { char ch = *hexStr; if (ch >= '0' && ch <= '9') { decimal = decimal * 16 + (ch - '0'); } else if (ch >= 'A' && ch <= 'F') { decimal = decimal * 16 + (ch - 'A' + 10); } else if (ch >= 'a' && ch <= 'f') { decimal = decimal * 16 + (ch - 'a' + 10); } hexStr++; } return decimal;}// 将十进制整数转换为十六进制字符串(静态分配缓冲区,注意溢出风险)void decimalToHex(uint32_t decimal, char *hexStr, size_t bufferSize) { static const char hexDigits[] = "0123456789ABCDEF"; hexStr[bufferSize - 1] = '\0'; // 确保字符串以null结尾 for (size_t i = bufferSize - 2; i >= 0; i--) { hexStr[i] = hexDigits[decimal % 16]; decimal /= 16; } // 反转字符串,因为我们是从后往前填充的 for (size_t j = 0; j < bufferSize / 2; j++) { char temp = hexStr[j]; hexStr[j] = hexStr[bufferSize - j - 2]; hexStr[bufferSize - j - 2] = temp; } // 如果最高位是0(即整个数都是0或者小于16),则需要在前面补0 if (hexStr[0] == '\0') { hexStr[0] = '0'; } // 注意:同样没有处理缓冲区溢出的情况。}int main() { // 示例使用 const char *binaryStr = "1101"; uint32_t decimal = binaryToDecimal(binaryStr); printf("Binary %s to Decimal: %u\n", binaryStr, decimal); char binaryBuffer[33]; // 32位二进制数 + null终止符 decimalToBinary(decimal, binaryBuffer, sizeof(binaryBuffer)); printf("Decimal %u to Binary: %s\n", decimal, binaryBuffer); const char *hexStr = "1A3F"; decimal = hexToDecimal(hexStr); printf("Hex %s to Decimal: %u\n", hexStr, decimal); char hexBuffer[9]; // 8位十六进制数 + null终止符 decimalToHex(decimal, hexBuffer, sizeof(hexBuffer)); printf("Decimal %u to Hex: %s\n", decimal, hexBuffer); return 0;}在这个示例中,我们定义了四个函数来进行二进制、十进制和十六进制之间的转换。binaryToDecimal 函数将二进制字符串转换为十进制整数,decimalToBinary 函数将十进制整数转换为二进制字符串(注意,这里为了简化,使用了静态分配的缓冲区,并且没有处理所有可能的边界情况)。hexToDecimal 函数将十六进制字符串转换为十进制整数,而 decimalToHex 函数则将十进制整数转换为十六进制字符串。
在 main 函数中,我们展示了如何使用这些函数进行进制转换,并打印出结果。
请注意,这个示例中的 decimalToBinary 和 decimalToHex 函数没有处理所有可能的边界情况,特别是当转换结果需要比提供的缓冲区更大时。在实际应用中,应该添加额外的检查来确保不会发生缓冲区溢出。此外,对于嵌入式系统,可能还需要考虑内存使用和性能优化。
四、注意事项
在嵌入式开发中进行进制转换时,需要注意以下几点。
4.1. 精度问题
在进行进制转换时,特别是从高精度进制(如十进制)转换到低精度进制(如二进制或十六进制)时,可能会遇到无法完全表示原始数值的情况,从而导致精度丢失。然而,在二进制、八进制、十六进制和十进制这些常用进制之间转换时,只要目标进制能够表示源进制的所有值,就不会发生精度丢失(例如,32位二进制数可以无损转换为十进制数,只要十进制数的表示范围足够大)。需要特别注意的是,当使用浮点数进行进制转换时,由于浮点数的表示方式(如IEEE 754标准)本身存在精度限制,因此可能会遇到精度问题。在进行浮点数转换时,应该使用适当的库函数或算法来确保精度尽可能高。4.2. 转换工具
在实际开发中,使用专业的进制转换工具可以大大提高开发效率。这些工具通常提供了用户友好的界面,可以方便地进行各种进制之间的转换,并且支持大数值的处理。除了专门的进制转换软件外,还可以使用编程语言中的内置函数或库来进行进制转换。例如,C语言中的printf和scanf函数可以通过格式说明符来指定输出或输入的进制。 4.3. 边界条件处理
在进行进制转换时,需要特别注意边界条件的处理。例如,当转换的结果超出目标类型的表示范围时,应该采取适当的措施(如溢出检测、错误报告等)来避免数据损坏或程序崩溃。此外,还需要注意处理空字符串、非法字符等异常情况,以确保转换过程的健壮性。4.4. 性能优化
在嵌入式开发中,性能优化通常是一个重要的考虑因素。因此,在进行进制转换时,需要权衡转换算法的时间复杂度和空间复杂度,选择最适合当前应用场景的算法。例如,在处理大量数据时,可以使用位操作等高效算法来减少转换时间;在内存资源有限的情况下,可以优化数据结构以减少存储空间的使用。4.5. 代码可读性
在编写进制转换代码时,需要注重代码的可读性和可维护性。这包括使用清晰的变量命名、合理的函数划分、适当的注释等。通过编写易于理解的代码,可以降低后续维护和调试的难度,提高开发效率。在进行进制转换时,需要注意精度问题、选择合适的转换工具、妥善处理边界条件、进行性能优化以及注重代码可读性等方面的问题。这些注意事项有助于确保转换过程的准确性和高效性,从而提高嵌入式系统的整体性能和可靠性。
五、总结
进制转换在嵌入式开发中扮演着基础且至关重要的角色。它不仅是理解计算机内部工作原理的关键,也是优化嵌入式系统性能、提高开发效率的重要手段。
基础理解:进制转换是计算机科学和嵌入式开发的基石。理解不同进制(如二进制、八进制、十六进制和十进制)之间的转换关系,有助于开发者更深入地理解计算机内部的数据表示和处理方式。系统优化:在嵌入式开发中,进制转换常用于优化系统性能。例如,通过选择合适的进制表示数据,可以减少存储空间的占用,提高数据处理的效率。此外,了解计算机内部的二进制运算机制,有助于开发者编写出更高效、更紧凑的代码。调试与诊断:进制转换在调试和诊断嵌入式系统时发挥着重要作用。通过查看和分析系统内部的二进制数据,开发者可以定位并解决程序中的错误和异常。此外,使用十六进制等进制表示内存地址和数据,可以更方便地进行内存访问和数据分析。跨平台兼容性:在嵌入式开发中,不同平台和设备可能使用不同的数据表示方式和进制。掌握进制转换技能,有助于开发者在跨平台开发时确保数据的正确性和兼容性。持续学习与提升:进制转换是一个不断发展的领域。随着计算机技术的不断进步和嵌入式系统的广泛应用,新的进制转换方法和工具不断涌现。因此,开发者需要保持持续学习的态度,不断更新自己的知识和技能,以适应不断变化的市场需求和技术趋势。团队协作与沟通:在嵌入式开发团队中,掌握进制转换技能有助于团队成员之间的沟通和协作。通过使用统一的进制表示和转换方法,可以减少误解和错误,提高团队的整体开发效率。综上所述,进制转换在嵌入式开发中具有重要的地位和作用。掌握进制转换的基本概念和方法,不仅有助于开发者更好地理解和优化嵌入式系统,还能提高开发效率和系统性能。因此,对于嵌入式开发者来说,深入学习和掌握进制转换技能是必不可少的。