概述
1.邻接表的优缺点
邻接表是一种表示图的数据结构,事实上邻接表可以用于有向图、无向图、带权图、无权图。
邻接表表示法的优点主要有空间效率、遍历效率
空间利用率高:邻接表相较于邻接矩阵更加节省空间,特别是对于稀疏图。因为邻接表只需要储存实际存在的边,而邻接矩阵需要储存所有的边。遍历速度:邻接表在遍历与某顶点相邻的全部顶点时,时间复杂度与顶点的度成正比。对于稀疏图而言,这比邻接矩阵表示法的时间复杂度要低。邻接表的缺点
不适合储存稠密图,此时邻接表顶点的边列表过长,导致储存和访问的效率大大降低。代码复杂,相较于邻接矩阵,邻接表表示法的代码逻辑稍复杂。2.怎么从树->图(一对多->多对多)
今天我们用链表形式来实现一个邻接表,在实现邻接表之前,我们先观察一张有向图来摸索一下图中结点之间的关系:
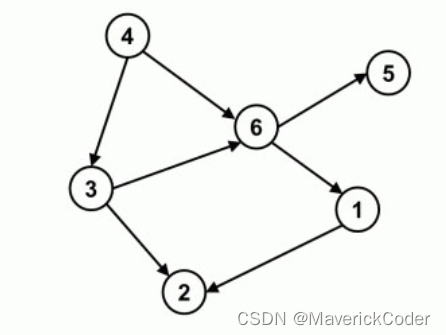
很自然地,我们会将这张有向图拆成两个部分:连接两个结点的有向边以及每个结点。
那么我们应该如何用链表将这些信息储存起来呢?让我们回想一下树是如何用链表实现的,我们用数组TreeNode *nodes来储存结点,然后通过TreeNode* node->childrenlist(子结点链表)来记录每个结点下的子结点,这就是树结构(一对多)用链表的实现。
然后我们思考如何将这种树结构通过变换,来达到多对多的目的。我们首先明确一条边只能连接两个结点(这是关键),然后想着为结点、有向边定义两种结构体(VertexNode、EdgeNode)。在图结点结构体中要有一个链表(EdgeNode* firstEdge)储存所有由该结点发出的边,还要有数据域。每个边结构体中存放指向的顶点数据,如此就能够将有向图的数据结构用链表表达出来。

1.邻接表的结构体申明
首先是必要的头文件:
#include <stdio.h>#include <stdlib.h>然后我们根据先前的分析定义三个结构体用于图的数据结构:
EdgeNode结构体用于表示图中的边,包括三个成员,vertex(这条边指向的顶点)、weight(这条边的权重)、*next(用于指向下一个边结点)VertexNode结构体用于表示图中的顶点,包括两个成员,vertex(顶点索引)、firstEdge(指向该结点的第一个边结点)Graph结构体用于整个图的表示,包括两个成员,vertices(顶点的数量)、数组nodes(用于记录所有顶点信息)typedef struct EdgeNode {int vertex; //这条边的结尾顶点 int weight; //这条边上的权重 struct EdgeNode* next; //指向下一边结点} EdgeNode; typedef struct VertexNode {int vertex; //顶点数据域 EdgeNode* firstEdge; //指向该顶点的第一条边 } VertexNode; typedef struct Graph {int vertices; //顶点的数量 VertexNode* nodes; //用来记录每个顶点信息 } Graph; 2.邻接表的创建
邻接表的创建就是将其初始化,调用malloc函数将g->nodes的空间分配好后,然后每个顶点赋值编号,并且将每个顶点指向的第一条边置空:
void GraphCreat(Graph* g,int vertices) { //传入的参数是表*g和结点的数量vertices g->vertices=vertices; g->nodes=(VertexNode*)malloc(sizeof(VertexNode)*vertices);//为g->nodes分配空间 for(int i=0;i<g->vertices;i++){ g->nodes[i].vertex=i; //将每个结点的数据初始化为结点编号g->nodes[i].firstEdge=NULL; //且将结点指向的第一条边置空 }}3.邻接表的销毁
销毁时需要将每个顶点的空间释放掉,仅需要获取每个顶点邻接边的链表头,然后遍历做删除操作即可:
void GraphDestroy(Graph* g) {for(int i=0;i<g->vertices;i++){EdgeNode* cur=g->nodes[i].firstEdge;while(cur){EdgeNode* temp=cur;cur=cur->next;free(temp);}}free(g->nodes);g->nodes=NULL;}4.邻接表的边添加
操作结果是是添加一条u->v,权值为w的有向边,需要新定义一个边结点,将v作为该边结尾的顶点,w赋给该有向边的权值。然后将新边结点的后继next指向第u号元素的链表头,最后将链表头更新为新的边结点:
void GraphAddEdge(Graph* g,int u,int v,int w) {EdgeNode* nownode=(EdgeNode*)malloc(sizeof(EdgeNode));nownode->vertex=v;nownode->weight=w;nownode->next=g->nodes[u].firstEdge; //典型的头插法 g->nodes[u].firstEdge=nownode; } 5.邻接表的打印
void GraphPrint(Graph* g) {for(int i=0;i<g->vertices;i++){EdgeNode* cur=g->nodes[i].firstEdge;printf("Vertex %d:",i);while(cur){printf("%d(%d)",cur->vertex,cur->weight);cur=cur->next;}printf("\n");} } 打印就是将该图遍历一遍,并且将顶点值与该顶点的边结点(包括边结尾顶点值)及权重依次打印出来。
例如下面有向图:
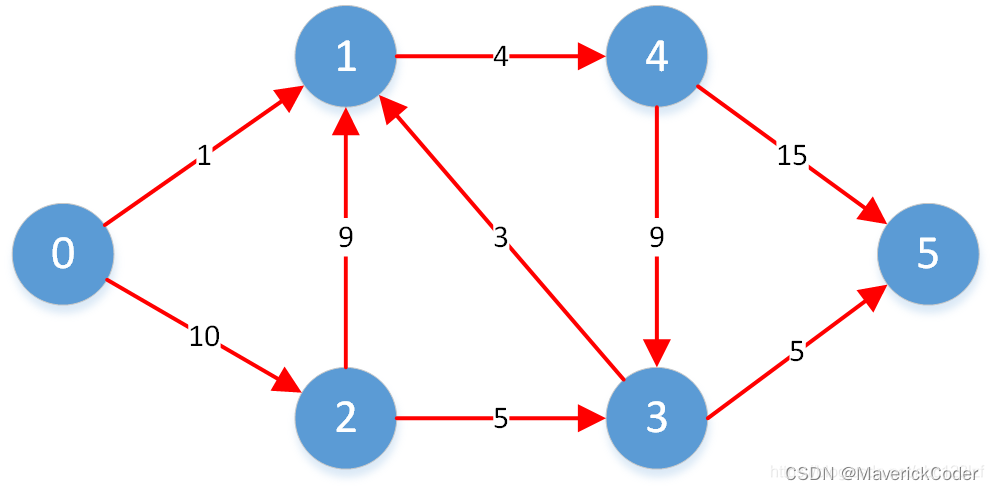
打印的结果应该为:

完整源码
#include <stdio.h>#include <stdlib.h>typedef struct EdgeNode {int vertex; //这条边的结尾顶点 int weight; //这条边上的权重 struct EdgeNode* next; //指向下一条边 } EdgeNode; typedef struct VertexNode {int vertex; //顶点数据域 EdgeNode* firstEdge; //指向该节点的第一条边 } VertexNode; typedef struct Graph {int vertices; //结点的数量 VertexNode* nodes; //用来记录每个结点 } Graph; void GraphCreat(Graph* g,int vertices) { //传入的参数是表g和结点的数量vertices g->vertices=vertices; g->nodes=(VertexNode*)malloc(sizeof(VertexNode)*vertices);//为g->node分配空间 for(int i=0;i<g->vertices;i++){ g->nodes[i].vertex=i; //将每个结点的数据初始化为结点编号g->nodes[i].firstEdge=NULL; //且将结点指向的第一条边置空 }}void GraphDestroy(Graph* g) {for(int i=0;i<g->vertices;i++){EdgeNode* cur=g->nodes[i].firstEdge;while(cur){EdgeNode* temp=cur;cur=cur->next;free(temp);}}free(g->nodes);g->nodes=NULL;}void GraphAddEdge(Graph* g,int u,int v,int w) {EdgeNode* nownode=(EdgeNode*)malloc(sizeof(EdgeNode));nownode->vertex=v;nownode->weight=w;nownode->next=g->nodes[u].firstEdge; //典型的头插法 g->nodes[u].firstEdge=nownode; } void GraphPrint(Graph* g) {for(int i=0;i<g->vertices;i++){EdgeNode* cur=g->nodes[i].firstEdge;printf("Vertex %d:",i);while(cur){printf("%d(%d)",cur->vertex,cur->weight);cur=cur->next;}printf("\n");} } int main (){Graph g;GraphCreat(&g,5);GraphAddEdge(&g,0,1,4);GraphAddEdge(&g,0,2,2);GraphAddEdge(&g,1,2,3);GraphAddEdge(&g,2,3,4);GraphAddEdge(&g,3,4,2);GraphPrint(&g);GraphDestroy(&g);return 0; }