题面:
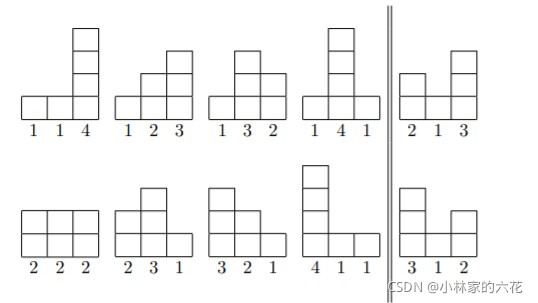
Miguel Angelo is a great sculptor, widely recognized for his outdoor sculptures. In his hometown, it is very common to find one of his creations in squares and gardens. People love his sculptures, not only for their beauty, but also because they look like new even after decades. The sculptures do not degrade easily due to the material and technique developed by Miguel and his staff over the years. To build the sculptures, he first constructs its base by stacking blocks of waterproof plaster (his secret material), forming several stacks of blocks in a straight line. He always uses identical blocks, and each stack has at least one block. To stabilize the structure, he surrounds it by two big glass panes, one behind the stacks and one in front of them. Then he waits for the rain for as long as it takes. If the structure is such that it doesn’t accumulate water during this procedure, Miguel is sure that the base can be used to obtain a piece of long-lasting artwork. Notice that water will accumulate on a block if there are obstacles (other blocks) on both sides (to the left and to the right). The following picture shows the front view of several different bases. All of them consist of three stacks made of a total of six blocks, with each stack having at least one block as required. However, the eight bases on the left will lead to long-lasting artwork, while the two bases on the right will not.
Miguel Angelo is receiving a lot of sculpture requests. Although he has all the freedom to create the artwork, he wants to be fair and use the same number of stacks and the same number blocks in each of the sculptures. Since he doesn’t want to sell identical sculptures to different clients, he will construct a different base each time. He worries that he won’t be able to fulfill all the requests. Help him calculate the number of different bases given the number of stacks and the number of blocks that the base must have.
Input
The input consists of a single line that contains two integers S and B (1 ≤ S ≤ B ≤ 5000) indicating respectively the number of stacks and the number of blocks that the base must have.
Output
Output a single line with an integer indicating the number of different bases that don’t accumulate water which Miguel can construct. Because this number can be very large, output the remainder of dividing it by 109 + 7.
Sample input
3 6
Sample output
8
Sample input
3 7
Sample output
12
题意:
大致就是给了 B 个积木,底部放置 S 个积木,求剩余积木在底座上摆放并且不产生凹槽摆放的组合数量。
思路:
在刚开始我排除了 dp (因为我真的太菜了,找不到状态,以为只是容斥就能做的,ca),事后补题后发现是一个 dp 题,并且需要维护。
首先考虑定义状态,这个状态由于经过前缀和的维护,不是直接递推出来的,所以比较难想象状态。
仔细考虑一下,题目要求的是底座为 S ,上边防止 S - B 个数量的积木并且不组成凹槽的摆放组合数量。其实整体无论摆了几层,去掉最后一层,上边仍旧满足着不存在凹槽。所以上一层便是一个底座为 x(1 <= x <= S),上次 S - B -x 的数量的积木摆放不组成凹槽的个数。
所以可以设定为dp [ i ][ j ]的状态为 最下层为 i ,上层摆放 j 个积木并且不组成凹槽的数量。由于每次底座上方的次层数量不固定,摆放方式也不固定,例如 S 的底座上方一个积木有 S个摆放方法,所以可以得到如下的 dp 转移方程:
dp[ i ][ j ] = dp[ 1 ][ j - 1] * i + dp[ 2 ][ j - 2 ] * ( i - 1 ) + ··· + dp[ i ][ j - i ] * ( i - j ) ( j >= i )
dp[ i ][ j ] = dp[ 1 ][ j - 1] * i + dp[ 2 ][ j - 2 ] * ( i - 1 ) + ··· + dp[ j ][ 0 ] * ( i - j ) (j < i)
推出来转移方程后,发现这是一个三维的循环,再瞪眼看一下数据量,emmmm,铁超时。于是可以每求出一个dp[ i ][ j ]之后,将其的数值加到累加和中去,通过每一轮前缀和,减少第三轮的循环,从而得出两重循环的结果。
而累加和的存在,也需要我们建立一个合适的sum数组,很显然,每一次dp数组所需的元素都具有一个相同的因素,那便是 i + j 的值相同,所以我们便可以根据这个值来设立前缀和数组,即上方总共为( i + j )个积木的组成数量,因为后边需要乘数,但是每个乘数也是与 i 紧紧相关联的,于是每次经过一次 j 层的循环,我们可以加上上次dp数组提供的贡献,便构成了一直滚动的前缀和。
由于每一轮dp数组都会对不同的i + j提供贡献,所以我们需要记录所有的总贡献数量,利用pre数组定义为前边总共 i + j 个积木的总贡献,再加上sum数组的贡献,便是 j 个积木在底座 i 上的贡献。
首先我们也需要考虑dp数组以及sum数组的初始化,很显然,当j=0时,dp[ i ][ j ]的值显然为1,此时sum数组也应该不断更新。
代码:
#include <bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f;
const int maxn=5e3+5;
const int mod=1e9+7;
int sum[maxn*2],dp[maxn][maxn],pre[maxn*2];
int main()
{
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int s,b;cin>>s>>b;
b-=s;
for(int i=1;i<=s;i++){
for(int j=0;j<=b;j++){
sum[j]=(sum[j]+pre[j])%mod;
if(j==0)dp[i][j]=1;
else {
dp[i][j]=(dp[i][j]+sum[j])%mod;
}
pre[i+j]=(pre[i+j]+dp[i][j])%mod;
}
}
cout<<dp[s][b]<<endl;
return 0;
}
/*
3 6
3 7
*/
参考:Gym102428F Fabricating Sculptures {DP}【线性DP】(前缀和)_Hc_Soap的博客-CSDN博客qGym102428F Fabricating Sculptures(DP+前缀和)DescriptionMiguel Angelo is a great sculptor, widely recognized for his outdoor sculptures. In his hometown, it is very common to find one of his creations in squares and gardens. People love his sculptures, not ohttps://blog.csdn.net/Hc_Soap/article/details/108984133?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522163206830216780255255835%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=163206830216780255255835&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-3-108984133.first_rank_v2_pc_rank_v29&utm_term=F+-+Fabricating+Sculptures+Gym+-+102428F+&spm=1018.2226.3001.4187
侵删。