目录
- G711简介
- G711A
- 算法原理
- 压缩方法
- 举例
- 代码
- G711U
- 算法原理
- 压缩方法
- 举例
- 代码
- G711A与G711U对比
参考链接
G711简介
G711是国际电信联盟ITU-T定制出来的一套语音压缩标准,它代表了对数PCM(logarithmic pulse-code modulation)抽样标准,主要用于电话。它主要用脉冲编码调制对音频采样,采样率为8k每秒。它利用一个 64Kbps 未压缩通道传输语音讯号。 起压缩率为1:2, 即把16位数据压缩成8位。G.711是主流的波形声音编解码器。
G.711 标准下主要有两种压缩算法。一种是u-law algorithm (又称often u-law, ulaw, mu-law),主要运用于北美和日本;另一种是A-law algorithm,主要运用于欧洲和世界其他地区。其中,后者是特别设计用来方便计算机处理的
G711的内容是将14bit(uLaw)或者13bit(aLaw)采样的PCM数据编码成8bit的数据流,播放的时候在将此8bit的数据还原成14bit或者13bit进行播放,不同于MPEG这种对于整体或者一段数据进行考虑再进行编解码的做法,G711是波形编解码算法,就是一个sample对应一个编码,所以压缩比固定为:
-
8/14 = 57% (uLaw)
-
8/13 = 62% (aLaw)
简单理解,G.711就是语音模拟信号的一种非线性量化, bitrate 是64kbps,sample rate是8K,压缩率固定为2.
G711A
算法原理
A-law的公式如下,一般采用A=87.6
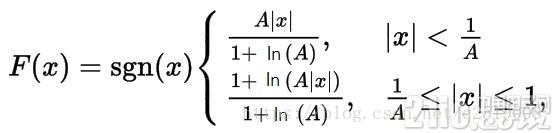
画出图来则是如下图,用x表示输入的采样值,F(x)表示通过A-law变换后的采样值,y是对F(x)进行量化后的采样值。
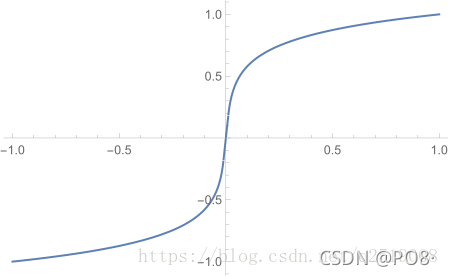
由此可见在输入的x为高值的时候,F(x)的变化是缓慢的,有较大范围的x对应的F(x)最终被量化为同一个y,精度较低。相反在低声强区域,也就是x为低值的时候,F(x)的变化很剧烈,有较少的不同x对应的F(x)被量化为同一个y。意思就是说在声音比较小的区域,精度较高,便于区分,而声音比较大的区域,精度不是那么高。
这也体现了G711的应用场景——话机通话
对应解码公式(即上面函数的反函数):
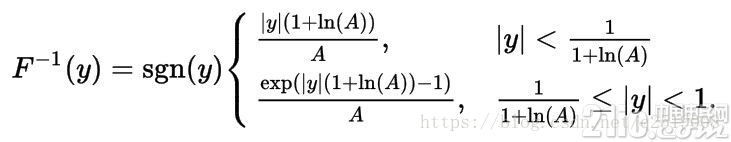
压缩方法
G711A(A-LAW)压缩十三折线法
g711a输入的是13位(S16的高13位),这种格式是经过特别设计的,便于数字设备进行快速运算。
- 1、取符号位并取反得到s
- 2、获取强度位eee,获取方法如图所示
- 3、获取高位样本位wxyz
- 4、组合为seeewxyz,将seeewxyz逢偶数为取补数,编码完毕
A-law如下表计算,第一列是采样点,共13bit,最高位为符号位。对于前两行,折线斜率均为1/2,跟负半段的相应区域位于同一段折线上,对于3到8行,斜率分别是1/4到1/128,共6段折线,加上负半段对应的6段折线,总共13段折线,这就是所谓的A-law十三段折线法。
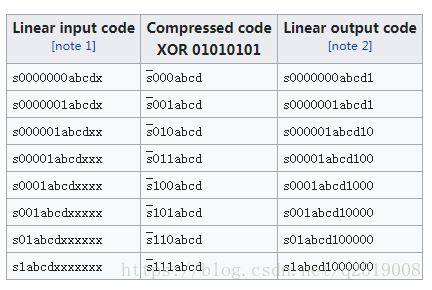
举例
已知G711是将S16压缩为S8,于是输入必是S16
假设输入PCM数据为0x1234,即0b0000 0100 1101 0010
由于是signed,所以可以表示为0b 0 00001 0011 010010
查表可得:
- 1、符号位为0,取反
s = 1 - 2、获取强度位00001,查表得知,编码
eee = 011 - 3、最高位样本
wxyz = 0011 - 4、组合起来为
0b1011 0011,逢偶数位取反为0b1110 0110,即为0xE6
代码
#define SIGN_BIT (0x80) /* Sign bit for a A-law byte. */
#define QUANT_MASK (0xf) /* Quantization field mask. */
#define NSEGS (8) /* Number of A-law segments. */
#define SEG_SHIFT (4) /* Left shift for segment number. */
#define SEG_MASK (0x70) /* Segment field mask. */
static int seg_aend[8] = {0x1F, 0x3F, 0x7F, 0xFF,
0x1FF, 0x3FF, 0x7FF, 0xFFF};
static int seg_uend[8] = {0x3F, 0x7F, 0xFF, 0x1FF,
0x3FF, 0x7FF, 0xFFF, 0x1FFF};
static int search(
int val, /* changed from "short" *drago* */
int *table,
int size) /* changed from "short" *drago* */
{
int i; /* changed from "short" *drago* */
for (i = 0; i < size; i++) {
if (val <= *table++)
return (i);
}
return (size);
}
int linear2alaw(int pcm_val) /* 2's complement (16-bit range) */
/* changed from "short" *drago* */
{
int mask; /* changed from "short" *drago* */
int seg; /* changed from "short" *drago* */
int aval;
pcm_val = pcm_val >> 3;//这里右移3位,因为采样值是16bit,而A-law是13bit,存储在高13位上,低3位被舍弃
if (pcm_val >= 0) {
mask = 0xD5; /* sign (7th) bit = 1 二进制的11010101*/
} else {
mask = 0x55; /* sign bit = 0 二进制的01010101*/
pcm_val = -pcm_val - 1; //负数转换为正数计算
}
/* Convert the scaled magnitude to segment number. */
seg = search(pcm_val, seg_aend, 8); //查找采样值对应哪一段折线
/* Combine the sign, segment, and quantization bits. */
if (seg >= 8) /* out of range, return maximum value. */
return (0x7F ^ mask);
else {
//以下按照表格第一二列进行处理,低4位是数据,5~7位是指数,最高位是符号
aval = seg << SEG_SHIFT;
if (seg < 2)
aval |= (pcm_val >> 1) & QUANT_MASK;
else
aval |= (pcm_val >> seg) & QUANT_MASK;
return (aval ^ mask);
}
}
int alaw2linear(int a_val)
{
int t; /* changed from "short" *drago* */
int seg; /* changed from "short" *drago* */
a_val ^= 0x55; //异或操作把mask还原
t = (a_val & QUANT_MASK) << 4;//取低4位,即表中的abcd值,然后左移4位变成abcd0000
seg = ((unsigned)a_val & SEG_MASK) >> SEG_SHIFT; //取中间3位,指数部分
switch (seg) {
case 0: //表中第一行,abcd0000 -> abcd1000
t += 8;
break;
case 1: //表中第二行,abcd0000 -> 1abcd1000
t += 0x108;
break;
default://表中其他行,abcd0000 -> 1abcd1000 的基础上继续左移(按照表格第二三列进行处理)
t += 0x108;
t <<= seg - 1;
}
return ((a_val & SIGN_BIT) ? t : -t);
}
G711U
u-law也叫g711u,使用在北美和日本,输入的是14位,编码算法就是查表,计算出:基础值+平均偏移值 没啥复杂算法,就是基础值+平均偏移值,
算法原理
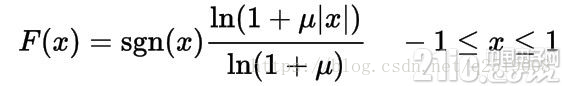
压缩方法
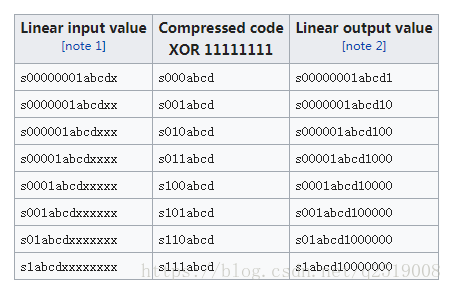
相应的μ-law的计算方法如下表
此为查表法

举例
此为代码采用的算法
u-law计算时先用0x84 - sample(小于0)或者sample + 0x84,然后对应每一段使用不同的移位值得到最终的8bit结果
已知G711是将S16压缩为S8,于是输入必是S16
假设输入PCM数据为0b0000 0100 1101 0010,即0x1234
- 1、取得范围值,查表得
+2014 to +991 in 16 intervals of 64 - 2、得到基础值为
0xA0 - 3、得到间隔数
interval number = 64 - 4、得到区间基本值
2014 - 5、当前值
0x1234和区间基本值差异2014 - 1234 = 780 - 6、
偏移值 = 780 / 间隔数 = 780 / 64,取整为12 - 7、输出为
0xA0 + 12 = 0xAC
代码
#define BIAS (0x84) /* Bias for linear code. 线性码偏移值*/
#define CLIP 8159 //最大量化级数量
static int seg_uend[8] = {0x3F, 0x7F, 0xFF, 0x1FF,
0x3FF, 0x7FF, 0xFFF, 0x1FFF};
static int search(
int val, /* changed from "short" *drago* */
int *table,
int size) /* changed from "short" *drago* */
{
int i; /* changed from "short" *drago* */
for (i = 0; i < size; i++) {
if (val <= *table++)
return (i);
}
return (size);
}
int linear2ulaw( int pcm_val) /* 2's complement (16-bit range) */
{
int mask;
int seg;
int uval;
/* Get the sign and the magnitude of the value. */
pcm_val = pcm_val >> 2;
if (pcm_val < 0) {
pcm_val = -pcm_val;
mask = 0x7F;
} else {
mask = 0xFF;
}
if ( pcm_val > CLIP ) pcm_val = CLIP; /* clip the magnitude 削波*/
pcm_val += (BIAS >> 2);
/* Convert the scaled magnitude to segment number. */
seg = search(pcm_val, seg_uend, 8);
/*
* Combine the sign, segment, quantization bits;
* and complement the code word.
*/
if (seg >= 8) /* out of range, return maximum value. */
return (0x7F ^ mask);
else {
uval = (seg << 4) | ((pcm_val >> (seg + 1)) & 0xF);
return (uval ^ mask);
}
}
int ulaw2linear( int u_val)
{
int t;
/* Complement to obtain normal u-law value. */
u_val = ~u_val;
/*
* Extract and bias the quantization bits. Then
* shift up by the segment number and subtract out the bias.
*/
t = ((u_val & QUANT_MASK) << 3) + BIAS;
t <<= (u_val & SEG_MASK) >> SEG_SHIFT;
return ((u_val & SIGN_BIT) ? (BIAS - t) : (t - BIAS));
}
G711A与G711U对比
和A-law画在同一个坐标轴中就能发现A-law在低强度信号下,精度要稍微高一些
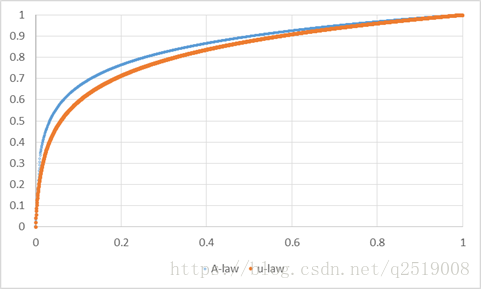
以上是两种算法的连续条件下的计算公式,实际应用中,我们确实可以用浮点数计算的方式把F(x)结果计算出来,然后进行量化,但是这样一来计算量会比较大,实际上对于A-law(A=87.6时),是采用13折线近似的方式来计算的,而μ-law(μ=255时)则是15段折线近似的方式。