RSA算法
- RSA算法流程
- 1.产生密钥
- 2.分组
- 加密
- 解密
- 实例
- RSA算法的计算问题
- 加密和解密中的计算
- 密钥产生过程的计算问题
- 改进的RSA算法
- RSA的安全性
- RSA的攻击
- 1.共模攻击
- 2.低指数攻击
RSA算法流程
RSA算法是迄今为止理论上最为成熟的公钥密码体制,并且已经得到广泛的应用。
1.产生密钥
产生密钥的过程如下:
- 选择两个保密的大素数P和q
- 计算n=p×q,φ(n)=(p-1)(q-1)
- 选择公钥e,e∈(1,φ(n))范围内的一个整数,且gcd(φ(n),e)=1
- 计算密钥d,d·e≡1 mod φ(n),即d≡e-1 mod φ(n)
- 以{e,n}为公钥,{d,n}为私钥
2.分组
将明文比特串分组,使得每个分组对应的十进制数小于n,即分组长度小于log2n
加密
对每个明文分组m,作加密运算:
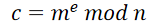
解密
对密文分组的解密运算如下:
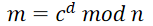
实例
这里以未分组的问题进行示例:
对于分组问题,当加密的时候,需要补零则在后面进行补零操作;解密时需要补0,则在每个分组前面进行补零操作
RSA算法的计算问题
加密和解密中的计算
RSA算法的加密和解密过程都为求一个整数的整数次幂再取模的运算。因此可能有如下问题:
1.中间结果非常大,超出计算机的整数取值范围。
2.指数的运算很复杂
针对不同的问题有不同的解决方法:
1.针对问题1,可以合理运用模运算的性质:
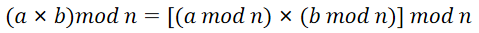
2.针对问题2,可以通过如下变形提高指数运算的有效性,减少运算次数。

基于该思想有快速指数算法如下:

应用解决方法的具体示例:
问题:求7560 mod 561.
解:将560协程二进制形式为1000110000,应用快速指数算法的结果为:

密钥产生过程的计算问题
密钥产生过程中的计算问题主要是大素数的确定问题:
产生密钥时,需要考虑两个大素数p、q的选取,以及e的选取和d的计算。因为n=pq在体制中是公开的,因此为了防止敌手通过穷搜索发现p、q的值,这两个素数应该是在一个足够大的整数集合中选取的大数。且RSA算法的优越性和有效地寻找大素数有密切联系。
寻找大素数一般先随机选取一个大的奇数(如用伪随机数产生器),然后用素性检验算法检验选择的奇数是否是素数,若不是,则选取另一大奇数,直到满足条件为止。后续工作可由Euclid算法完成
改进的RSA算法
改进的RSA算法是利用中国剩余定理来提高解密运算的速度。其解密过程如下:
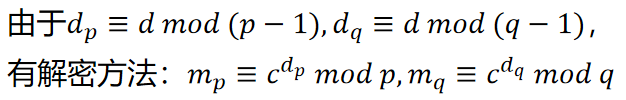
由中国剩余定理,有解:
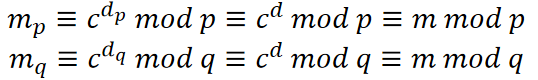
且已经表明,改进后的算法可以很大程度上减少解密运算时间
RSA的安全性
RSA的安全性是基于分解大整数的困难性假定。
且能够证明由n直接确定n的欧拉函数等价于对n的分解。
因此RSA的安全性对密钥的选取提出了大小的注意,除此还对p和q提出了以下要求:
1.|p-q|要大
2.p、q的选取要保证能使t很大,才能抵抗重复加密攻击
RSA的攻击
RSA由于参数选择不当会存在一下两种攻击
1.共模攻击
共模攻击就是指由于模数相同从而容易造成的攻击方法。可通过给用户设置不同的模数来进行抵抗
2.低指数攻击
低指数攻击是指用户的加密指数很小,攻击者利用中国剩余定理从而求解出m的攻击方法