GANs
生成对抗网络(Generative Adversarial Networks, GANs) 是一种用于捕获训练数据的**分布(distribution)**的神经网络。通过学习到的分布,可以创造新的数据。GAN由两个部分组成:
生成器(generator):用 G ( z ) G(z) G(z)表示,输入是(一般为正态分布采样的)随机噪声 z z z,输出是和训练数据等大的“fake”数据;判别器(discriminator):用 D ( x ) D(x) D(x)表示,用来判断输入数据 x x x是否为真正的训练数据,输出是一个 [ 0 , 1 ] [0,1] [0,1]区间的标量,输出值越大表示 D D D判定 x x x更可能是真实训练数据,越小则更可能是假的数据。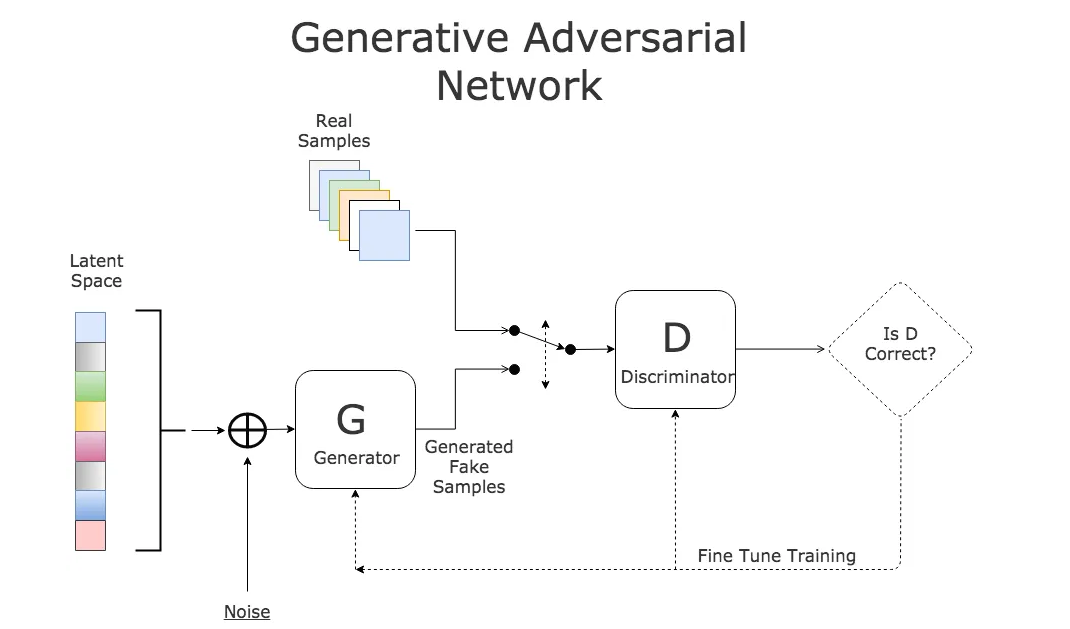
生成器和判别器之间是一个零和博弈的过程:生成器的效果越好,则判别器的正确率越低,反之亦然。在训练过程中,生成器的目的是“让判别器判断错误”,因此会生成越来越接近真实训练数据的假数据,这个过程也是学习训练数据分布的过程;判别器的目的则是“更好地区分真实数据和假数据”,因此学习过程会提高它的判别能力。
以上是一个感性的认知,在神经网络学习的框架下,需要定义一个具体的损失函数(loss),来对生成器和判别器的参数进行梯度更新。定义损失函数:
L G A N = E x [ l o g D ( x ) ] + E z [ l o g ( 1 − D ( G ( z ) ) ) ] , L_{GAN}=\mathbb{E}_{x}{[logD(x)]}+\mathbb{E}_{z}{[log(1-D(G(z)))]}, LGAN=Ex[logD(x)]+Ez[log(1−D(G(z)))],
式中的 x ∼ p d a t a ( x ) x \sim p_{data}(x) x∼pdata(x)取自训练数据, z ∼ p n o i s e ( z ) z\sim p_{noise}(z) z∼pnoise(z)为生成器 G G G的随机噪声(一般满足正态分布)输入, E \mathbb{E} E表示期望。
对于判别器 D D D,我们的目的是:真实数据 x x x, D ( x ) D(x) D(x)尽量更大;假数据 G ( z ) G(z) G(z), D ( x ) D(x) D(x)尽量更小,亦即 1 − D ( x ) 1-D(x) 1−D(x)尽量更大。因此判别器的训练过程的损失函数为 − L G A N -L_{GAN} −LGAN。
对于生成器 G G G,我们的目的是:真实数据 x x x,与 G G G无关,可以当做一个常数;假数据 G ( z ) G(z) G(z),希望判别器“认为它是真实数据”,也就是希望 1 − D ( x ) 1-D(x) 1−D(x)尽量更小。因此生成器的训练过程的损失函数为 L G A N L_{GAN} LGAN。
综上,GAN的训练本质上是一种极大极小博弈(minimax game):
min G max D L G A N \min_{G}\max_{D} L_{GAN} GminDmaxLGAN
理论上,训练最终会收敛于 p n o i s e = p d a t a p_{noise}=p_{data} pnoise=pdata,也就是生成器学习的概率分布与训练数据的一致,而判别器的输出等价于随机判定真假。但实际上GAN的训练过程很不稳定。
一个例子
使用CelebA人脸数据集训练一个DCGAN。所谓DCGAN,就是生成器和判别器都是卷积神经网络的GAN。训练后的生成器可以用随机噪声生成和训练集相似的人脸图像。
训练使用二进制交叉熵损失函数(BCELoss):
B C E L o s s ( x , y ) = − 1 n ∑ i [ y i l o g x i + ( 1 − y i ) l o g ( 1 − x i ) ] , BCELoss(x,y)=-\frac{1}{n}\sum_{i}{[y_ilogx_i+(1-y_i)log(1-x_i)]}, BCELoss(x,y)=−n1i∑[yilogxi+(1−yi)log(1−xi)],
这和之前讲到的 L G A N L_{GAN} LGAN非常相似,通过合理地选择标签 y y y就可以等价的表示 L G A N L_{GAN} LGAN。训练过程的一个iter的过程如下(关键步骤):
训练后的模型的生成器的输出和原始图片数据的对比:

代码在这里。