第十四届蓝桥杯大赛软件赛省赛（Python大学A组）

2023年蓝桥杯  省赛真题
Python大学A组

        试题A：特殊日期
        试题B：分糖果
        试题C：三国游戏
        试题D：平均
        试题E：翻转
        试题F：子矩阵
        试题G：阶乘的和
        试题H：奇怪的数
        试题I：子树的大小
        试题J：反异或01串

---

试题A：特殊日期   （5分）

【问题描述】

        记一个日期为 yy 年 mm 月 dd 日，统计从 2000 年 1 月 1 日到 2000000 年 1 月 1 日：有多少个日期满足年份 yy 是月份 mm 的倍数，同时也是 dd 的倍数。

【答案提交】

        这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只输出这个整数，输出多余的内容将无法得分。

【解析与方法】

        最简单粗暴的方法就是直接从2000年1月1日遍历到2000000年1月1日，使用这种方法写建议使用C++来写，运行速度快一些，Python跑的满。Python虽然有比较好用的datetime包，但是Python的datetime对象可以表示的日期范围从公元1年1月1日到公元9999年12月31日。题目给的最大日期已经超了，一跑就报错。所以还是直接暴力跑方便点且不容易出错。

【Python程序代码】

mon = [0,31,28,31,30,31,30,31,31,30,31,30,31]def run(x):  #判断是否为闰年    if x%400==0 or (x%4==0 and x%100!=0):        return True    return Falseres = 0for year in range(2000,2000000):    if run(year):        mon[2]=29    else:        mon[2]=28    for mm in range(1,13):        for dd in range(1,mon[mm]+1):            if year%mm==0 and year%dd==0:                res += 1print(res+1)  #前面只迭代到了1999999年12月31日，最后2000000年1月1日也是一个答案

最终结果为：35813063

 拓展：datetime对象的使用方法

from datetime import datetime, timedelta# 定义开始和结束日期start_date = datetime(2023, 1, 1)end_date = datetime(2024, 1, 1)# 定义时间间隔delta = timedelta(days=1)# 迭代日期范围while start_date <= end_date:    year = start_date.year    mon = start_date.month    day = start_date.day    print("%04d-%02d-%02d"%(year,mon,day))    #print(start_date.strftime("%Y-%m-%d"))    start_date += delta

---

试题B：分糖果     （5分）

【问题描述】

        两种糖果分别有9个和16个，要全部分给7个小朋友，每个小朋友得到的糖果总数最少为2个最多为5个，问有多少种不同的分法，糖果必须全部分完。
        如果有其中一个小朋友在两种方案中分到的糖果不完全相同，这两种方案就算作不同的方案。

【答案提交】

        这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只输出这个整数，输出多余的内容将无法得分。

【解析与方法】

        已知两种糖果的数量分别为9个和16个，每个小朋友最少分2个糖果，最多分5个糖果，由此可以把每中分发情况（a，b糖果每种分几个）都枚举出来。如下表格：

a	0	1	2	0	1	2	3	0	1	2	3	4	0	1	2	3	4	5
b	2	1	0	3	2	1	0	4	3	2	1	0	5	4	3	2	1	0

        因此根据已知的情况，可以采用暴力搜索的方式了，外加上方案成立的一个必要条件，糖果全部分完就可以确认方案是否成立。

【Python程序代码】

import syssys.setrecursionlimit(1000000)  #设置递归深度可以不需要a = [0,1,2,0,1,2,3,0,1,2,3,4,0,1,2,3,4,5]b = [2,1,0,3,2,1,0,4,3,2,1,0,5,4,3,2,1,0]ans = 0def dfs(u,c1,c2):    global ans    if u==7:        if not c1 and not c2:  #判断是否全部分完            ans += 1    else:        for i in range(len(a)):            if c1>=a[i] and c2>=b[i]:                dfs(u+1,c1-a[i],c2-b[i])dfs(0,9,16)print(ans)

最终结果：5067671

---

试题C：三国游戏     （10分） 

【问题描述】

        小蓝正在玩一款游戏，游戏中魏（X）、蜀（Y）、吴（Z）三个国家各自拥有一定数量的士兵X、Y、Z（一开始可以认为都是0）。游戏有n个可能会发送的事件，每个事件之间相互独立且最多只发送一次，当第i个事件发送时会分别让X、Y、Z增加  .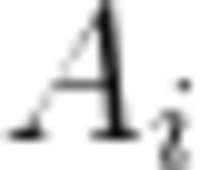

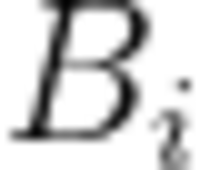
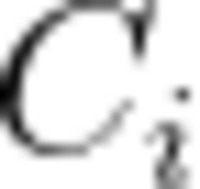        当游戏结束时（所以事件的发生与否已经确定），如果X,Y,Z的其中一个大于另外两个之和，我们认为其获胜。例如，当X>Y+Z时，我们认为魏国获胜，小蓝想知道游戏结束时，如果有其中一个国家获胜，最多发生了多少个事件？如果不存在任何一个让某个国家获胜的情况，请输出-1。

【输入格式】

        输入的第一行包含一个整数n。
        第二行包含n个整数表示A，相邻整数之间使用一个空格分隔
        第三行包含n个整数表示B，相整数之间使用一个空格分隔
        第四行包含n个整数表示C，相邻整数之间使用一个空格分隔

【输出格式】

        输出一行包括一个整数表示答案。

【样例输入】

31 2 22 3 21 0 7

【样例输出】

2

【测评用例与规模】

        对于 40% 的评测用例，n < 500;
        对于 70%的评测用例，n<5000;对于所有评测用例，，.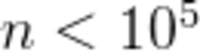

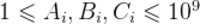【解析与方法】

        首先明确游戏结束时（所以发事情发生与否已经确定）仅仅只表示一次游戏会发生1，2...n这几件事情。可能在过程中会出现比如X>Y+Z的情况，此时并不表示某魏国获胜了。而是要等到全部事情发生后比对X与Y+Z的情况才能判断（省赛中误解了导致寄掉了）。理解后难度就直行下降了。因此可以枚举魏、蜀、吴三个国家想要获胜最多事情数量，然后取最大值即是答案。
        假设魏国获胜：令new_X =[ Ai - Bi - Ci].  1<=i<=n
        为使发生的事件最多，需要从new_Xi最大的地方开始发生，sum_X += new_Xi
        当sum_X<=0时，结束。

【Python程序代码】       

n = int(input())A = list(map(int,input().split()))B = list(map(int,input().split()))C = list(map(int,input().split()))new_X = sorted([ A[_] - B[_] - C[_] for _ in range(n) ],reverse=True)new_Y = sorted([ B[_] - A[_] - C[_] for _ in range(n) ],reverse=True)new_Z = sorted([ C[_] - A[_] - B[_] for _ in range(n) ],reverse=True)ans,resX,resY,resZ,sum_X,sum_Y,sum_Z = 0,0,0,0,0,0,0for i in range(n):    sum_X,sum_Y,sum_Z =  sum_X + new_X[i], sum_Y + new_Y[i], sum_Z + new_Z[i]    resX = resY = resZ = i + 1    if sum_X>0:ans = max(ans,resX)    if sum_Y>0:ans = max(ans,resY)    if sum_Z>0:ans = max(ans,resZ)    if sum_X<=0 and sum_Y<=0 and sum_Z<=0:breakprint(ans if ans else -1)

---

试题D：平均    （10分）

【问题描述】

        有一个长度为n的数组(n是10的倍数)，每个数a都是区间[0, 9]中的整数。小明发现数组里每种数出现的次数不太平均，而更改第i个数的代价为bi，他想更改若干个数的值使得这10种数出现的次数相等(都等于n/10)，请问代价和最少为多少。

【输入格式】

        输入的第一行包括一个正整数n。
        接下来n行，第i行包括两个整数ai，bi，用一个空格分隔。

【输出格式】

        输出包括一个正整数表示答案。

【样例输入】

101 11 21 32 42 52 63 73 83 94 10

【样例输出】

27

【样例说明】 

        只更改第 1,2,4,5,7,8个数，需要花费代价1+2+4+5+7+8=27

【测试用例与规模】

        对于20%的评测用例，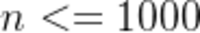
        对于所以的评测用例，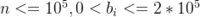

【解析与方法】

        应该是属于最简单编程题了，avg = n/10，遍历0~9，如果某个数的数量大于avg则需要改变num[i] - avg个数字，直接选取全部i数字改变需要代价最小的前num[i]-avg个数字即可。

 【Python程序代码】

n = int(input())num,avg,res = [[]for i in range(10)],n//10,0for i in range(n):  a,b = map(int,input().split())  num[a].append(b)for i in range(10):  if len(num[i])>avg:    num[i].sort()    for _ in range(len(num[i])-avg):      res += num[i][_]print(res)

---

试题E：翻转     （15分）

【问题描述】

        小蓝用黑白棋的n个棋子排成了一行，他在脑海里想象出了一个长度为 n的01串T，他发现如果把黑棋当做1，白棋当做0，这一行棋子也是一个长度为n的01串S。
        小蓝决定，如果在S中发现一个棋子和它两边的棋子都不一样，就可以将其翻转变成另一个颜色。也就是说，如果S中存在子串 101或者010，就可以选择将其分别变为111和000，这样的操作可以无限重复。
        小蓝想知道最少翻转多少次可以把S变成和一模一样

【输入格式】

        输入包含多组数据
        输入的第一行包含一个正整数 D表示数据组数
        后面2D行每行包含一个01串，每两行为一组数据，第 2i-1行为第i组数据的Ti，第2i行为第i组数据的Si，Si和Ti度均为n。

【输出格式】

        对于每组数据，输出一行包含一个整数，表示答案，如果答案不存在请输出-1。

【样例输入】

2100011110101010100011000

【样例输出】

2-1

【测评用例与规模】

        对于20%的测评用例，.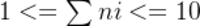

        对于所以的测评用例，保证.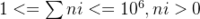

【解析与方法】

        由题目给出的S中若存在101、010.则可分别变成111、000，即任意连续三位若中间与左右两边不同则可以把中间的变成与左右两边相同。若将101或010变成111或000后，我们可以发现其不会对其他位置有影响，也就是不会发生连锁反应，也就是在比对Si和Ti时，若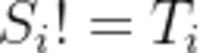，则判断Si是否符合翻转的条件，如果不符合翻转的条件则S不能变成T。

【Python程序代码】

tt = int(input())for i in range(tt):  t = list(input())#把s变成t  s = list(input())  cnt,flag = 0,1  for i in range(len(s)):    if s[i]!=t[i]:      if i-1>=0 and i+1<len(s) and s[i+1]!=s[i] and s[i-1]!=s[i]:        s[i],cnt = s[i+1],cnt+1      else:        flag = 0;break  print(cnt if flag else -1)

---

试题F：子矩阵     （15分）

【题目描述】

        给定一个nxm(n行m列)的矩阵。设一个矩阵的价值为其所有数中的最大值和最小值的乘积。求给定矩阵的所有大小为a xb (a 行列)的子矩阵的价值的和。
        答案可能很大，你只需要输出答案对998244353 取模后的结果。

【输入格式】

        输入的第一行包含四个整数分别表示n，m，a，b，相邻整数之间使用一个空格分隔。接下来
n行每行包含m个整数，相邻整数之间使用一个空格分隔，表示矩阵中的每个数Aij。

【输出格式】

        输出一行包含一个整数表示答案。

【样例输入】

2 3 1 21 2 34 5 6

【样例输出】

58

【样例说明】

        1x2+2x3+4x5+5x6=58.

【测评用例规模与约定】

        对于40%的测评用例，.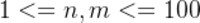
        对于70%的测评用例，.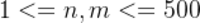
        对于所以的测评用例，.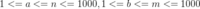

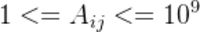
【解析与方法】

        暴力是显然不能通过全部测试数据的，需要得到每一个a*b大小的矩阵的最大值和最小值，可以先考虑得到每一行长度为b的窗口中的最大值和最小值，然后在这个基础上求出每一列长度为a的窗口的最大值和最小值。就可以预处理出来每个子矩阵中的最大值和最小值。要求一个滑动窗口中的最大值和最小值是一个基本的单调队列问题。

【Python程序与代码】

n, m, a, b = map(int, input().split())s,num_max,num_min,n_max,n_min,res = [[0] * (n + 2) for _ in range(n + 2)],[],[],[],[],0for i in range(1, n + 1):    s[i][1:m + 1] = map(int, input().split())def get_min(a, k, m):    tep,q,hh,tt = [],[0]*1010,0,-1    for i in range(1, m + 1):        if hh <= tt and q[hh] <= i - k: hh += 1  # 判断是否出了窗口        while hh <= tt and a[i] <= a[q[tt]]: tt -= 1        tt,q[tt] = tt + 1,i        if i - k >= 0: tep.append(a[q[hh]])    return tepdef get_max(a, k, m):    tep,q,hh,tt = [],[0]*1010,0,-1    for i in range(1, m + 1):        if hh <= tt and q[hh] <= i - k: hh += 1  # 判断是否出了窗口        while hh <= tt and a[i] >= a[q[tt]]: tt -= 1        tt,q[tt] = tt + 1,i        if i - k >= 0: tep.append(a[q[hh]])    return tepfor i in range(1, n + 1):    temp = [0] + get_max(s[i][:m + 1], b, m)    num_max.append(temp)    temp = [0] + get_min(s[i][:m + 1], b, m)    num_min.append(temp)for i in range(1, m - b + 2):    t1 = [0]    for _ in range(n):        t1.append(num_max[_][i])    t1.append(0)    temp = get_max(t1, a, n)    n_max.append(temp)    t2 = [0]    for _ in range(n):        t2.append(num_min[_][i])    t2.append(0)    temp = get_min(t2, a, n)    n_min.append(temp)for i in range(len(n_max)):    for j in range(len(n_max[0])):        res += n_max[i][j] * n_min[i][j]print(res)

---

试题G：阶乘的和     （20分）

【问题描述】

        给定n个数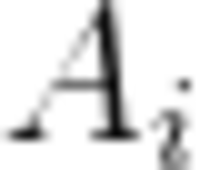，问能满足m!为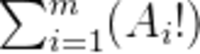的因数的最大的m是多少，其中m!表示m的阶乘，即1x2x3x···xm。

【输入格式】

        输入的第一行包含一个整数n。
        第二行包含n个整数，分别表示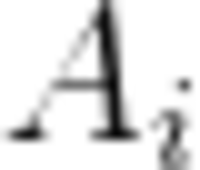，相邻整数之间使用一个空格分隔。

【输出格式】

        给出一行包括一个整数表示答案。

【样例输入】

32 2 2

【样例输出】

3

【测评用例规模与约定】

        对于40%的测评用例，.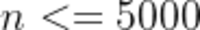
        对于所以的测评用例，.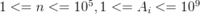

【解析与方法】

        首先明确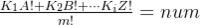，这个式子中num为整数时成立的条件，通过对分子提取公因数得到公因数为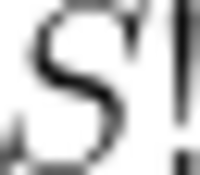，则m最大的值即为S。所以求解该问题只需要模拟阶乘的转换就可以。

【Python程序代码】

n = int(input())a = list(map(int,input().split()))a.sort()st,i,cnt = a[0],0,0while i<n:  while i<n and a[i]==st:    cnt += 1    i += 1  if cnt and cnt%(st+1)==0:    cnt,st = cnt//(st+1),st+1    if i==n:      while cnt and cnt%(st+1)==0:        cnt,st = cnt//(st+1),st+1  else:    breakprint(st)

---

试题H：奇怪的数     （20分）

【问题描述】

        小蓝最近在找一些奇怪的数，其奇数数位上是奇数，而偶数数位上是偶数同时，这些数的任意5个连续数位的和都不大于m。
        例如当m=9时，10101和12303 就是奇怪的数，而12345 和11111则不是。
小蓝想知道一共有多少个长度为n的上述的奇怪的数。你只需要输出答案对998244353取模的结果。

【输入格式】

        输入一行包含两个整数 n,m，用一个空格分隔。

【输出格式】

        输出一行包含一个整数表示答案。

【样例输入】

5 5

【样例输出】

6

 【测评用例规模与约定】

        对于30%的测评用例，n<=12;
        对于60%的测评用例，n<=5000;
        对于所以的测评用例，.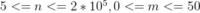

【解析与方法】

        需要连续验证5个数位上的数字之和是否大于m，设置状态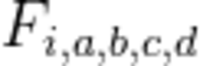，表示第i-3个数位上的数字是a，i-2：b，i-1：c，i：d的奇怪的数有多少个。所以有：

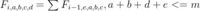
        时间复杂度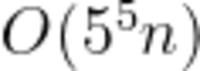，大概是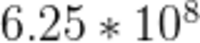次运算，大概率过不了。因此考虑维护F在第二维的前缀和。

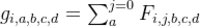
        转移方程：

        时间复杂度为，大概是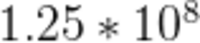次运算，对C++来说是可以直接过掉。都是Python可能会卡，在官网测试了一波，C++只需要40ms，Python只过70%。本题属实是本组别最难的题了。

【Python程序代码】

M,mod,ans,p,q = 12,998244353,0,1,0n, m= map(int, input().split())g = [[[[[0 for _ in range(M)] for _ in range(M)] for _ in range(M)] for _ in range(M)] for _ in range(2)]for a in range(p, 10, 2):      #维护二维的前缀和？ 预处理出前4位的情况    for b in range(q, 10, 2):        for c in range(p, 10, 2):            for d in range(q, 10, 2):                g[0][a + 2][b][c][d] = g[0][a][b][c][d] + int(a + b + c + d <= m)for i in range(5, n + 1):     #从第五位开始    p,q= p^1,q^1    for a in range(p, 10, 2):        for b in range(q, 10, 2):            for c in range(p, 10, 2):                for d in range(q, 10, 2):                    f = m - a - b - c - d  #计算f值                    if q != (f & 1):f -= 1   #余数f与当前位置的奇偶性不同则f--   q表示奇偶情况                    if f > 8 + p:f = 8 + q   #控制余数f在0~9范围内                    g[i % 2][a + 2][b][c][d] = (g[i % 2][a][b][c][d] + (0 if f < q else g[(i + 1) % 2][f + 2][a][b][c])) % modfor b in range(q, 10, 2):    for c in range(p, 10, 2):        for d in range(q, 10, 2):            f = m - b - c - d            if f < p:continue            if p != (f & 1):f -= 1            if f > 8 + p:f = 8 + p            ans = (ans + g[n % 2][f + 2][b][c][d]) % modprint(ans)

【C语言程序代码】

#include <stdio.h>const int M = 12, mod = 998244353;int n, m, ans, g[2][M][M][M][M];int main() {    scanf("%d %d", &n, &m);    int p = 1, q = 0;    //维护二维的前缀和 预处理出前4位的情况     for (int a = p; a < 10; a += 2)        for (int b = q; b < 10; b += 2)            for (int c = p; c < 10; c += 2)                for (int d = q; d < 10; d += 2) {                    g[0][a + 2][b][c][d] = g[0][a][b][c][d] + (a + b + c + d <= m);                }    //从第五位开始     for (int i = 5; i <= n; ++i) {        p ^= 1, q ^= 1;  //移动一位奇数偶数的相对位置发送变化         for (int a = p; a < 10; a += 2)            for (int b = q; b < 10; b += 2)                for (int c = p; c < 10; c += 2)                    for (int d = q; d < 10; d += 2) {                        int f = m - a - b - c - d;   //计算f值                         if (q != (f & 1)) --f;   //余数f与当前位置的奇偶性不同则f--    q表示奇偶情况                         if (f > 8 + p) f = 8 + q;   // 控制余数f在0~9范围内//状态转移                         g[i & 1][a + 2][b][c][d] = (g[i & 1][a][b][c][d] + (f < q ? 0 : g[~i & 1][f + 2][a][b][c])) % mod;                    }    }    for (int b = q; b < 10; b += 2)        for (int c = p; c < 10; c += 2)            for (int d = q; d < 10; d += 2) {                int f = m - b - c - d;                if (f < p) continue;                if (p != (f & 1)) --f;                if (f > 8 + p) f = 8 + p;                ans = (ans + g[n & 1][f + 2][b][c][d]) % mod;            }    printf("%d", ans);}

---

试题I：子树的大小     （25分）

【问题描述】

        给定一棵包含n个结点的完全m又树，结点按从根到叶、从左到右的顺序依次编号。例如下图是一个拥有 11个结点的完全3又树。

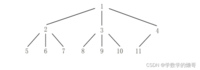
        你需要求出第k个结点的子树的结点数。 

【输入格式】

        输入包含多组询问。
        输入的第一行包含一个整数T，表示询问次数。
        接下来行，每行包含三个整数 n，m，k，表示一组询问。

【输出格式】

        输出T行，每行包含一个整数表示对应询问的答案。

【样例输入】

31 2 111 3 474 5 3

【样例输出】

1224

【用例规模与约定】

        对于40%的测评用例，.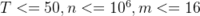
        对于所以的测评用例，.

【解析与方法】

        观察用例规模可知，想要建树是不可能的，所以需要从完全m叉树的特点入手。如下图：

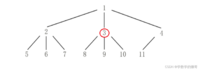
        先考虑当k为3的时候，即结点3的子树的结点个数的求法，设置一个左右指针l,r分别指向这一层子树的最左边和最右边的结点的编号。此时l=r=3。每次向下扩展一层并判断此时k结点最下层右侧的结点编号是否大于n，如果大于n则说明已经达到最大深度，同时再判断最左侧结点的编号是否小于等于n, 如果小于等于n，则最下层一共有n - ((l-1)*m+1)个结点，并退出循环。小于等于n的话继续向下扩展此时，r=(r*m+1) 、l=(l-1)*m+2。

【Python程序代码】

T = int(input())def solve(n,m,k):  l,r,res,mk = k,k,0,1  while True:    res += mk    if r*m+1>n:      if (l-1)*m+2<=n:        res += n- ((l-1)*m+1)      break    mk*=m    r = (r*m+1)    l = (l-1)*m+2  return resfor _ in range(T):  n,m,k = map(int,input().split())  print(solve(n,m,k))

---

试题J：反异或01串     （25分）

【问题描述】

        初始有一个空的01串，每步操作可以将0或1添加在左侧或右侧。也可以对整个串进行反异或操作: 取s' = rev(s)，其中s 是目前的01串，由表示逐位异或，rev(s)代表将 s翻转，也就是说取中心位置并交换所有对称的两个位置的字符。例如，rev(0101)=1010，rev(010) = 010，rev(0011)=1100。
        反异或操作最多使用一次 (可以不用，也可以用一次)。给定一个01串T，问最少需要添加多少个1才能从一个空01 串得到T，在本题中0可以添加任意个。

【输入格式】

输入一行包括一个01串表示给定的T。

【输出格式】

输出一行包括一个整数，表示最少需要添加多少个1.

【样例输入】

00111011

【样例输出】

3

【测评用例与规模】

        对于20%的测评用例，|T|<=10,对于40%的测评用例|T|<=500;
        对于40%的测评用例，|T|<=5000;对于80%的测评用例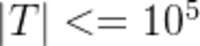
        对于所以的测评用例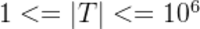，,保证T中仅包含0和1.

【解析与方法】

        首先读懂反异或操作，其实也就是一个长度为偶数的回文序列只需要一半数量的1通过反异或操作就可以创造出来，一个奇回文串的话要求中心字符不能为1，只能为0才能通过反异或操作以一半数量的1创造出来。所以题目可以转化为求一个满足上述条件的回文串，其使用1的数量最多。快速求回文串的长度的算法有马拉车算法（Manacher）通过马拉车算法可以预处理出来一个d[i]数组，表示以i为中心的回文串的半径，由此再用前缀和预处理优化求解可以把复杂度降到O(n)，不过常数比较大。用Python还是比较容易被卡。以下代码再C语言网中被卡了2个点。使用C++的话可以秒过。

【Python程序代码】

a = input()n, k = len(a), 1s = ['$', '#']for i in range(n):    k += 2    s.append(a[i])    s.append('#')n = k# 以上操作可以使新字符串为奇字符串# s[0]="$"是设置的哨兵# 设置数字1的前缀和函数pre = [0] * (n + 1)for i in range(1, n + 1):    if s[i] == '1':        pre[i] = pre[i - 1] + 1    else:        pre[i] = pre[i - 1]al = pre[n]d = [0] * (n + 1)co = 0# 回文半径d[i],即以i为中心半径为d[i],包括中心idef get_d():    global d    global co    d[1] = 1    l, r = 0, 1    for i in range(2, n + 1):        if i <= r:            d[i] = min(d[r - i + l], r - i + 1)        while i + d[i] <= n and i - d[i] >= 0 and s[i - d[i]] == s[i + d[i]]:            d[i] += 1        if i + d[i] - 1 > r:            l = i - d[i] + 1            r = i + d[i] - 1        if s[i] != '1':            co = max(co, pre[i - 1] - pre[i - d[i]])get_d()print(al - co)

【C++程序代码】

#include <iostream>#include <vector>#include <algorithm>using namespace std;int main() {    string a;    cin >> a;    int n = a.size(), k = 1;    vector<char> s(n * 2 + 3, '#');    s[0] = '$';    vector<int> pre(n * 2 + 3, 0);    for (int i = 0; i < n; ++i) {        k += 2;        s[k - 1] = a[i];    }    n = k;    for (int i = 1; i <= n; ++i) {        if (s[i] == '1') {            pre[i] = pre[i - 1] + 1;        } else {            pre[i] = pre[i - 1];        }    }    int al = pre[n];    vector<int> d(n + 1, 0);    int co = 0;    d[1] = 1;    int l = 0, r = 1;    for (int i = 2; i <= n; ++i) {        if (i <= r) {            d[i] = min(d[r - i + l], r - i + 1);        }        while (i + d[i] <= n && i - d[i] >= 0 && s[i - d[i]] == s[i + d[i]]) {            d[i] += 1;        }        if (i + d[i] - 1 > r) {            l = i - d[i] + 1;            r = i + d[i] - 1;        }        if (s[i] != '1') {            co = max(co, pre[i - 1] - pre[i - d[i]]);        }    }    cout << al - co << endl;    return 0;}