张士玉小黑屋
一个关注IT技术分享,关注互联网的网站,爱分享网络资源,分享学到的知识,分享生活的乐趣。
当前位置:首页 » 《随便一记》 - 第45页
Java多线程 - 创建线程池的方法 - ThreadPoolExecutor和Executors
发布 : zsy861 | 分类 : 《随便一记》 | 评论 : 0 | 浏览 : 346次
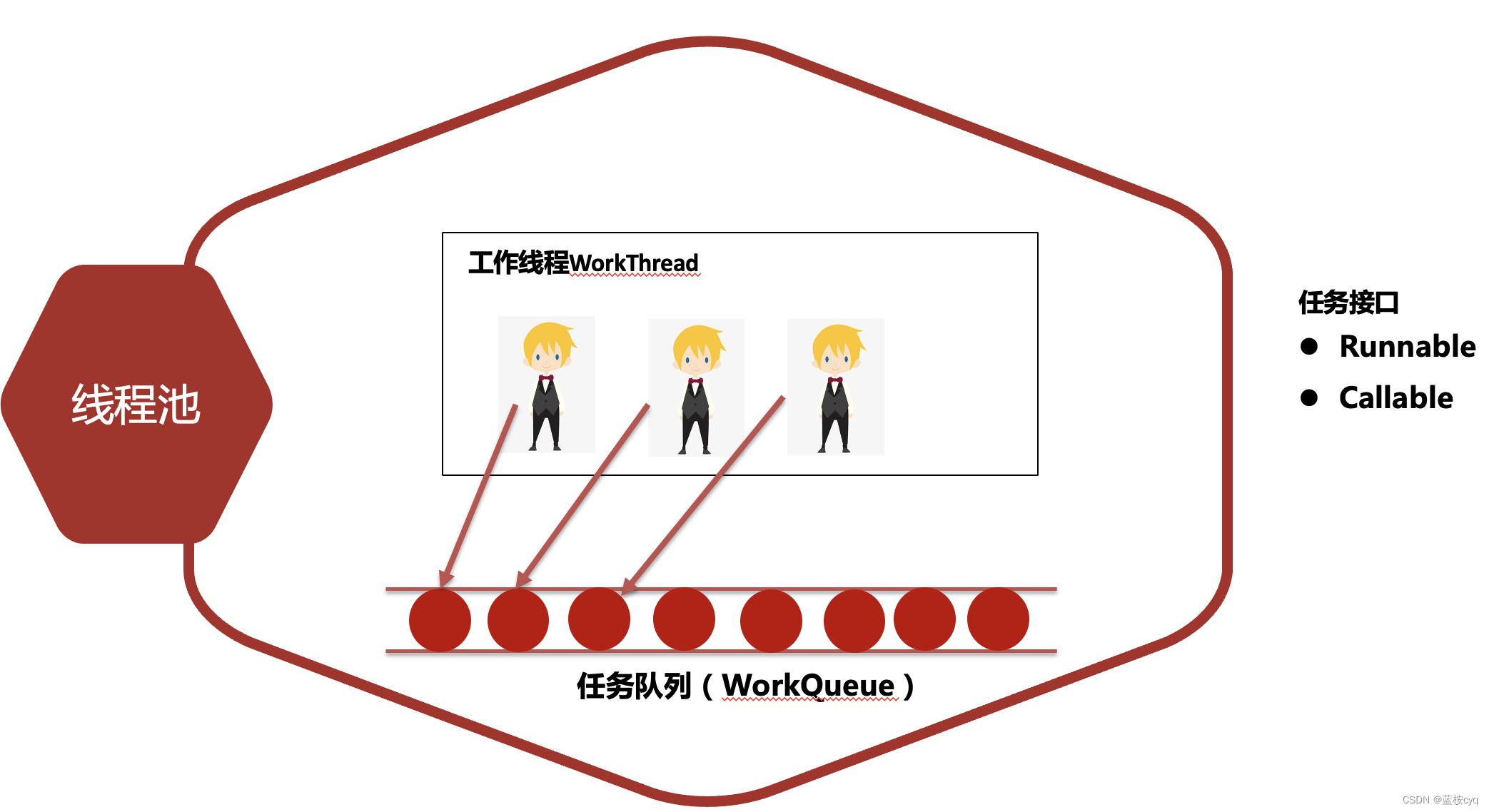
文章目录线程池(重点)线程池介绍实现线程池的方式方式一:实现类ThreadPoolExecutorThreadPoolExecutor构造器的参数线程池处理Runnable任务线程池处理Callable任务方式二:Executors工具类创建线程池线程池(重点)线程池介绍什么是线程池?线程池就是一个可以复用线程的技术。不使用线程池的问题:如果用户每发起一个请求,后台就创建一个新线程来处理,下次新任务来了又要创建新线程,而创建新线程的开销是很大的,这样会严重影响系统的性能。线程池工作原理:例如线程池中最多可以允许创建三个工作线程,也叫核心线程,前面三个任务来的时候会给前面三个任务单独创建三个线程;但是后面任务
Javaweb | 过滤器、配置、过滤器链、优先级
发布 : zsy861 | 分类 : 《随便一记》 | 评论 : 0 | 浏览 : 362次

?wei_shuo的个人主页?wei_shuo的学习社区?HelloWorld!过滤器概念过滤器(Filter)是处于客户端与服务器目标资源之间的一道过滤技术用户的请求和响应都需要经过过滤器过滤器作用执行地位在Servlet之前,客户端发送请求是,会先经过Filter,再到达目标Servlet中;响应时,会根据执行流程再次反向执行Filter可以解决多个Servlet共性代码的冗余问题过滤器可以对请求前和请求后进行逻辑处理编写过滤器ServletAPI中提供了一个Filter接口,开发人员编写一个Java类实现了这个接口即可,这个Java类称为过滤器实现过程编写Java类实现Filter接口在doFilter方法中编写拦截逻
强人工智能时代,区块链还有戏吗?
发布 : zsy861 | 分类 : 《随便一记》 | 评论 : 0 | 浏览 : 317次

最近很多人都在问我,ChatGPT把AI又带火了,区块链和Web3被抢了风头,以后还有戏吗?还有比较了解我的朋友问,当年你放弃AI而选择区块链,有没有后悔?这里有一个小背景。2017年初我离开IBM之后,跟CSDN的创始人蒋涛商量下一步的个人发展方向,选项有两个,一个是AI,一个是区块链。我本人在那个时候已经研究了两年的区块链了,所以当然想选这个。但是蒋涛坚定的认为AI的势头更猛、颠覆性更强,我经过仔细思考也同意了,所以从2017年初到年中,我短暂地做了半年的AI科技媒体,跑了不少会,采访了很多人,还浮光掠影的看了一些机器学习。不过到了8月,我就回归区块链方向,并且一路走到今天,所以对我个人说,确实存在一个所谓“放弃A而选择B”的历史选
Unity的协程详解
发布 : zsy861 | 分类 : 《随便一记》 | 评论 : 0 | 浏览 : 322次

一、协程的定义协程,即为协同程序.Unity中的协程由协程函数和协程调度器两部分构成.协程函数使用的是C#的迭代器,协程调度器则利用了MonoBehaviour中的生命周期函数来实现.协程函数实现了分步,协程调度器实现了分时. 注:因为协程分时分步执行的特性,当多个协程的耗时操作挤在同一时间执行也会造成卡顿。二、协程的用法usingSystem.Collection;usingUnityEngine;//定义一个协程函数,返回一个迭代器接口IEnumeratorCoroutineFunc(){Debug.Log("第一次进入");yieldreturnnull;Debug.Log("第二次进入");yieldreturnnu
Vue3【Axios网络请求(GET、POST 、并发请求、全局配置 )】(八)-全面详解(学习总结---从入门到深化)
发布 : zsy861 | 分类 : 《随便一记》 | 评论 : 0 | 浏览 : 398次
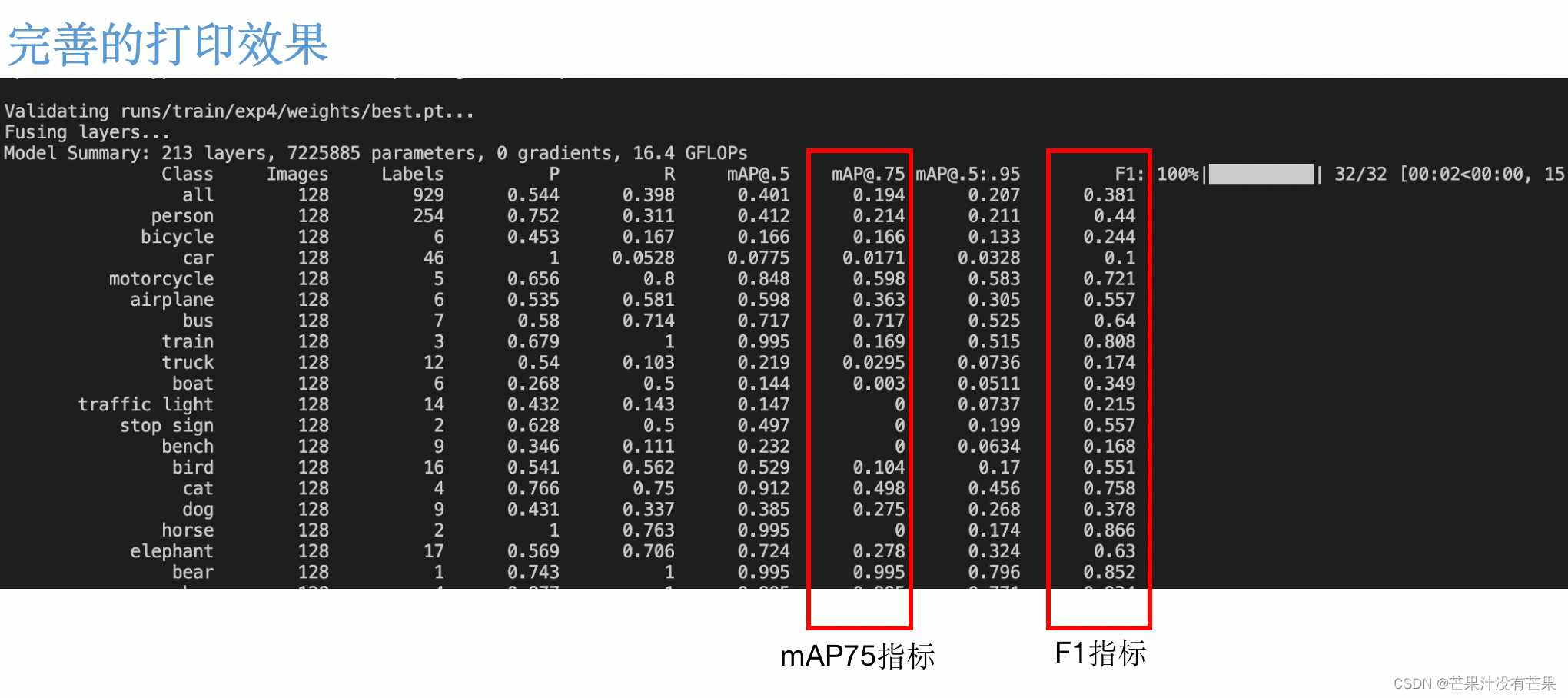
YOLOv5、YOLOv7改进之实验结果新增mAP75的值(一):新增打印mAP75的值,便于YOLOv5系列模型对比实验获取更多精度数据,丰富实验数据
发布 : zsy861 | 分类 : 《随便一记》 | 评论 : 0 | 浏览 : 649次
快排3种递归方法实现及优化(动图详解)
发布 : zsy861 | 分类 : 《随便一记》 | 评论 : 0 | 浏览 : 355次
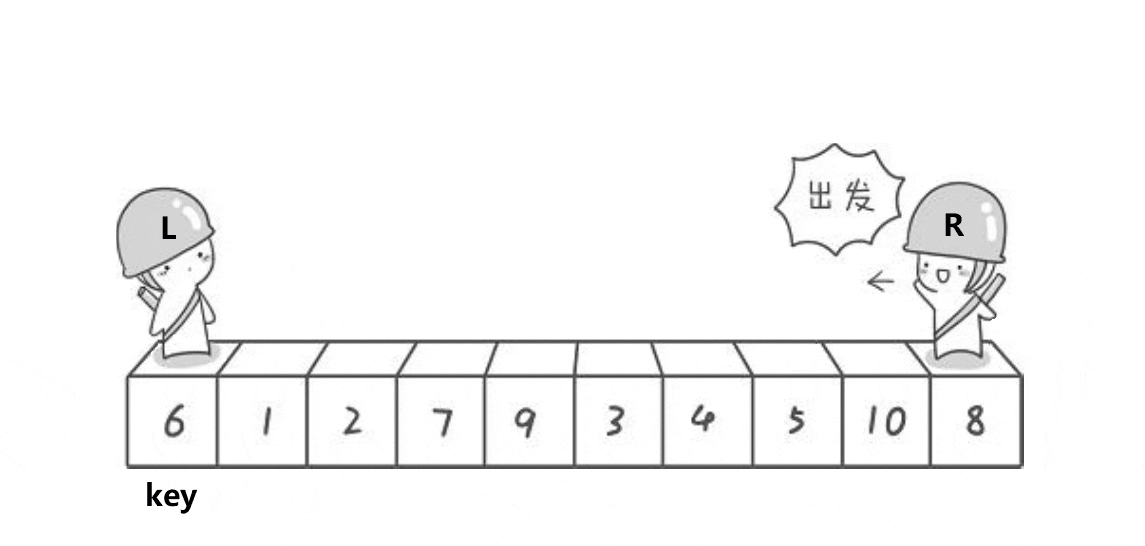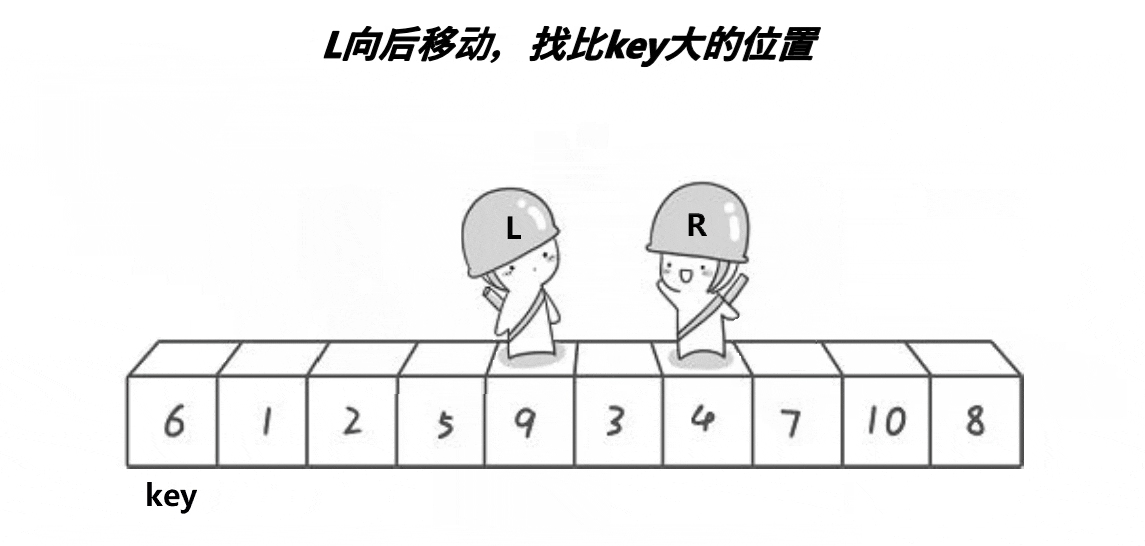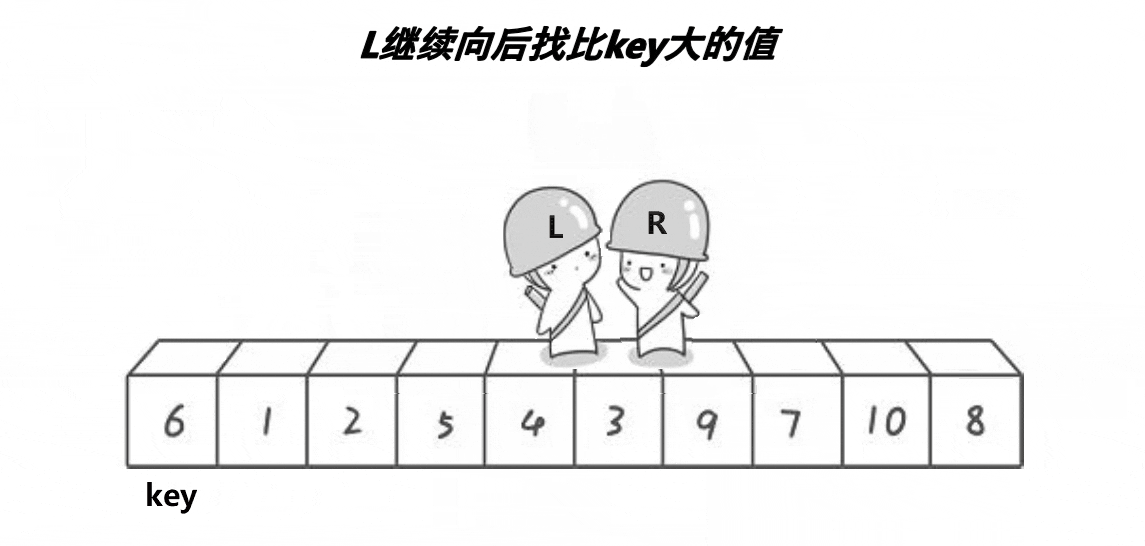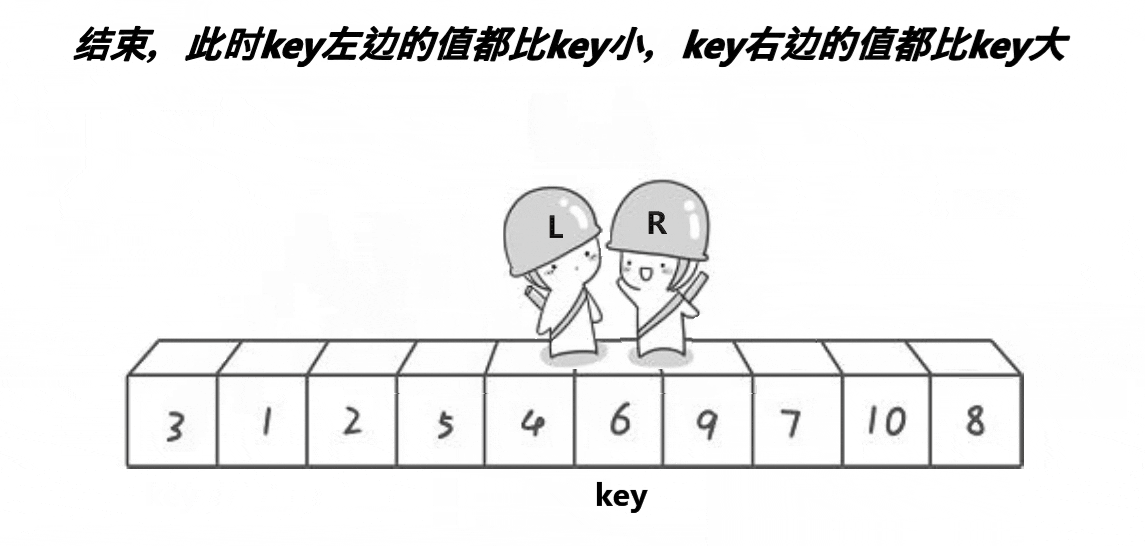
快速排序介绍: 快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法。其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。 这里我以升序为例。 简单来说:一趟排序的本质实际上是将一个或几个数据放到它应该在的位置上。例如:冒泡排序:每一趟都能将最大的数放到最后的位置。插入排序:每次插入的数与前面比较,满足条件就插入,不满足就移动。选择排序:每次选出最大/最小放到最前面或最后面。堆排序:堆顶可以得到最值,与最后的元素交换后,使得这个最值排在正确位置。向下调整是
ChatGPT的了解与初体验
发布 : zsy861 | 分类 : 《随便一记》 | 评论 : 0 | 浏览 : 374次

ChatGPT的了解与初体验什么是ChatGPT初体验1、场景一数据库sql编写2、场景二时间处理个人感觉下一个时代就是AI的时代,拥抱AI吧。什么是ChatGPT我们请它自己介绍一下自己吧!总体来说,就是能够用自然语言进行对话的智能机器人。初体验今日兴致来潮,便从两个简单业务小测一下咱们的ChatGPT。1、场景一数据库sql编写假设业务中需要分组统计数量,并同时统计总计数。提问它一下:这里可以看到咱们对话出现错别字,它也是可以正常处理的。WITHROLLUP函数,在之前本人并不熟悉,解决问题的同时又学到了新的知识点。WITHROLLUP总计列的分组字段值为NULL,看他如何处理。WITHROLLUP总计列的分组字段值为NULL,这
matlab遗传算法求解TSP旅行商问题
发布 : zsy861 | 分类 : 《随便一记》 | 评论 : 0 | 浏览 : 434次
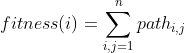
一、引言本文将用matlab编写遗传算法求解TSP旅行商问题,其实是对viafcccy原文章以及《MATLAB智能算法》中基于遗传算法TSP问题复现。但是原文中有一些细节,对像我这样的小白还是有些难度,因此在这里进行重新整理,这里也给出原文链接。1.1问题描述旅行商问题(travelingsalemanproblem,TSP)又被称为推销员问题、货郎担问题,该问题是最基本的路线问题。该问题寻求单一旅行者由起点出发,通过所有给定的需求点之后,最后再回到起点的最小路径成本,路径的限制是每个需求点只能拜访一次。最早的旅行商问题的数学模型是由Dantzig(1959)等学者提出的。旅行商问题是车辆路径问题(VRP)的特例,已证明旅行商问题是NP难问题。1.2算法实现1.2.1个体编码
Copyright © 2020-2022 ZhangShiYu.com Rights Reserved.豫ICP备2022013469号-1