深度学习和pytorch小结

视频学习机器学习概述机器学习的过程模型分类 深度学习概述神经网络结构的发展深度学习存在的局限性 深度学习基础万有逼近定理BP神经网络BP算法基本思想 多层神经网络的问题：梯度消失多层神经网络梯度消失解决方法 代码学习pytorch 基础练习螺旋数据分类生成相关的数据构建线性模型构建两层神经网络分类不同模型下的结果对比图不同优化函数的结果变化不同激活函数的结果变化 遇到的问题任务总结

视频学习

机器学习概述

机器学习 (Machine Learning) 是对研究问题进行模型假设，利用计算机从训练数据中学习得到模型参数，并最终对数据进行预测和分析的一门学科。

机器学习的过程

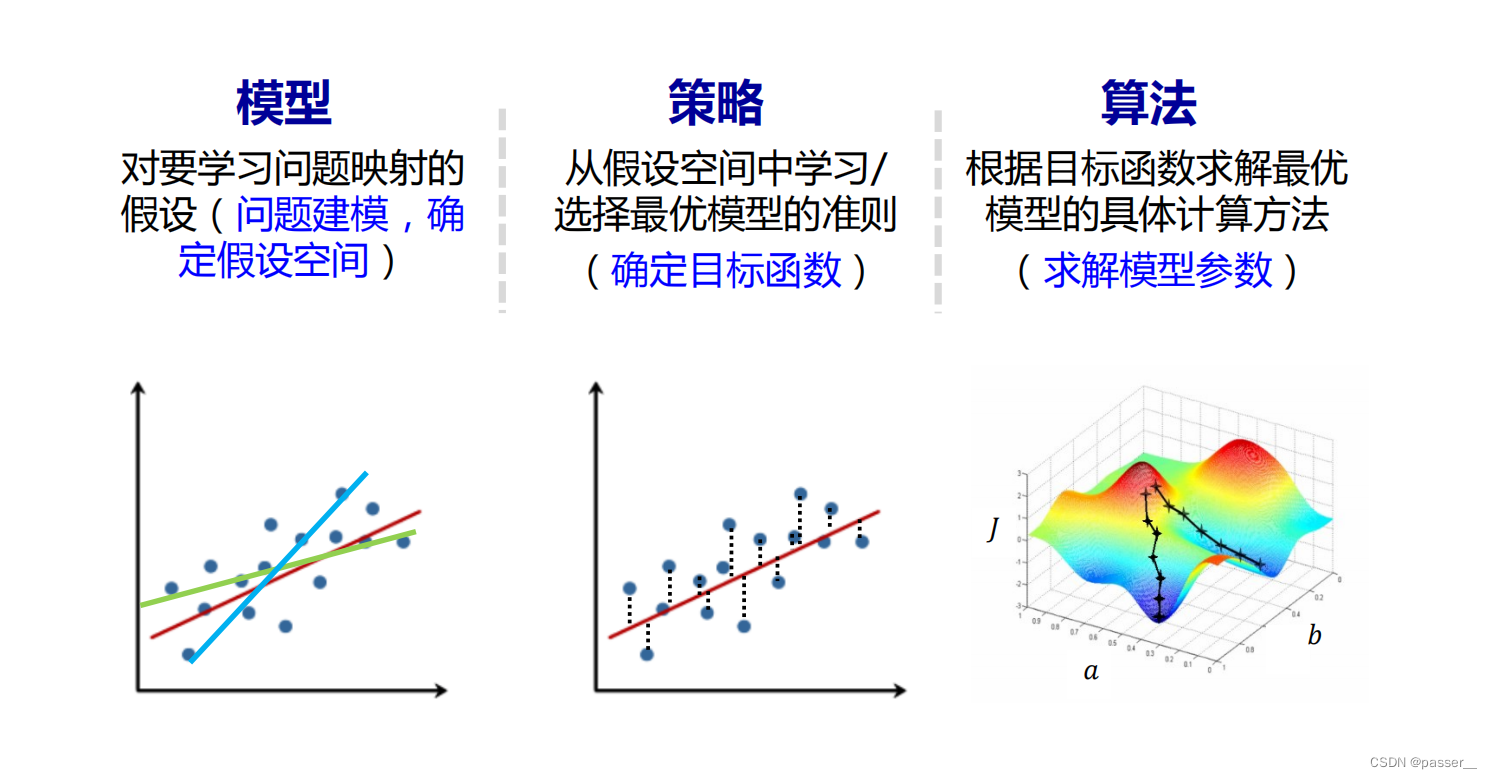
模型分类

无监督学习：样本没有标记。无监督学习从数据中学习模式，适用于描述数据，目的在于发现数据中模式/有意义信息
监督学习：样本具有标记(输出目标)。监督学习从数据中学习标记分界面 (输入-输出的映射函数)，适用于预测数据标记
半监督学习：部分数据标记已知，是监督学习和无监督学习的混合
强化学习：数据标记未知，但 知道与输出目标相关的反馈，适用决策类问题

参数模型：对数据分布进行假设，待求解的数据模式/映射可以用一组有限且固定数目的参数进行刻画。比如 线性回归、逻辑回归、感知机、K均值聚类
非参数模型：不对数据分布进行假设，数据的所有统计特性都来源于数据本身。比如K近邻、SVM、决策树、随机森林

生成模型： 对输入?和输出?的联合分布?(?, ?)建模，利用贝叶斯公式求解
判别模型： 对已知输入?条件下输出Y的条件分布?(?|?) 建模，直接预测出最可能的解

深度学习概述

深度学习是学习样本数据的内在规律和表示层次，这些学习过程中获得的信息对诸如文字，图像和声音等数据的解释有很大的帮助。它的最终目标是让机器能够像人一样具有分析学习能力，能够识别文字、图像和声音等数据。

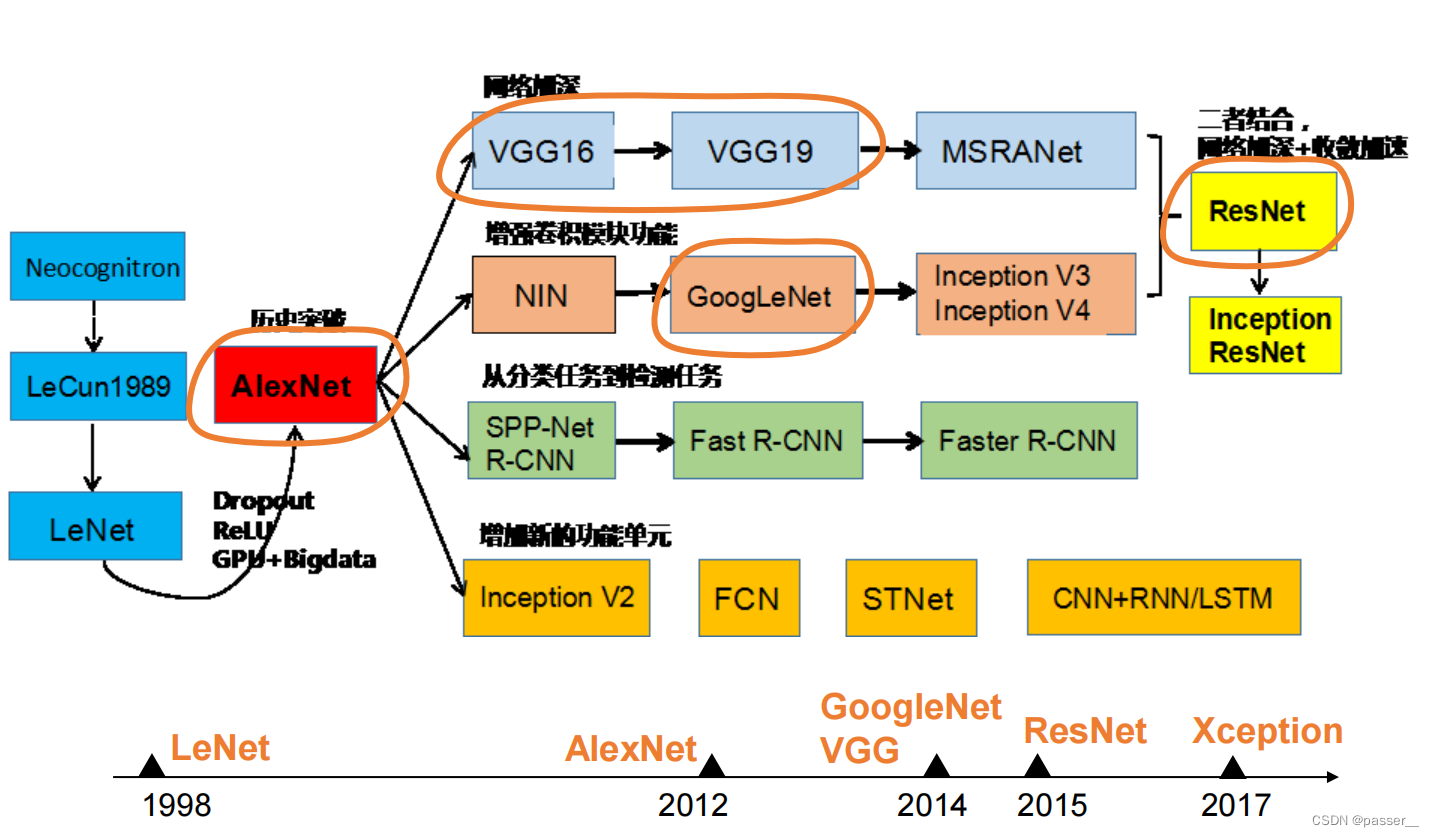
神经网络结构的发展

深度学习存在的局限性

算法输出不稳定，容易被“攻击”模型复杂度高，难以纠错和调试模型层级复合程度高，参数不透明端到端训练方式对数据依赖性强，模型增量性差专注直观感知类问题，对开放性推理问题无能为力人类知识无法有效引入进行监督，机器偏见难以避免

深度学习基础

万有逼近定理

如果一个隐层包含足够多的神经元，三层前馈神经网络（输入-隐层
-输出）能以任意精度逼近任意预定的连续函数。

BP神经网络

BP神经网络是这样一种神经网络模型，它是由一个输入层、一个输出层和一个或多个隐层构成，它的激活函数采用sigmoid函数，采用BP算法训练的多层前馈神经网络。

BP算法基本思想

BP算法全称叫作误差反向传播(error Back Propagation，或者也叫作误差逆传播)算法。其算法基本思想为：在2.1所述的前馈网络中，输入信号经输入层输入，通过隐层计算由输出层输出，输出值与标记值比较，若有误差，将误差反向由输出层向输入层传播，在这个过程中，利用梯度下降算法对神经元权值进行调整。

多层神经网络的问题：梯度消失

目前优化神经网络的方法都是基于BP，即根据损失函数计算的误差通过梯度反向传播的方式，指导深度网络权值的更新优化。其中将误差从末层往前传递的过程需要链式法则（Chain Rule）的帮助，因此反向传播算法可以说是梯度下降在链式法则中的应用。而链式法则是一个连乘的形式，所以当层数越深的时候，梯度将以指数形式传播。梯度消失问题和梯度爆炸问题一般随着网络层数的增加会变得越来越明显。在根据损失函数计算的误差通过梯度反向传播的方式对深度网络权值进行更新时，得到的梯度值接近0或特别大，也就是梯度消失或爆炸。

多层神经网络梯度消失解决方法

代码学习

pytorch 基础练习

**#一些函数的基本参数**ones(*size, *, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) → Tensor返回创建size大小的维度，里面元素全部填充为1full(size, fill_value, *, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) → Tensor返回创建size大小的维度，里面元素全部填充为fill_valuetorch.zeros(*size, *, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) → Tensor返回创建size大小的维度，里面元素全部填充为0randn_like(input, *, dtype=None, layout=None, device=None, requires_grad=False, memory_format=torch.preserve_format) -> Tensor返回一个和输入大小相同的张量，其由均值为0、方差为1的标准正态分布填充dtype            所需的数据返回张量的类型。默认值：如果为 None ，则默认为 input 的dtype layout           返回的张量的所需布局。默认值：如果为 None ，则默认为 input 的布局device           返回张量的所需设备。默认值：如果为 None ，则默认为 input 的设备requires_grad    如果需要在返回张量上保存梯度，默认为Falsetorch.linspace(start, end, steps=100, out=None) → Tensor返回一个1维张量，包含在区间start和end上均匀间隔的step个点。输出张量的长度由steps决定。

import torchx = torch.tensor(666)  #0维向量是一个标量print(x)#tensor(666)list = [1,2,3,4,5]x = torch.tensor(list) #一维张量(向量)print(x)#tensor([1, 2, 3, 4, 5])Ones  = torch.ones(2,3) #二维张量(矩阵)2*3 1矩阵Zeros = torch.zeros(2,3) # 2*3 0矩阵x = torch.empty(5,3)  # 构建5*3的未初始化的矩阵Random = torch.rand(5,3)  #构建5*3的随机初始化的矩阵print(Ones)print(Zeros)print(x)print(Random)tensor([[1., 1., 1.],        [1., 1., 1.]])tensor([[0., 0., 0.],        [0., 0., 0.]])tensor([[7.9534e-36, 0.0000e+00, 0.0000e+00],        [0.0000e+00, 0.0000e+00, 0.0000e+00],        [0.0000e+00, 0.0000e+00, 0.0000e+00],        [0.0000e+00, 0.0000e+00, 0.0000e+00],        [0.0000e+00, 0.0000e+00, 0.0000e+00]])tensor([[0.3447, 0.1758, 0.5167],        [0.3494, 0.1158, 0.9085],        [0.6784, 0.7626, 0.3200],        [0.8231, 0.3561, 0.2288],        [0.0197, 0.4146, 0.8990]])凡是用Tensor进行各种运算的，都是Function最终，还是需要用Tensor来进行计算的，计算无非是基本运算，加减乘除，求幂求余布尔运算，大于小于，最大最小线性运算，矩阵乘法，求模，求行列式基本运算包括： abs/sqrt/div/exp/fmod/pow ，及一些三角函数 cos/ sin/ asin/ atan2/ cosh，及 ceil/round/floor/trunc 等具体在使用的时候可以百度一下布尔运算包括： gt/lt/ge/le/eq/ne，topk, sort, max/min线性计算包括： trace, diag, mm/bmm，t，dot/cross，inverse，svd 等# 创建一个 2x4 的tensorimport torchlist = [[1,2,3,4],       [4,3,2,1]]x = torch.tensor(list)print(x.size(0),x.size(1),x.size(),sep='--')print(x.numel())     # 返回 x 中元素的数量#2--4--torch.Size([2, 4])#8list = [[1,2,3,4],       [4,3,2,1]]x = torch.tensor(list)print(x[0][1])    # 返回 第0行，第1列的数print(x[:,2])    # 返回 第2列的全部元素print(x[0,:])    # 返回 第0行的全部元素#tensor(2)#tensor([3, 2])#tensor([1, 2, 3, 4])# 创建一个 2x4 的tensorm = torch.tensor([[2, 5, 3, 7],                 [4, 2, 1, 9]])x = torch.arange(1,5)  m @ x                      #矩阵m和x叉乘m[[0], :] @ x              #m的第一行和x叉乘m + torch.rand(2, 4)       #m矩阵加上一个随机的2*4的矩阵print(m.t())               #m的转置矩阵#print(m.transpose(0, 1))  #m的转置矩阵 #tensor([49, 47])#tensor([49])#tensor([[2, 4],        [5, 2],        [3, 1],        [7, 9]])# 创建两个 1x4 的tensora = torch.Tensor([[1, 2, 3, 4]])b = torch.Tensor([[5, 6, 7, 8]])# 在 0 方向拼接 （即在 Y 方各上拼接）, 会得到 2x4 的矩阵print( torch.cat((a,b), 0))# 在 1 方向拼接 （即在 X 方各上拼接）, 会得到 1x8 的矩阵print( torch.cat((a,b), 1))#tensor([[1., 2., 3., 4.],        [5., 6., 7., 8.]])#tensor([[1., 2., 3., 4., 5., 6., 7., 8.]])

螺旋数据分类

生成相关的数据

#下载绘图函数!wget https://raw.githubusercontent.com/Atcold/pytorch-Deep-Learning/master/res/plot_lib.py#导入需要的包import randomimport torchfrom torch import nn, optimimport mathfrom IPython import displayfrom plot_lib import plot_data, plot_model, set_default# 因为colab是支持GPU的，torch 将在 GPU 上运行device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")print('device: ', device)# 初始化随机数种子。神经网络的参数都是随机初始化的，# 不同的初始化参数往往会导致不同的结果，当得到比较好的结果时我们通常希望这个结果是可以复现的，# 因此，在pytorch中，通过设置随机数种子也可以达到这个目的seed = 12345random.seed(seed)torch.manual_seed(seed)N = 1000  # 每类样本的数量D = 2  # 每个样本的特征维度C = 3  # 样本的类别H = 100  # 神经网络里隐层单元的数量X = torch.zeros(N * C, D).to(device)Y = torch.zeros(N * C, dtype=torch.long).to(device)for c in range(C):  #生成需要的数据    index = 0    t = torch.linspace(0, 1, N) # 在[0，1]间均匀的取10000个数，赋给t    # 下面的代码不用理解太多，总之是根据公式计算出三类样本（可以构成螺旋形）    # torch.randn(N) 是得到 N 个均值为0，方差为 1 的一组随机数，注意要和 rand 区分开    inner_var = torch.linspace( (2*math.pi/C)*c, (2*math.pi/C)*(2+c), N) + torch.randn(N) * 0.2        # 每个样本的(x,y)坐标都保存在 X 里    # Y 里存储的是样本的类别，分别为 [0, 1, 2]    for ix in range(N * c, N * (c + 1)):        X[ix] = t[index] * torch.FloatTensor((math.sin(inner_var[index]), math.cos(inner_var[index])))        Y[ix] = c        index += 1

构建线性模型

#构建一个只包含两个全连接层的线性模型learning_rate = 1e-3lambda_l2 = 1e-5# nn 包用来创建线性模型# 每一个线性模型都包含 weight 和 biasmodel = nn.Sequential(  #两个全连接层    nn.Linear(D, H),    nn.Linear(H, C))model.to(device) # 把模型放到GPU上# nn 包含多种不同的损失函数，这里使用的是交叉熵（cross entropy loss）损失函数criterion = torch.nn.CrossEntropyLoss()# 这里使用 optim 包进行随机梯度下降(stochastic gradient descent)优化optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, weight_decay=lambda_l2)# 开始训练for t in range(1000):    # 把数据输入模型，得到预测结果    y_pred = model(X)    # 计算损失和准确率    loss = criterion(y_pred, Y)    score, predicted = torch.max(y_pred, 1)    acc = (Y == predicted).sum().float() / len(Y)    print('[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f' % (t, loss.item(), acc))    display.clear_output(wait=True)    # 反向传播前把梯度置 0     optimizer.zero_grad()    # 反向传播优化     loss.backward()    # 更新全部参数    optimizer.step()

构建两层神经网络分类

# 这里可以看到，和上面模型不同的是，在两层之间加入了一个 ReLU 激活函数，使得神经网络拥有了非线性分类的能力model = nn.Sequential(    nn.Linear(D, H),    nn.ReLU(),    nn.Linear(H, C))

不同模型下的结果对比图

不同优化函数的结果变化

结果	参数变量
	两层全连接层和SGD优化
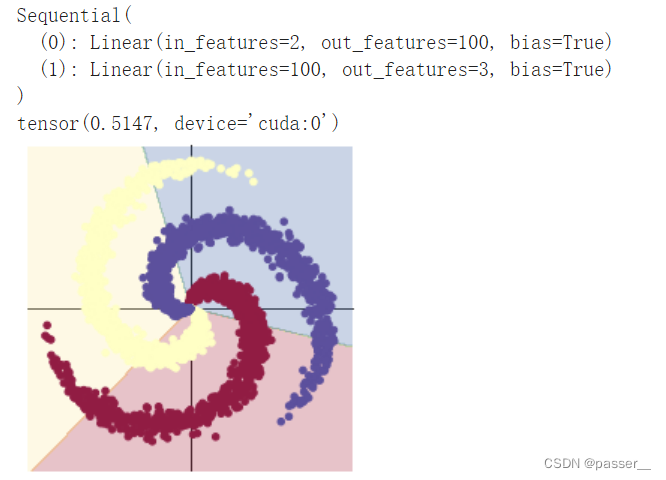	两层全连接层和Adam优化

不同激活函数的结果变化

结果	参数变量
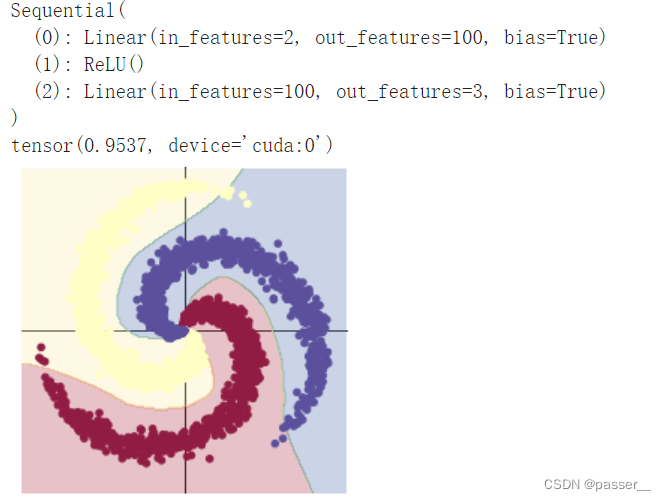	两层全连接层之间加入ReLu激活函数
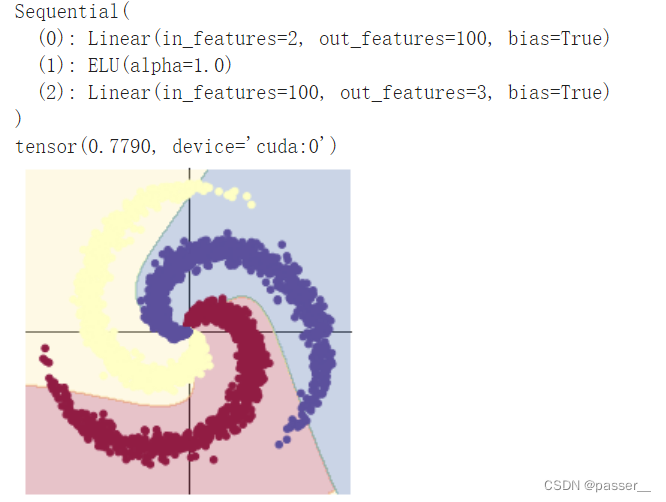	两层全连接层之间加入ELU激活函数
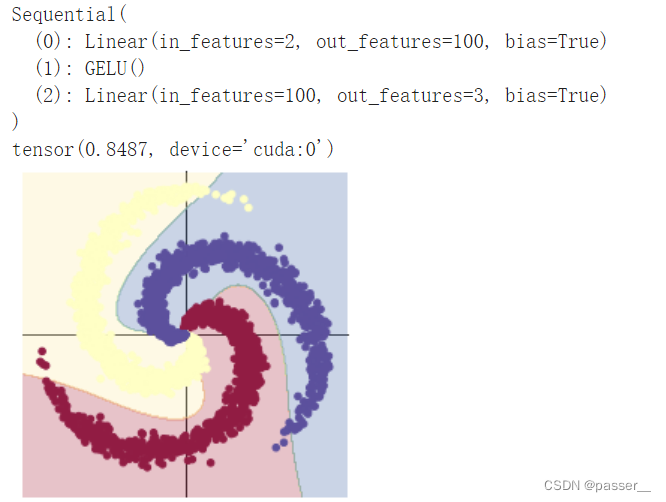	两层全连接层之间加入GELU激活函数
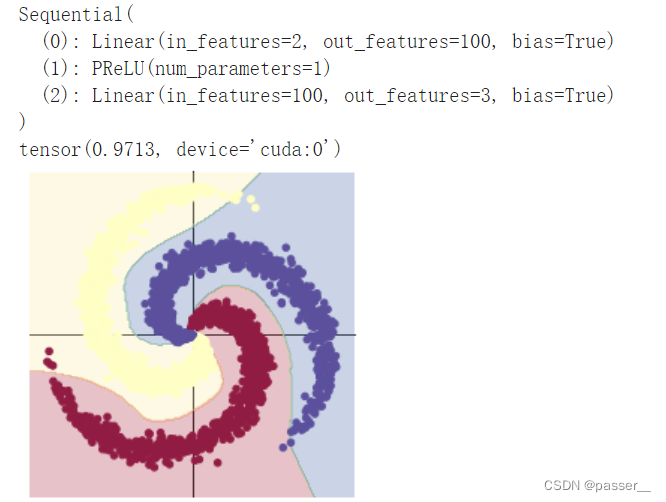	两层全连接层之间加入PRELU激活函数
	两层全连接层之间加入Hardshrink激活函数

遇到的问题

Tensor和tensor的区别
Tensor 是多维矩阵，矩阵的元素都是同一种数据类型。tensor 需要确切的数据对它进行赋值。叉乘过程过会报 类型不匹配的错误

任务总结

深度学习理论 60分钟入门深度学习工具-PyTorch