前言
这三个数据结构,相对于之前的来说比较常见,几乎都与线性表有关,很类似。最近期末复习本来打算不写了,但是为了使这个专栏比较完整,所以想一想还是写一下吧!其中大量重点因为没时间作图阐述,于是在网上找了写的好的引用过来的,偷了个大懒,请见谅!
温馨提示:字体蓝色点击可以直接进入原文
目录
- 前言
- 串
- 串的定义
- 串的实现
- 顺序串
- 链串
- 串的模式匹配
- BF算法
- KMP算法
- 数组
- 矩阵的压缩存储
- 对称矩阵
- 三角矩阵
- 三对角矩阵
- 稀疏矩阵
- 结语
串
串是重要的非数值处理对象,它是以字符作为数据元素的线性表。也是受限制的线性表.
串的定义
串( string)是由零个或多个字符组成的有限序列,又名叫字符串
下面是常用的串的概念:
串:零个或多个字符组成的有限序列。
串长度:串中所包含的字符个数。
空串:长度为0的串,记为:" “。
非空串:通常记为:S=” a1 a2 …… an " (n≥0) 其中:S是串名,双引号是定界符,双引号引起来的部分是串值 ,ai(1≤i≤n)是一个任意字符。
子串:串中任意个连续的字符组成的子序列。
主串:包含子串的串。
子串的位置:子串的第一个字符在主串中的序号。注意:空串是任意串的子串,任意串是其自身 的子串。
串的比较
串的比较是通过组成串的字符之间的比较来进行的。串的比较是按照对应字符的ASCII码进行的。
比较串相等时候先比较串的长度是否相等在比较串中对应字符是否相等。
下面是串的一些基本操作:
StrLength (s):求串s的长度。
StrAssign (s1, s2):赋值,将s2的值赋值给串s1。
Concat (s1, s2, s):连接,将串s2放在串s1的后面连接成一个新串s。
SubString (s, i, len):求子串,返回从串s的第i个字符开始取长为 len 的子 串。
StrCompare (s1, s2):串比较,若s1=s2,返回0;若s1<s2, 返回-1;若s1>s2, 返回1。
Index (s, t, pos):定位,返回子串t在主串s中首次出现的位置。若t不是s的子串,则返回0。
StrInsert (s, i, t):插入,将串t插入到串s中的第i个位置。
StrDelete (s, i,len):删除,在串s中删除从第i个字符开始的连续len个字符。
Replace (s, t,r):替换,在串s中用串r替换所有与串t相等的子串。
StrEmpty (s): 判断串空,如果串s为空则返回true。否则返回false。
StrCopy (t,s): 串拷贝,由串s复制得串t。
ClearString (s):清空串,若串s存在则将s清为空串。
DestroyString (s):销毁串,若串s存在则将s销毁掉。
串的逻辑结构和线性表极为相似,区别仅在于串的数据对象限定为字符集。在基本操作上,串和线性表有很大差别。线性表的基本操作主要以单个元素作为操作对象,如查找、插入或删除某个元素等;而串的基本操作通常以子串作为操作对象,如查找、插入或删除一个子串等。
串的实现
实现就从存储结构上面实现了,仍然从顺序存储与链式存储实现。
顺序串
顺序串类似于线性表的顺序存储结构,用一组地址连续的存储单元存储串值的字符序列。即数组,还有一个整型变量用来存储字符串长度。
#define MaxSize 50
typedef struct{
char ch[MaxSize];
int length;
}SString;
之前看到一篇顺序串操作总结很好的文章,大家可以看看 顺序串操作
链串
链串结构包括两部分,一个用来存放单个字符,还有一个用来存放下一个字符的地址。
typedef struct node{
char data;
struct node *next;
}LinkNode;
之前看到一篇链式串操作总结很好的文章,大家可以看看 链式串操作
串的模式匹配
串的模式匹配算法,是一种用来判断两个串之间是否具有主串与子串关系的算法。模式匹配算法有两种:普通模式匹配算法(BF算法)和快速模式匹配算法(KMP算法)。下面我们分别看一下它们是怎么回事。
BF算法
普通模式匹配算法,其实现过程没有任何技巧,就是简单粗暴地拿一个串同另一个串中的字符一一比对,得到最终结果。
看 详细BF算法明白BF算法
代码实现:
public int IndexOfBF(String S,String T,int pos){
char []a = S.toCharArray();
char []b = T.toCharArray();
int i=pos;int j=0;
while(i<S.length() && j<T.length()){
if(a[i]==b[j]){ // 继续比较
i++;j++;
}
else{ //i后退重新匹配
i=i-j+1;j=0;
}
}
if(j>=T.length()) //匹配成功
return i-T.length();
else //匹配失败
return 0;
KMP算法
快速模式匹配算法,比之前BF算法时间快很多,也比较难理解。
看 详细KMP算法明白KMP算法
代码实现:
public int IndexOfKMP(String S,String T,int pos){
char []a = S.toCharArray();
char []b = T.toCharArray();
int i=0;int j=0;
while(i<S.length() && j<T.length()){
if(j==-1 || a[i]==b[j]){ // 继续比较 必须j==-1在前面
i++;j++;
}
else{ //j后退重新匹配,i不变
j=next[j];
}
}
if(j>=T.length()) //匹配成功
return i-j;
else //匹配失败
return 0;
}
求next(j)代码实现
public void getNext(String T,int [] next){
char []b = T.toCharArray();
next[0]=-1;
int i=0,j=-1;
while(i < T.length()-1)
{
if(j==-1 || b[i]==b[j]){
++i;++j;
next[i]=j;
}
else
j=next[j];
}
}
数组
数组是由n (n>=1)个相同类型的数据元素构成的有限序列,每个数据元素称为一个数组元素,每个元素受n个线性关系的约束,每个元素在n个线性关系中的序号称为该元素的下标,并称该数组为n维数组,从某种意义上讲它是一种逻辑结构。
数组一旦被定义,其维度和维界不可变,数组除初始化和销毁外,只有存取元素和修改元素的操作。
数组从存储结构上讲有两种为:按行优先和按列优先。分别就是一行一行的存与一列一列的存。
二维数组我们也称之为矩阵,即:数组中的每一个元素为一个矩阵。如矩阵a:
a[3][3]={{1,2,2}{5,5,9}{8,9,7}}
矩阵的压缩存储
压缩存储是指多个值相同的元素只分配一个存储空间,对零元素不分配存储空间。 所以对于一般的矩阵我们是无法实现压缩存储的,我们今天看看特殊矩阵的压缩存储。
特殊矩阵:指具有许多相同矩阵元素或零元素,并且这些相同矩阵元素或零元素的分布有一定规律性的矩阵。
特殊矩阵的压缩存储:找出特殊矩阵中值相同的矩阵元素的分布规律,把那些呈现规律性分布、值相同的多个矩阵元素压缩存储到一个存储空间上。
今天我们看看常见的特殊矩阵的压缩存储分别是:对称矩阵,三角矩阵和三对角矩阵。
对称矩阵
若对一个n阶方阵A[1…n][1…n]中的任意元素a[i][j]都有a[i][j]=a[j][i] (1≤i,j≤n),则称其为对称矩阵,如下
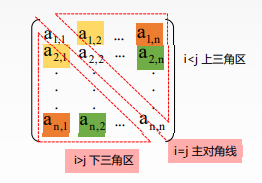
储存数组:A[n(n+1)/2]
数组下标k的计算:
i≥j时:
k=i(i-1)/2 + j-1
i<j时:
k=j(j-1)/2 + i-1
三角矩阵
三角矩阵 若对一个n阶方阵A[1…n][1…n]中上(下)三角区元素均为同一常量,则称为下 (上)三角矩阵。如:
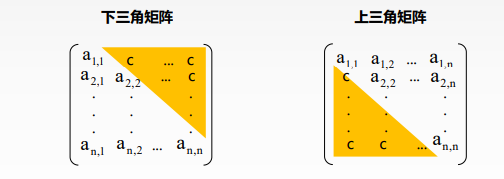
储存数组:A[n(n+1)/2+1]
数组下标k的计算(把常数存放在最后一个位置):
i≥j时:
k= i(i-1)/2 + j-1
i<j时:
k=n(n+1)/2
三对角矩阵
三对角矩阵 若对一个n阶方阵A中的任意元素a[i][j] ,当|i - j|>1,有 a[i][j]= 0(1≤i,j≤n),则 称为三对角矩阵。如下:
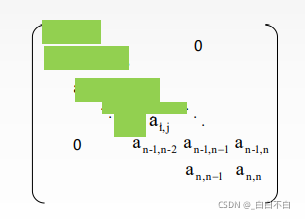
数组下标k的计算:
k = 2i+j-3
已知k求i与j
i = (k+1)/3+1
j = k-2i+3
稀疏矩阵
稀疏矩阵 矩阵元素个数s相对于矩阵中非零元素的个数t来说非常多,即s>>t的矩阵称为稀疏矩阵。对于稀疏矩阵我们一般使用三元组储存。
三元组一般是(i,j,value)
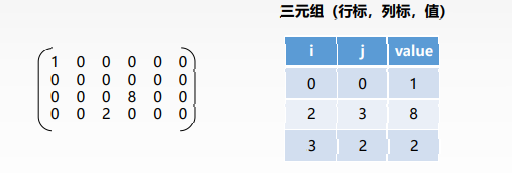
缺点:稀疏矩阵压缩存储后失去了随机存储的特性
结语
对于kmp算法还是蛮重要的,以后做算法题很容易遇到,大家好好理解,不要因为一时看不懂而直接放弃。
有问题请指教,多谢支持!
持续更新中…